ベイズ最適化を使用したモデル選択の自動化への移行

この例では次を使用します。

この例では、特定の学習データセットに対する複数の分類モデルをビルドし、ベイズ最適化を使用してそれらのハイパーパラメーターを最適化して、テストデータセットでの性能が最適なモデルを選択する方法を示します。

複数のモデルに学習させてそれらのハイパーパラメーターを調整するには、多くの場合、数日間または数週間かかります。複数のモデルを自動的に開発および比較するスクリプトを作成するほうが、より高速になり得ます。ベイズ最適化を使用してプロセスを高速化することもできます。異なるハイパーパラメーターのセットで各モデルに学習させる代わりに、少数の異なるモデルを選択し、ベイズ最適化を使用してそれらの既定のハイパーパラメーターを調整します。ベイズ最適化は、モデルの目的関数を最小化することにより特定のモデルに対するハイパーパラメーターの最適なセットを求めます。この最適化アルゴリズムは反復ごとに新しいハイパーパラメーターを戦略的に選択し、通常は、単純なグリッド探索よりも短時間で最適なハイパーパラメーターのセットに到達します。この例のスクリプトを使用すると、特定の学習データセットについてベイズ最適化を使用して複数の分類モデルに学習させ、テストデータセットでの性能が最適なモデルを特定できます。

あるいは、選択した分類器のタイプとハイパーパラメーターの値において自動的に分類モデルを選択するには、fitcauto を使用します。たとえば、ベイズ最適化および ASHA 最適化による分類器の自動選択を参照してください。

標本データの読み込み

この例では census1994.mat に保存されている 1994 年の国勢調査データを使用します。このデータセットは、個人の年収が $50,000 を超えるかどうかを予測するための、米国勢調査局の人口統計データから構成されます。この分類タスクでは、年齢、労働階級、教育レベル、婚姻区分、人種などが与えられた人の給与カテゴリを予測するモデルを当てはめます。

標本データ census1994 を読み込み、データセットの変数を表示します。

load census1994
whos

  Name                 Size              Bytes  Class    Attributes

  Description         20x74               2960  char               
  adultdata        32561x15            1872566  table              
  adulttest        16281x15             944466  table

census1994 には学習データセット adultdata およびテストデータセット adulttest が含まれています。この例では、実行時間を短縮するために、関数 datasample を使用して元の table adultdata および adulttest からそれぞれ 5000 の学習観測値とテスト観測値をサブサンプリングします (完全なデータセットを使用する場合は、この手順を省略できます)。

NumSamples = 5000;
s = RandStream('mlfg6331_64'); % For reproducibility
adultdata = datasample(s,adultdata,NumSamples,'Replace',false);
adulttest = datasample(s,adulttest,NumSamples,'Replace',false);

学習データセットの最初の数行をプレビューします。

head(adultdata)

    age     workClass       fnlwgt       education      education_num      marital_status         occupation         relationship     race      sex      capital_gain    capital_loss    hours_per_week    native_country    salary
    ___    ___________    __________    ____________    _____________    __________________    _________________    ______________    _____    ______    ____________    ____________    ______________    ______________    ______

    39     Private          4.91e+05    Bachelors            13          Never-married         Exec-managerial      Other-relative    Black    Male           0               0                45          United-States     <=50K 
    25     Private        2.2022e+05    11th                  7          Never-married         Handlers-cleaners    Own-child         White    Male           0               0                45          United-States     <=50K 
    24     Private        2.2761e+05    10th                  6          Divorced              Handlers-cleaners    Unmarried         White    Female         0               0                58          United-States     <=50K 
    51     Private        1.7329e+05    HS-grad               9          Divorced              Other-service        Not-in-family     White    Female         0               0                40          United-States     <=50K 
    54     Private        2.8029e+05    Some-college         10          Married-civ-spouse    Sales                Husband           White    Male           0               0                32          United-States     <=50K 
    53     Federal-gov         39643    HS-grad               9          Widowed               Exec-managerial      Not-in-family     White    Female         0               0                58          United-States     <=50K 
    52     Private             81859    HS-grad               9          Married-civ-spouse    Machine-op-inspct    Husband           White    Male           0               0                48          United-States     >50K  
    37     Private        1.2429e+05    Some-college         10          Married-civ-spouse    Adm-clerical         Husband           White    Male           0               0                50          United-States     <=50K

各行は、年齢、教育、職業など、成人 1 人の属性を表します。最後の列 salary は個人の年収が $50,000 以下か、$50,000 を超えるかどうかを示します。

データの理解および分類モデルの選択

Statistics and Machine Learning Toolbox™ には、分類木、判別分析、単純ベイズ、最近傍、サポートベクターマシン (SVM)、アンサンブル分類を含む、分類用の複数のオプションが用意されています。アルゴリズムの完全なリストについては、分類を参照してください。

問題に使用するアルゴリズムを選択する前に、データセットを検査します。国勢調査データには注目すべき複数の特性があります。

データは表形式であり、数値変数とカテゴリカル変数が両方含まれています。
データには欠損値が含まれています。
応答変数 (salary) には、2 つのクラス (バイナリ分類) があります。

何かを仮定したり、データで十分に機能することが予測されるアルゴリズムの事前知識を使用しないで、単純に表形式のデータとバイナリ分類をサポートするすべてのアルゴリズムに学習させます。誤り訂正出力符号 (ECOC) モデルは 3 つ以上のクラスがあるデータで使用されます。判別分析アルゴリズムおよび最近傍アルゴリズムは数値変数とカテゴリカル変数の両方が含まれるデータを解析しません。したがって、この例に適したアルゴリズムは、SVM、決定木、決定木のアンサンブル、および単純ベイズモデルです。これらのモデルの中には、決定木モデルや単純ベイズモデルなど、欠損値があるデータの扱いに優れたものもあります。つまり、欠損値がある観測値について NaN でない予測スコアを返します。

モデルのビルドおよびハイパーパラメーターの調整

プロセスを高速化するために、ハイパーパラメーター最適化オプションをカスタマイズします。'ShowPlots' を false として、'Verbose' を 0 として指定し、プロットの表示とメッセージの表示をそれぞれ無効にします。また、'UseParallel' を true として指定してベイズ最適化を並列実行しますが、これには Parallel Computing Toolbox™ が必要です。並列でのタイミングに再現性がないため、並列ベイズ最適化で再現性のある結果が生成されるとは限りません。

hypopts = struct('ShowPlots',false,'Verbose',0,'UseParallel',true);

並列プールを起動します。

poolobj = gcp;

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 8 workers.

各近似関数を呼び出して、その名前と値のペアの引数 'OptimizeHyperparameters' を 'auto' に設定することにより、学習データセットを近似し、パラメーターを簡単に調整できます。分類モデルを作成します。

% SVMs: SVM with polynomial kernel & SVM with Gaussian kernel
mdls{1} = fitcsvm(adultdata,'salary','KernelFunction','polynomial','Standardize','on', ...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts);
mdls{2} = fitcsvm(adultdata,'salary','KernelFunction','gaussian','Standardize','on', ...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts);

% Decision tree
mdls{3} = fitctree(adultdata,'salary', ...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts);

% Ensemble of Decision trees
mdls{4} = fitcensemble(adultdata,'salary','Learners','tree', ...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts);

% Naive Bayes
mdls{5} = fitcnb(adultdata,'salary', ...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions', hypopts);

目的曲線の最小値のプロット

ベイズ最適化の結果を各モデルから抽出し、ハイパーパラメーターの最適化の反復ごとに各モデルで観測された目的関数の最小値をプロットします。この目的関数値は学習データセットを使用した 5 分割交差検証で測定される誤分類率に対応します。プロットはモデルごとの性能を比較します。

figure
hold on
N = length(mdls);
for i = 1:N
    mdl = mdls{i};
    results = mdls{i}.HyperparameterOptimizationResults;
    plot(results.ObjectiveMinimumTrace,'Marker','o','MarkerSize',5);
end
names = {'SVM-Polynomial','SVM-Gaussian','Decision Tree','Ensemble-Trees','Naive Bayes'};
legend(names,'Location','northeast')
title('Bayesian Optimization')
xlabel('Number of Iterations')
ylabel('Minimum Objective Value')

Figure contains an axes object. The axes object with title Bayesian Optimization, xlabel Number of Iterations, ylabel Minimum Objective Value contains 5 objects of type line. These objects represent SVM-Polynomial, SVM-Gaussian, Decision Tree, Ensemble-Trees, Naive Bayes.

ベイズ最適化を使用してより適切なハイパーパラメーターセットを求めると、複数の反復にわたりモデルの性能が向上します。この場合、プロットは決定木のアンサンブルにデータの最高の予測精度があることを示しています。このモデルは、複数回の反復および異なるベイズ最適化のハイパーパラメーターのセットにわたり、一貫して適切に機能します。

テストセットによる性能のチェック

混同行列および受信者動作特性 (ROC) 曲線を使用して、テストデータセットで分類器の性能をチェックします。

テストデータセットの予測したラベルおよびスコア値を見つけます。

label = cell(N,1);
score = cell(N,1);
for i = 1:N
    [label{i},score{i}] = predict(mdls{i},adulttest);
end

混同行列

各モデルの関数 predict を使用して、テスト観測値ごとに最も可能性の高いクラスを取得します。次に、関数 confusionchart を使用して、テストデータセットの予測したクラスおよび既知の (true) クラスをもつ混同行列を計算します。

figure
c = cell(N,1);
for i = 1:N
    subplot(2,3,i)
    c{i} = confusionchart(adulttest.salary,label{i});
    title(names{i})
end

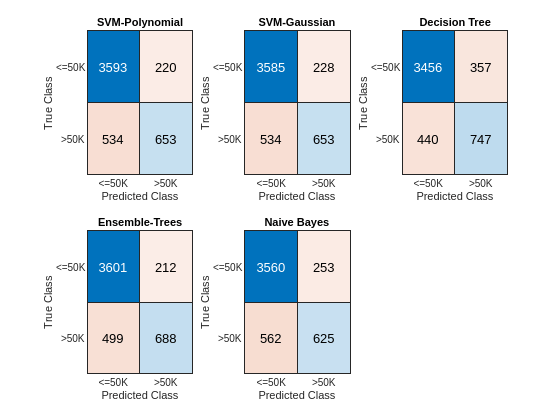
Figure contains objects of type ConfusionMatrixChart. The chart of type ConfusionMatrixChart has title SVM-Polynomial. The chart of type ConfusionMatrixChart has title SVM-Gaussian. The chart of type ConfusionMatrixChart has title Decision Tree. The chart of type ConfusionMatrixChart has title Ensemble-Trees. The chart of type ConfusionMatrixChart has title Naive Bayes.

対角要素は、特定のクラスの正しく分類されたインスタンスの数を示しています。非対角要素は誤分類した観測値のインスタンスです。

ROC 曲線

各分類器の ROC 曲線をプロットし、ROC 曲線の下の領域 (AUC) を計算することにより、より精密に分類器の性能を検査します。ROC 曲線は、分類スコアのさまざまなしきい値についての真陽性率と偽陽性率の関係を示します。しきい値にかかわらず真陽性率が常に 1 の完璧な分類器では、AUC = 1 になります。観測値をランダムにクラスに割り当てるバイナリ分類器では、AUC = 0.5 になります。大きな AUC 値 (1 に近い) は、分類器の性能が高いことを示します。

各分類器のrocmetricsオブジェクトを作成し、ROC 曲線のメトリクスを計算して AUC の値を求めます。rocmetrics の関数 plot を使用して、ラベル '<=50K' の ROC 曲線をプロットします。

figure
AUC = zeros(1,N);
for i = 1:N
    rocObj = rocmetrics(adulttest.salary,score{i},mdls{i}.ClassNames);
    [r,g] = plot(rocObj,'ClassNames','<=50K');
    r.DisplayName = replace(r.DisplayName,'<=50K',names{i});
    g(1).DisplayName = join([names{i},' Model Operating Point']);
    AUC(i) = rocObj.AUC(1);
    hold on
end
title('ROC Curves for Class <=50K')
hold off

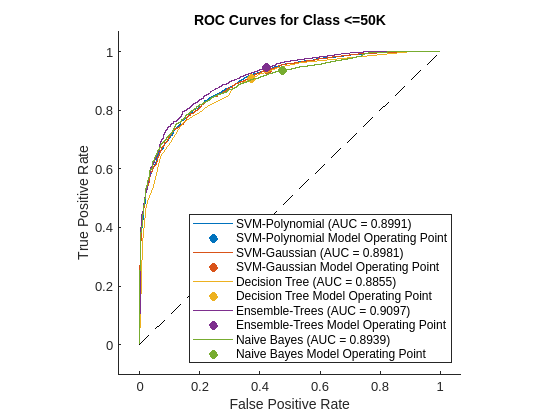
ROC 曲線は、分類器の出力のさまざまなしきい値についての真陽性率と偽陽性率の関係 (すなわち、感度対 1 - 特異度) を示します。

棒グラフを使用して AUC 値をプロットします。しきい値にかかわらず真陽性率が常に 1 の完璧な分類器では AUC = 1 になります。観測値を無作為にクラスに割り当てる分類器では、AUC = 0.5 になります。AUC の値が大きい場合、分類器の性能が高いことを示します。

figure
bar(AUC)
title('Area Under the Curve')
xlabel('Model')
ylabel('AUC')
xticklabels(names)
xtickangle(30)
ylim([0.85,0.925])

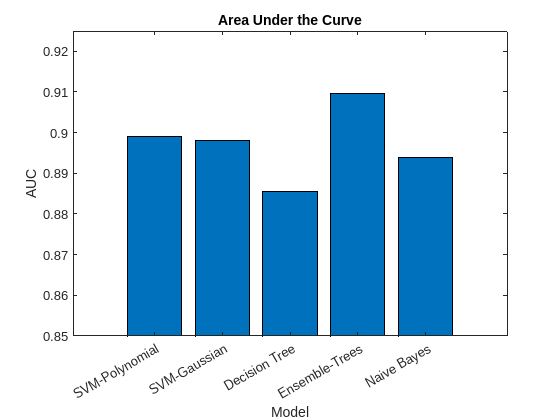
Figure contains an axes object. The axes object with title Area Under the Curve, xlabel Model, ylabel AUC contains an object of type bar.

混同行列および AUC の棒グラフに基づくと、決定木のアンサンブルと SVM モデルでは決定木モデルと単純ベイズモデルより高い精度が得られます。

最も有望なモデルの最適化の再開

さらなる反復にわたりすべてのモデルでベイズ最適化を実行すると、計算量が増大する場合があります。代わりに、これまで適切に機能したモデルのサブセットを選択し、関数resumeを使用してさらに 30 回の反復にわたり最適化を続けます。ベイズ最適化の反復ごとに観測された目的関数の最小値をプロットします。

figure
hold on
selectedMdls = mdls([1,2,4]);
newresults = cell(1,length(selectedMdls));
for i = 1:length(selectedMdls)
    newresults{i} = resume(selectedMdls{i}.HyperparameterOptimizationResults,'MaxObjectiveEvaluations',30);
    plot(newresults{i}.ObjectiveMinimumTrace,'Marker','o','MarkerSize',5)
end
title('Bayesian Optimization with resume')
xlabel('Number of Iterations')
ylabel('Minimum Objective Value')
legend({'SVM-Polynomial','SVM-Gaussian','Ensemble-Trees'},'Location','northeast')

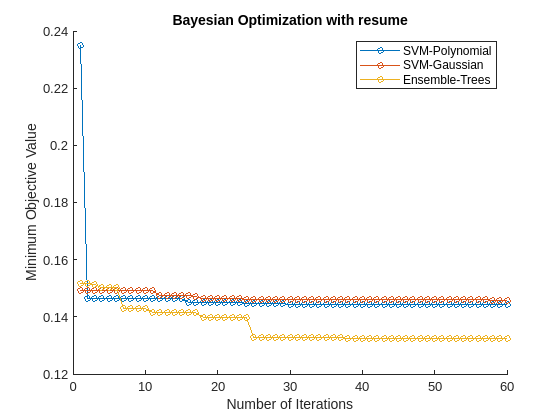
Figure contains an axes object. The axes object with title Bayesian Optimization with resume, xlabel Number of Iterations, ylabel Minimum Objective Value contains 3 objects of type line. These objects represent SVM-Polynomial, SVM-Gaussian, Ensemble-Trees.