部分最小二乗

部分最小二乗の紹介

"部分最小二乗" ("PLS") 回帰は、相関関係がある複数の予測子変数が含まれているデータに対して使用される手法です。この手法は、元の予測子変数の線形結合として、"成分" として知られる、新しい予測子変数を構成します。部分最小二乗は、観測された応答値を考慮しつつ、これらの成分を構成し、信頼できる予測力をもつ単純なモデルを作成します。

この手法は、多重線形回帰 と 主成分分析の中間と言えるでしょう。

• 多重線形回帰は、応答に最もよく適合する予測子の組み合わせを見つけます。

• 主成分分析は、大きな分散で予測子の組み合わせを見つけ、相関関係を減らします。この手法では応答値は使用されません。

• 部分最小二乗は、大きい共分散をもつ予測子の組み合わせを応答値で見つけます。

したがって、部分最小二乗は、それらの相関関係も考慮しながら、予測子と応答の両方の分散に関する情報を結合します。

部分最小二乗は、他の回帰と特徴変換手法の特徴を共有します。相関予測子をもつ状況で使用されるという点で、これはリッジ回帰に似ています。モデル項のより小さいセットを選択するために使用できるという点で、ステップワイズ回帰 (または、より一般的な特徴選択手法) にも似ています。しかし、部分最小二乗がこれらのメソッドと異なるのは、元の予測子空間を新しい成分の空間に変換することです。

関数 plsregress は、PLS 回帰を行います。

部分最小二乗回帰の実行

この例では、部分最小二乗回帰を実行する方法と部分最小二乗モデルの成分の数を選ぶ方法を示します。

相関関係を導入するために予測子のノイズ バージョンが付加される moore.mat 内の生物化学的酸素要求量のデータを考えてみましょう。

load moore
y = moore(:,6);              % Response
X0 = moore(:,1:5);           % Original predictors
X1 = X0+10*randn(size(X0));  % Correlated predictors
X = [X0,X1];

plsregressを使用して、予測子と同じ数の成分によって部分最小二乗回帰を実行します。次に、成分数の関数として応答で説明されるパーセンテージ分散をプロットします。

[XL,yl,XS,YS,beta,PCTVAR] = plsregress(X,y,10);
plot(1:10,cumsum(100*PCTVAR(2,:)),'-o')
xlabel('Number of PLS components')
ylabel('Percent Variance Explained in y')

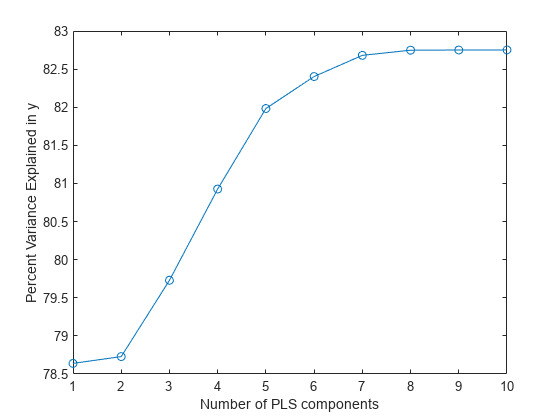
部分最小二乗モデルの成分の数を選ぶステップは重要です。プロットはおおよその情報を与え、最初の成分によって説明される y の分散の約 80% を示します。最大 5 つの追加成分が非常に役立ちます。

以下は 6 成分のモデルを計算します。

[XL,yl,XS,YS,beta,PCTVAR,MSE,stats] = plsregress(X,y,6);
yfit = [ones(size(X,1),1) X]*beta;
plot(y,yfit,'o')

散布は、当てはめた応答と観測応答の妥当な相関関係を示します。これは、${\mathit{R}}^2$ の統計量によって確認されます。

TSS = sum((y-mean(y)).^2);
RSS = sum((y-yfit).^2);
Rsquared = 1 - RSS/TSS

Rsquared = 
0.8240

個々の 6 成分における 10 個の予測子の重み付けしたプロットは、2 つの成分 (最後に計算された 2 つ) が X において分散の大多数を説明することを示します。

figure
plot(1:10,stats.W,'o-')
legend({'c1','c2','c3','c4','c5','c6'},'Location','best')
xlabel('Predictor')
ylabel('Weight')

平均二乗誤差のプロットは、少なくとも 2 つの成分が適正なモデルを提供することを示唆します。

figure
yyaxis left
plot(0:6,MSE(1,:),'-o')
yyaxis right
plot(0:6,MSE(2,:),'-o')
legend('MSE Predictors','MSE Response')
xlabel('Number of Components')

plsregress による平均二乗誤差の計算は、交差検証のタイプとモンテカルロ反復の数を指定するオプションの名前と値の引数により制御されます。

参考

plsregress

関連するトピック

• 部分最小二乗回帰と主成分回帰