リッジ回帰
リッジ回帰の紹介
線形回帰で説明するモデルの係数の推定は、モデルの項の独立性に依存します。項が相関しており、計画行列 X の列がほぼ線形依存関係をもつ場合、行列 (XTX)–1 は特異行列に近づきます。結果として、最小二乗推定
は、分散を大きくし、観測された応答 y の確率的誤差への感度が高くなります。このような状況は "多重共線性" と呼ばれ、実験計画を立てずにデータを収集した場合などに発生します。
リッジ回帰は、以下を使って回帰係数を推定することによって問題に対応します。
ここで、k は "リッジ パラメーター"、I は単位行列です。小さな正の値の k は、問題の調整を改善し、推定の分散を小さくします。偏りはありますが、リッジ推定の分散が小さくなると、多くの場合に最小二乗推定より平均二乗誤差が小さくなります。
Statistics and Machine Learning Toolbox™ の関数 ridge は、リッジ回帰を行います。
リッジ回帰
この例では、リッジ回帰を実行する方法を示します。
予測子変数 x1、x2 および x3 の観測値と応答変数 y が含まれている acetylene.mat のデータを読み込みます。
load acetylene予測子変数を他の予測子変数に対してプロットします。
subplot(1,3,1) plot(x1,x2,'.') xlabel('x1') ylabel('x2') grid on axis square subplot(1,3,2) plot(x1,x3,'.') xlabel('x1') ylabel('x3') grid on axis square subplot(1,3,3) plot(x2,x3,'.') xlabel('x2') ylabel('x3') grid on axis square
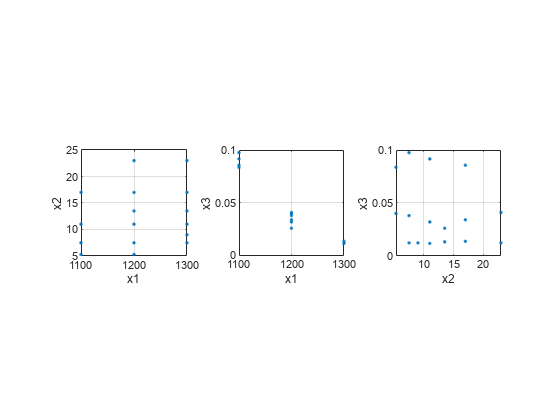
x1 と他の 2 つの予測子変数の相関に注意します。
ridge と x2fx を使用して、リッジ パラメーターの範囲に対して、交互作用項がある多重線形モデルの係数の推定を計算します。
X = [x1 x2 x3]; D = x2fx(X,'interaction'); D(:,1) = []; % No constant term k = 0:1e-5:5e-3; betahat = ridge(y,D,k);
リッジのトレースをプロットします。
figure plot(k,betahat,'LineWidth',2) ylim([-100 100]) grid on xlabel('Ridge Parameter') ylabel('Standardized Coefficient') title('{\bf Ridge Trace}') legend('x1','x2','x3','x1x2','x1x3','x2x3')
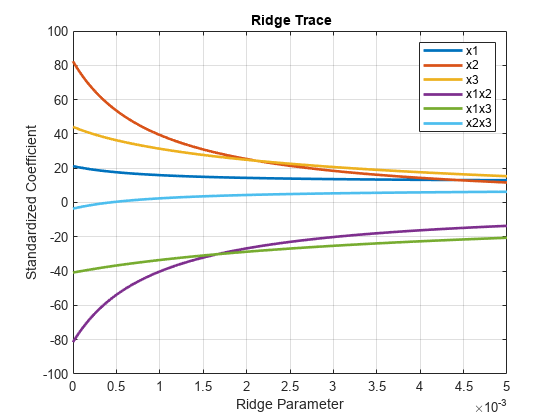
この推定は、プロットの右において一定になります。リッジ パラメーターの値が になると交互作用項 x2x3 の係数の符号が変わることに注意してください。
参考
lasso | lassoglm | fitrlinear | lassoPlot | ridge