Main Content

LASSO 正則化

ライブ スクリプトを開く

この例では、lasso で不要な予測子を識別して破棄する方法を示します。

さまざまな手段により、5 次元の人為的なデータ X の標本を指数分布から 200 個生成します。

rng(3,'twister') % For reproducibility
X = zeros(200,5);
for ii = 1:5
    X(:,ii) = exprnd(ii,200,1);
end

応答データ Y = X * r + eps を生成します。r には非ゼロ成分が 2 つしかなく、ノイズ eps は標準偏差が 0.1 の正規分布に従います。

r = [0;2;0;-3;0];
Y = X*r + randn(200,1)*.1;

交差検証されたモデルのシーケンスを lasso で当てはめ、結果をプロットします。

[b,fitinfo] = lasso(X,Y,'CV',10);
lassoPlot(b,fitinfo,'PlotType','Lambda','XScale','log');

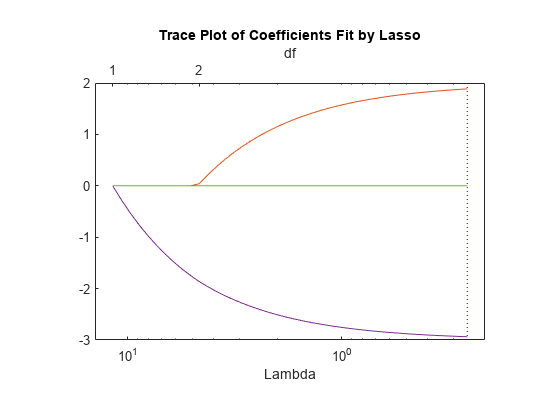
MATLAB figure

このプロットには、Lambda 正則化パラメーターのさまざまな値に対する回帰での非ゼロの係数が表示されます。Lambda の大きな値はグラフの左側に表示され、より正則化されると、非ゼロの回帰係数が少なくなることを意味します。

縦の点線は、最小平均二乗誤差が発生した Lambda 値 (右側) と、最小平均二乗誤差に 1 つの標準偏差を加算した Lambda 値を表します。この後者の値は、Lambda の推奨設定です。これらの線は交差検証を実行する場合にのみ表示されます。名前と値のペアの引数 'CV' を設定することにより交差検証を行います。この例では、10 分割交差検証を使用しています。

プロットの上部には自由度 (df) が表示され、回帰内の非ゼロの係数の数を Lambda の関数として示します。左側では、Lambda 値が大きいため、1 つを除くすべての係数が 0 になっています。右側では、5 つの係数はすべて非ゼロですが、2 つの係数だけがプロットに明確に示されています。他の 3 つの係数は非常に小さいので、視覚的に 0 と区別できません。

Lambda の値が小さい場合 (プロットの右方向)、係数の値は最小二乗の推定値に近づきます。

最小交差検証平均二乗誤差に 1 標準偏差を加えた Lambda 値を見つけます。この Lambda で、当てはめの MSE および係数を調べます。

lam = fitinfo.Index1SE;
fitinfo.MSE(lam)
ans = 0.1398

b(:,lam)
ans = 5×1

         0
    1.8855
         0
   -2.9367
         0

lasso は、係数ベクトル r を適切に検出しました。

比較のため、r の最小二乗推定値を求めます。

rhat = X\Y
rhat = 5×1

   -0.0038
    1.9952
    0.0014
   -2.9993
    0.0031

推定値 b(:,lam) では、rhat の平均二乗誤差よりも平均二乗誤差がわずかに大きくなります。

res = X*rhat - Y;     % Calculate residuals
MSEmin = res'*res/200 % b(:,lam) value is 0.1398
MSEmin = 0.0088

しかし、b(:,lam) に含まれる非ゼロの成分は 2 つのみであるため、新しいデータでより適切な予測推定を提示できます。

参考

| | | |

関連するトピック