データの探索的解析
可視化と記述統計を使用してデータの分布を調べます。結果を正規分布と比較します。
データの生成
無作為に生成された標本データを含むベクトルを生成します。平均が 4 で標準偏差が 1 の正規分布から生成される 100 個の乱数と、平均が 6 で標準偏差が 0.5 の正規分布から生成される 200 個の乱数を組み合わせます。
rng(0,"twister") % For reproducibility x = [normrnd(4,1,1,100),normrnd(6,0.5,1,200)];
データの可視化
標本データのヒストグラムを正規密度の近似とともにプロットします。このプロットにより、データに当てはめた正規分布と標本データを視覚的に比較できます。
histfit(x)
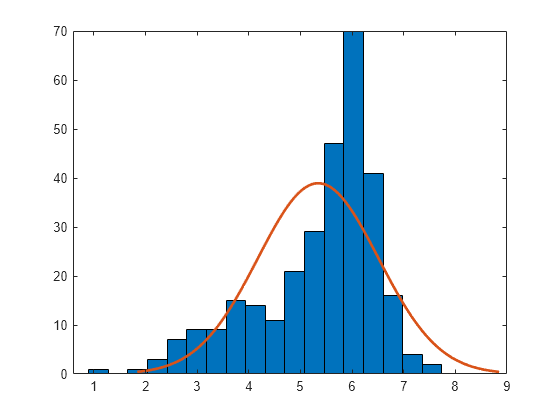
データの分布は歪んでおり、左の裾が長くなっているように見えます。正規分布は、この標本データに適した近似ではないようです。
正規確率プロットを作成します。このプロットは、データに当てはめた正規分布と標本データを視覚的に比較するための別の方法を提供します。
probplot("normal",x)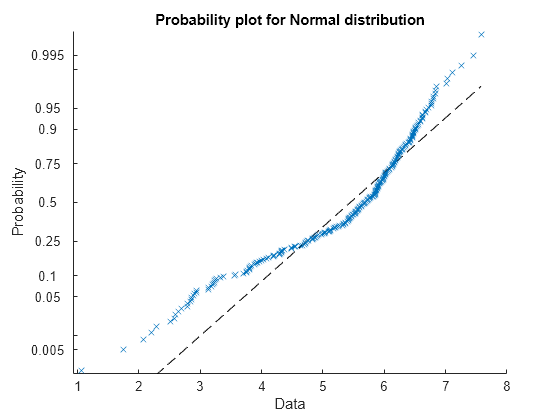
プロットされた点が基準線に沿っていないように見えることから、この確率プロットもデータが正規性から逸脱していることを示しています。
箱ひげ図を作成して統計量を可視化します。
boxchart(x)
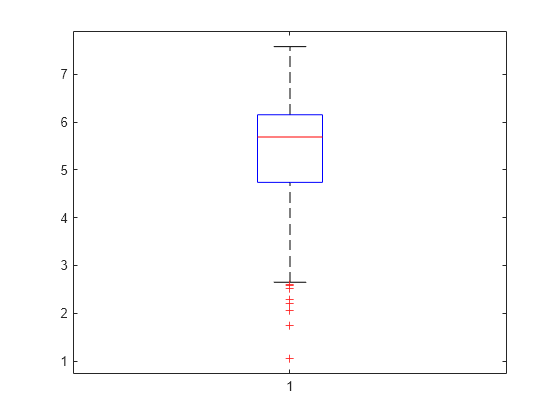
箱ひげ図には、0.25、0.5 および 0.75 の分位数が示されます。ボックスの内側の線は 0.5 分位数 (中央値) に対応し、ボックスの上下の端はそれぞれ 0.25 と 0.75 の分位数に対応します。長い下裾と円で囲まれた点 (外れ値) は、標本データの値に対称性が欠けていることを示しています。
記述統計の計算
データの平均値と中央値を計算します。
y1 = [mean(x),median(x)]
y1 = 1×2
5.3438 5.6872
平均値と中央値は近いように見えますが、平均値が中央値より小さい場合、通常はデータが歪んでいて左の裾が長くなっています。
データの歪度と尖度を計算します。
y2 = [skewness(x),kurtosis(x)]
y2 = 1×2
-1.0417 3.5895
歪度の値が負の場合、データは左に歪んでいることを意味します。尖度の値が 3 より大きいため、データの尖度は正規分布より大きくなります。
z スコアを計算し、3 より大きいか -3 より小さい値を探すことにより、外れ値の可能性がある値を識別します。
z = zscore(x); find(abs(z)>3)
ans = 1×2
3 35
z スコアに基づくと、3 番目の観測値と 35 番目の観測値は外れ値の可能性があります。
参考
boxchart | histfit | probplot | mean | median | quantile | skewness | kurtosis | zscore | boxplot