confusionmat

分類問題用の混同行列の計算

構文

C = confusionmat(group,grouphat)

C = confusionmat(group,grouphat,'Order',grouporder)

[C,order] = confusionmat(___)

説明

C = confusionmat(group,grouphat) は、既知のグループ group と予測されたグループ grouphat によって決定される混同行列 C を返します。

C = confusionmat(group,grouphat,'Order',grouporder) は、grouporder を使用して C の行と列の順序を設定します。

[C,order] = confusionmat(___) は、前の構文の入力引数のいずれかを使用して、変数 order に C の行と列の順序も返します。

例

混同行列の表示

2 つの誤分類と 1 つの欠損分類が含まれているデータについて混同行列を表示します。

既知のグループと予測されたグループについてベクトルを作成します。

g1 = [3 2 2 3 1 1]';	% Known groups
g2 = [4 2 3 NaN 1 1]';	% Predicted groups

混同行列を取得します。

C = confusionmat(g1,g2)

C = 4×4

     2     0     0     0
     0     1     1     0
     0     0     0     1
     0     0     0     0

混同行列 C の行と列のインデックスは同一であり、既定では [g1;g2] の並べ替え順序で編成されます。つまり、(1,2,3,4) になります。

この混同行列は、グループ 1 に属することがわかっている 2 つのデータ点が正しく分類されたことを示しています。グループ 2 については、1 つのデータ点がグループ 3 として誤分類されています。また、グループ 3 に属することがわかっているデータ点の 1 つがグループ 4 として誤分類されています。confusionmat は、グループ化変数 g2 内の NaN 値を欠損値として処理し、C の行と列には含めません。

confusionchart を使用して、混同行列を混同行列チャートとしてプロットします。

confusionchart(C)

プロットする前に混同行列を計算する必要はありません。代わりに、confusionchart を使用して、真のラベルと予測ラベルから混同行列チャートを直接プロットします。

cm = confusionchart(g1,g2)

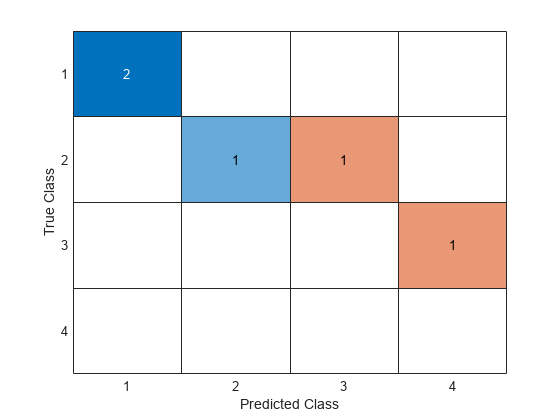
cm = 
  ConfusionMatrixChart with properties:

    NormalizedValues: [4x4 double]
         ClassLabels: [4x1 double]

  Use GET to show all properties

ConfusionMatrixChart オブジェクトでは、数値混同行列が NormalizedValues プロパティに、クラスが ClassLabels プロパティに格納されます。ドット表記を使用して、これらのプロパティを表示します。

cm.NormalizedValues

ans = 4×4

     2     0     0     0
     0     1     1     0
     0     0     0     1
     0     0     0     0

cm.ClassLabels

ans = 4×1

     1
     2
     3
     4

混同行列のグループ順序の指定

2 つの誤分類と 1 つの欠損分類が含まれているデータについて混同行列を表示し、グループの順序を指定します。

既知のグループと予測されたグループについてベクトルを作成します。

g1 = [3 2 2 3 1 1]';	% Known groups
g2 = [4 2 3 NaN 1 1]';	% Predicted groups

グループの順序を指定し、混同行列を取得します。

C = confusionmat(g1,g2,'Order',[4 3 2 1])

C = 4×4

     0     0     0     0
     1     0     0     0
     0     1     1     0
     0     0     0     2

混同行列 C の行と列のインデックスは同じであり、グループの順序で指定された順序で編成されます。つまり、(4,3,2,1) になります。

混同行列 C の 2 行目は、グループ 3 に属することがわかっているデータ点の 1 つがグループ 4 として誤分類されたことを示しています。C の 3 行目は、グループ 2 に属しているデータ点の 1 つがグループ 3 として誤分類されたことを示し、4 行目は、グループ 1 に属することがわかっている 2 つのデータ点が正しく分類されたことを示しています。confusionmat は、グループ化変数 g2 内の NaN 値を欠損値として処理し、C の行と列には含めません。

分類用の混同行列

fisheriris データ セットの標本に対して分類を実行し、生成された結果について混同行列を表示します。

フィッシャーのアヤメのデータ セットを読み込みます。

load fisheriris

データ内の測定値とグループをランダム化します。

rng(0,'twister'); % For reproducibility
numObs = length(species);
p = randperm(numObs);
meas = meas(p,:);
species = species(p);

データの最初の半分に含まれている測定値を使用して、判別分析分類器に学習をさせます。

half = floor(numObs/2);
training = meas(1:half,:);
trainingSpecies = species(1:half);
Mdl = fitcdiscr(training,trainingSpecies);

学習済みの分類器を使用して、データの後半部分の測定値についてラベルを予測します。

sample = meas(half+1:end,:);
grouphat = predict(Mdl,sample);

グループの順序を指定し、生成された分類について混同行列を表示します。

group = species(half+1:end);
[C,order] = confusionmat(group,grouphat,'Order',{'setosa','versicolor','virginica'})

C = 3×3

    29     0     0
     0    22     2
     0     0    22

order = 3x1 cell
    {'setosa'    }
    {'versicolor'}
    {'virginica' }

この混同行列は、setosa および virginica に属している測定値が正しく分類され、versicolor に属している測定値の 2 つが virginica として誤分類されたことを示しています。出力 order には、グループ順序 {'setosa','versicolor','virginica'} で指定された順序で混同行列の行と列の順序が格納されます。

tall 配列を使用した分類用の混同行列

fisheriris データ セットの tall 配列に対して分類を実行し、関数 confusionmat を使用して既知および予測 tall ラベルについて混同行列を計算し、関数 confusionchart を使用して混同行列をプロットします。

tall 配列に対する計算を実行する場合、MATLAB® は並列プール (Parallel Computing Toolbox™ がある場合は既定) またはローカルの MATLAB セッションを使用します。Parallel Computing Toolbox がある場合でもローカルの MATLAB セッションを使用して例を実行するには、関数mapreducerを使用してグローバルな実行環境を変更できます。

フィッシャーのアヤメのデータ セットを読み込みます。

load fisheriris

インメモリ配列 meas および species を tall 配列に変換します。

tx = tall(meas);

Starting parallel pool (parpool) using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).

ty = tall(species);

tall 配列内の観測値の個数を求めます。

numObs = gather(length(ty));   % gather collects tall array into memory

再現性を得るために rng と tallrng を使用して乱数発生器のシードを設定し、学習標本を無作為に選択します。tall 配列の場合、ワーカーの個数と実行環境によって結果が異なる可能性があります。詳細については、コードの実行場所の制御を参照してください。

rng('default') 
tallrng('default')
numTrain = floor(numObs/2);
[txTrain,trIdx] = datasample(tx,numTrain,'Replace',false);
tyTrain = ty(trIdx); 

決定木分類器モデルを学習標本に当てはめます。

mdl = fitctree(txTrain,tyTrain); 

Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 2: Completed in 3.9 sec
- Pass 2 of 2: Completed in 1.5 sec
Evaluation completed in 7.3 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 4: Completed in 0.88 sec
- Pass 2 of 4: Completed in 1.6 sec
- Pass 3 of 4: Completed in 4 sec
- Pass 4 of 4: Completed in 2.7 sec
Evaluation completed in 11 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 4: Completed in 0.54 sec
- Pass 2 of 4: Completed in 1.2 sec
- Pass 3 of 4: Completed in 3 sec
- Pass 4 of 4: Completed in 2 sec
Evaluation completed in 7.6 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 4: Completed in 0.51 sec
- Pass 2 of 4: Completed in 1.3 sec
- Pass 3 of 4: Completed in 3.1 sec
- Pass 4 of 4: Completed in 2.5 sec
Evaluation completed in 8.5 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 4: Completed in 0.42 sec
- Pass 2 of 4: Completed in 1.2 sec
- Pass 3 of 4: Completed in 3 sec
- Pass 4 of 4: Completed in 2.1 sec
Evaluation completed in 7.6 sec

学習済みのモデルを使用して、テスト標本のラベルを予測します。

txTest = tx(~trIdx,:);
label = predict(mdl,txTest);

生成された分類について混同行列を計算します。

tyTest = ty(~trIdx);
[C,order] = confusionmat(tyTest,label)

C =

  M×N×... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.


order =

  M×N×... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

Preview deferred. Learn more.

関数 gather を使用して遅延計算を実行し、confusionmat の結果をメモリに返します。

gather(C)

Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 1: Completed in 1.9 sec
Evaluation completed in 2.3 sec

ans = 3×3

    20     0     0
     1    30     2
     0     0    22

gather(order)

Evaluating tall expression using the Parallel Pool 'local':
Evaluation completed in 0.032 sec

ans = 3×1 cell
    {'setosa'    }
    {'versicolor'}
    {'virginica' }

この混同行列は、versicolor クラスの測定値の 3 つが誤分類されたことを示しています。setosa および virginica に属している測定は、すべて正しく分類されています。

混同行列の計算とプロットを行うため、代わりにconfusionchartを使用します。

cm = confusionchart(tyTest,label)

Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 1: Completed in 0.34 sec
Evaluation completed in 0.6 sec
Evaluating tall expression using the Parallel Pool 'local':
- Pass 1 of 1: Completed in 0.48 sec
Evaluation completed in 0.67 sec

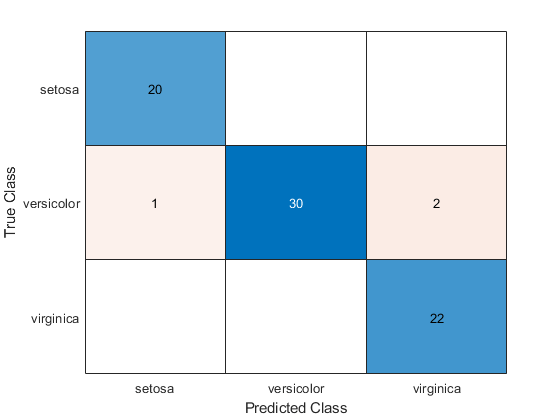
cm = 
  ConfusionMatrixChart with properties:

    NormalizedValues: [3×3 double]
         ClassLabels: {3×1 cell}

  Show all properties

頻度の行列の表示

関数 confusionmat を使用して、tall table の列にリストされた空港間を飛行するフライトの数を示す行列を作成します。

tall 配列に対する計算を実行する場合、MATLAB® は並列プール (Parallel Computing Toolbox™ がある場合は既定) またはローカルの MATLAB セッションを使用します。Parallel Computing Toolbox がある場合にローカルの MATLAB セッションを使用して例を実行するには、関数 mapreducer を使用してグローバルな実行環境を変更します。

mapreducer(0)

airlinesmall.csv データ セットのデータストアを作成します。NaN 値に置き換えられるように、'NA' 値を欠損データとして扱います。データストアに含める変数として Origin と Dest を選択します。

varnames = {'Origin','Dest'};
ds = datastore('airlinesmall.csv','TreatAsMissing','NA', ...
    'SelectedVariableNames',varnames);

データストアのデータの tall 配列を作成します。ds のデータは表形式であるため、結果は tall table になります。データが表形式でない場合は、代わりに tall cell 配列が tall で作成されます。

T = tall(ds)

T =

  Mx2 tall table

    Origin      Dest  
    _______    _______

    {'LAX'}    {'SJC'}
    {'SJC'}    {'BUR'}
    {'SAN'}    {'SMF'}
    {'BUR'}    {'SJC'}
    {'SMF'}    {'LAX'}
    {'LAX'}    {'SJC'}
    {'SAN'}    {'SFO'}
    {'SEA'}    {'LAX'}
       :          :
       :          :

tall table の表示は、データの行数が不明であることを示しています。

列 T.Origin と列 T.Dest の間のフライト数を示す行列を作成します。2 つの列に分類による既知の予測値が格納されていないため、この行列は混同行列ではありません。ただし、関数 confusionmat を使用して頻度の行列を作成できます。

[ta,tb] = confusionmat(T.Origin,T.Dest)

ta =

  MxNx... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :


tb =

  MxNx... tall array

    ?    ?    ?    ...
    ?    ?    ?    ...
    ?    ?    ?    ...
    :    :    :
    :    :    :

関数 gather を使用して遅延計算を実行し、confusionmat の結果をメモリに返します。

[freqMatrix,airportOrder] = gather(ta,tb);

Evaluating tall expression using the Local MATLAB Session:
- Pass 1 of 1: Completed in 2 sec
Evaluation completed in 2.6 sec

行列 freqMatrix の最初の 5 行、および対応する行と列の順序 airportOrder を表示します。

freqMatrix(1:5,:)

ans = 5×323

     0   153   169     0    91   161   322     0    44     6    56    24     0     0    23   180   122    20   150    20    63    77   134    37    10     0     3    51     0     1   311     0    15     0    32    81    30    53     0     9     2    15    12   293    20    38     1    73     0    41
   168     0    75    59     5    76     0     6    14    79     0     1     0     0     0    54    60     0     5     0     1     5    51     0     0     0     0     1     0     0    55     0     0     0     8    67    50     0     0     0     0    18     1    59     1     0     0    11     0     4
   187    87     0     0    78    39   120     0    14     1    18    19     0     0     0    98    95     2    19     3    14    14    72     0     0     0     0     0     0     0   108     0     1     0     1    31     4    14     0     1     0     3     9   172     5    13     0    21     0    10
     0    58     0     0    61    25    83     3     2     1     0     0     0     0     0     0    23     0     5     0     0     0    21     0     0     0     0     0     0     0    87     0     0     0     0    13     0     0     0     0     0     0     0    67     0     0     0     1     0     0
   114     1    88    73     0    70    20     5     4    47     1     3     0     0     0    40    39     0     1     0     0     3    57     0     0     0     0     0     0     0    50     0     1     0     1    28     1     0     0     0     0     0     2    58     5     0     0    21     0     0

airportOrder(1:5)

ans = 5x1 cell
    {'LAX'}
    {'SJC'}
    {'SAN'}
    {'BUR'}
    {'SMF'}

行列 freqMatrix には、出発空港 (行) から目的空港 (列) へのフライトの数が表示されます。たとえば、SJC を出発して LAX に到着するフライトの総数は 168 です (freqMatrix(2,1) を参照)。同様に、SMF を出発して SAN に到着するフライトは 88 です (freqMatrix(5,3) を参照)。前述のように、freqMatrix は混同行列ではありませんが、空港間のフライトの数を示します。出発空港と目的空港は常に異なるため、予想どおり、対角要素はすべてゼロになります。

入力引数

group — 既知のグループ

数値ベクトル | logical ベクトル | 文字配列 | string 配列 | 文字ベクトルの cell 配列 | categorical ベクトル

観測値を分類するための既知のグループ。数値ベクトル、logical ベクトル、文字配列、string 配列、文字ベクトルの cell 配列、または categorical ベクトルを指定します。

group は、grouphat と同じ型のグループ化変数です。グループ化変数で説明されているように、引数 group には grouphat と同じ個数の観測値が含まれていなければなりません。関数 confusionmat は、文字配列および string 配列を文字ベクトルの cell 配列として処理します。さらに confusionmat は、group 内の NaN、空および 'undefined' 値を欠損値として処理し、個別のグループまたはカテゴリとしてはカウントしません。

例: {'Male','Female','Female','Male','Female'}

データ型: single | double | logical | char | string | cell | categorical

grouphat — 予測されたグループ

数値ベクトル | logical ベクトル | 文字配列 | string 配列 | 文字ベクトルの cell 配列 | categorical ベクトル

観測値を分類するための予測されたグループ。数値ベクトル、logical ベクトル、文字配列、string 配列、文字ベクトルの cell 配列、または categorical ベクトルを指定します。

grouphat は、group と同じ型のグループ化変数です。グループ化変数で説明されているように、引数 grouphat には group と同じ個数の観測値が含まれていなければなりません。関数 confusionmat は、文字配列および string 配列を文字ベクトルの cell 配列として処理します。さらに confusionmat は、grouphat 内の NaN、空および 'undefined' 値を欠損値として処理し、個別のグループまたはカテゴリとしてはカウントしません。

例: [1 0 0 1 0]

データ型: single | double | logical | char | string | cell | categorical

grouporder — グループの順序

数値ベクトル | logical ベクトル | 文字配列 | string 配列 | 文字ベクトルの cell 配列 | categorical ベクトル

グループの順序。数値ベクトル、logical ベクトル、文字配列、string 配列、文字ベクトルの cell 配列、または categorical ベクトルを指定します。

grouporder は、group および grouphat 内の異なる要素がすべて含まれているグループ化変数です。C の行と列の順序を定義するには、grouporder を指定します。group にも grouphat にもない要素が grouporder に含まれている場合、C の対応するエントリは 0 になります。

既定では、グループの順序は s = [group;grouphat] のデータ型によって変化します。

• 数値および logical ベクトルの場合、s の並べ替え順序になります。

• categorical ベクトルの場合、categories(s) によって返される順序になります。

• 他のデータ型の場合、s に最初に現れた順序になります。

例: 'order',{'setosa','versicolor','virginica'}

データ型: single | double | logical | char | string | cell | categorical

出力引数

C — 混同行列

行列

混同行列。引数 group および grouphat 内の異なる要素の総数に等しいサイズをもつ正方行列として返されます。C(i,j) は、グループ i に属することがわかっているがグループ j に属すると予測された観測値の個数です。

C の行と列は、同じグループ インデックスについて同じ順序になります。既定では、グループの順序は s = [group;grouphat] のデータ型によって変化します。

• 数値および logical ベクトルの場合、s の並べ替え順序になります。

• categorical ベクトルの場合、categories(s) によって返される順序になります。

• 他のデータ型の場合、s に最初に現れた順序になります。

順序を変更するには、grouporder を指定します。

関数 confusionmat は、グループ化変数内の NaN、空および 'undefined' 値を欠損値として処理し、C の行と列には含めません。

order — 行と列の順序

数値ベクトル | logical ベクトル | categorical ベクトル | 文字ベクトルの cell 配列

C の行と列の順序。数値ベクトル、logical ベクトル、categorical ベクトル、または文字ベクトルの cell 配列として返されます。group および grouphat が文字配列、string 配列、または文字ベクトルの cell 配列である場合、変数 order は文字ベクトルの cell 配列になります。それ以外の場合、order は group および grouphat と同じ型になります。

代替機能

• 混同行列の計算とプロットを行うには、confusionchart を使用します。さらに confusionchart は、データに関する要約統計量を表示し、クラス単位の精度 (陽性の予測値)、クラス単位の再現率 (真陽性率)、または正しく分類された観測値の総数に従って混同行列のクラスを並べ替えます。

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

この関数は、tall 配列を完全にサポートします。詳細は、tall 配列を参照してください。

バージョン履歴

R2008b で導入

参考

categories | crosstab | confusionchart

トピック

• グループ化変数