resubLoss

分類木モデルの再代入分類損失

構文

L = resubLoss(tree)

L = resubLoss(tree,Name=Value)

[L,SE,Nleaf,BestLevel] = resubLoss(___)

説明

L = resubLoss(tree) は、tree.X に格納されている学習データと tree.Y に格納されている対応する真のクラス ラベルを使用して、学習済み分類木モデル tree の再代入による分類損失 L を返します。resubLoss で既定で使用される損失は、fitctree での tree の作成に使用されたデータについて計算された損失です。

分類損失 (L) は再代入の品質に対する尺度です。解釈は損失関数 (LossFun) によって異なりますが、一般に、優れた分類器の方が分類損失値が小さくなります。LossFun の既定値は "mincost" (最小予測誤分類コスト) です。

L = resubLoss(tree,Name=Value) では、1 つ以上の名前と値の引数を使用して追加オプションを指定します。たとえば、resubLoss が分類損失の計算に使用する損失関数、枝刈りレベル、木のサイズを指定できます。

[L,SE,Nleaf,BestLevel] = resubLoss(___) は、分類誤差の標準誤差、枝刈り順序の木に含まれる葉ノードの数、および名前と値の引数 TreeSize で定義される最適な枝刈りレベルも返します。既定では、BestLevel は、損失が最小損失の 1 標準偏差以内になる枝刈りレベルです。

例

標本内分類誤差の計算

ionosphere データについて、再代入分類誤差を計算します。

load ionosphere
tree = fitctree(X,Y);
L = resubLoss(tree)

L = 
0.0114

各部分木の分類誤差の確認

枝刈りをしていない決定木は、過適合になる傾向があります。モデルの複雑さと標本外性能のバランスをとる方法の 1 つとして、標本内性能と標本外性能が十分高くなるように木の枝刈りを行います (つまり木の成長を制限します)。

フィッシャーのアヤメのデータ セットを読み込みます。データを学習セット (50%) と検証セット (50%) に分割します。

load fisheriris
n = size(meas,1);
rng(1) % For reproducibility
idxTrn = false(n,1);
idxTrn(randsample(n,round(0.5*n))) = true; % Training set logical indices 
idxVal = idxTrn == false;                  % Validation set logical indices

学習セットを使用して分類木を成長させます。

Mdl = fitctree(meas(idxTrn,:),species(idxTrn));

分類木を表示します。

view(Mdl,'Mode','graph');

この分類木には 4 つの枝刈りレベルがあります。レベル 0 は、(表示のように) 枝刈りされていない完全な木です。レベル 3 はルート ノードのみ (分割なし) です。

最上位レベルを除く各部分木 (枝刈りレベル) について、学習標本の分類誤差を確認します。

m = max(Mdl.PruneList) - 1;
trnLoss = resubLoss(Mdl,'Subtrees',0:m)

trnLoss = 3×1

    0.0267
    0.0533
    0.3067

• 枝刈りされていない完全な木では、学習観測値の約 2.7% が誤分類されています。

• レベル 1 まで枝刈りされた木では、学習観測値の約 5.3% が誤分類されています。

• レベル 2 (切り株) まで枝刈りされた木では、学習観測値の約 30.6% が誤分類されています。

最上位を除く各レベルで検証標本の分類誤差を確認します。

valLoss = loss(Mdl,meas(idxVal,:),species(idxVal),'Subtrees',0:m)

valLoss = 3×1

    0.0369
    0.0237
    0.3067

• 枝刈りされていない完全な木では、検証観測値の約 3.7% が誤分類されています。

• レベル 1 まで枝刈りされた木では、検証観測値の約 2.4% が誤分類されています。

• レベル 2 (切り株) まで枝刈りされた木では、検証観測値の約 30.7% が誤分類されています。

モデルの複雑さと標本外性能のバランスをとるには、Mdl をレベル 1 まで枝刈りすることを検討します。

pruneMdl = prune(Mdl,'Level',1);
view(pruneMdl,'Mode','graph')

入力引数

tree — 分類木モデル

ClassificationTree モデル オブジェクト

分類木モデル。fitctree で学習させた ClassificationTree モデル オブジェクトとして指定します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: L = resubLoss(tree,Subtrees="all") は、tree の再代入分類損失を計算するときにすべての部分木を使用するように指定します。

LossFun — 損失関数

"mincost" (既定値) | "binodeviance" | "classifcost" | "classiferror" | "exponential" | "hinge" | "logit" | "quadratic" | 関数ハンドル

損失関数。組み込みの損失関数名または関数ハンドルを指定します。

次の表に、組み込みの損失関数の値を示します。

値	説明
"binodeviance"	二項分布からの逸脱度
"classifcost"	観測誤分類コスト
"classiferror"	10 進数の誤分類率
"exponential"	指数損失
"hinge"	ヒンジ損失
"logit"	ロジスティック損失
"mincost"	最小予測誤分類コスト (事後確率である分類スコアの場合)
"quadratic"	二次損失

"mincost" は、事後確率である分類スコアに適しています。既定の設定では、分類木は分類スコアとして事後確率を返します (predict を参照)。

関数ハンドル表記を使用して独自の関数を指定します。n は X 内の観測値の個数、K は異なるクラスの個数 (numel(tree.ClassNames)) であるとします。使用する関数のシグネチャは次のようになっていなければなりません。

lossvalue = lossfun(C,S,W,Cost)

ここで

• 出力引数 lossvalue はスカラーです。

• 関数名 (lossfun) を指定します。

• C は n 行 K 列の logical 行列であり、対応する観測値が属するクラスを各行が示します。列の順序は tree.ClassNames のクラスの順序に対応します。

  各行について観測値 p がクラス q に属する場合は C(p,q) = 1 を設定することにより、C を作成します。行 p の他のすべての要素を 0 に設定します。

• S は、分類スコアの n 行 K 列の行列です。列の順序は tree.ClassNames のクラスの順序に対応します。S は分類スコアの行列で、predict の出力と同様です。

• W は、観測値の重みの n 行 1 列の数値ベクトルです。W を渡す場合、重みは合計が 1 になるように正規化されます。

• Cost は、誤分類コストの、K 行 K 列の数値行列です。たとえば、Cost = ones(K) - eye(K) は、正しい分類のコストとして 0 を、誤分類のコストとして 1 を指定します。

損失関数の詳細については、分類損失を参照してください。

例: LossFun="binodeviance"

例: LossFun=@lossfun

データ型: char | string | function_handle

Subtrees — 枝刈りレベル

0 (既定値) | 非負の整数のベクトル | "all"

枝刈りレベル。昇順の非負の整数のベクトルまたは "all" として指定します。

ベクトルを指定する場合、すべての要素が 0 から max(tree.PruneList) の範囲になければなりません。0 は枝刈りしない完全な木を、max(tree.PruneList) は完全に枝刈りした木 (つまり、ルート ノードのみ) を表します。

"all" を指定した場合、resubLoss はすべての部分木 (つまり、枝刈り順序全体) に作用します。これは、0:max(tree.PruneList) を指定することと同じです。

resubLoss では、Subtrees で指定された各レベルまで tree の枝刈りを行ってから、対応する出力引数を推定します。Subtrees のサイズにより、一部の出力引数のサイズが決まります。

関数で Subtrees を呼び出すために、tree の PruneList プロパティと PruneAlpha プロパティは空以外でなければなりません。言い換えると、fitctree を使用するときに Prune="on" を設定して tree を成長させるか、prune を使用して tree を枝刈りすることで成長させます。

例: Subtrees="all"

データ型: single | double | char | string

TreeSize — 木のサイズ

"se" (既定値) | "min"

木のサイズ。次の値のいずれかとして指定します。

• "se" — resubLoss は、損失が最小値 (L+se、ここで L と se は Subtrees における最小値) の 1 標準偏差以内である最も高い枝刈りレベルを最適な枝刈りレベル (BestLevel) として返します。

• "min" — resubLoss は、損失が最も小さい Subtrees の要素を最適な枝刈りレベルとして返します。通常、この要素は Subtrees の最小要素です。

例: TreeSize="min"

データ型: char | string

出力引数

L — 分類損失

数値ベクトル

分類損失。Subtrees と同じ長さのスカラー値のベクトルとして返されます。誤差の意味は損失関数 (LossFun) によって異なります。

SE — 損失の標準誤差

数値ベクトル

損失の標準誤差。Subtrees と同じ長さの数値ベクトルとして返されます。

Nleaf — 葉ノードの数

整数値のベクトル

枝刈りされた部分木における葉ノードの数。Subtrees と同じ長さの整数値のベクトルとして返されます。葉ノードは終端ノードであり、分割ではなく応答を与えます。

BestLevel — 最適な枝刈りレベル

数値スカラー

最適な枝刈りレベル。数値スカラーとして返されます。値は TreeSize に応じて次のようになります。

• TreeSize が "se" の場合、関数 loss は、損失が最小値 (L+se、ここで L と se は Subtrees における最小値) の 1 標準偏差以内である最も高い枝刈りレベルを返します。

• TreeSize が "min" の場合、関数 loss は、損失が最も小さい Subtrees の要素を返します。通常、これは Subtrees の最小要素です。

詳細

分類損失

"分類損失" 関数は分類モデルの予測誤差を評価します。複数のモデルで同じタイプの損失を比較した場合、損失が低い方が予測モデルとして優れていることになります。

以下のシナリオを考えます。

• L は加重平均分類損失です。

• n は標本サイズです。

• バイナリ分類は以下です。

  • y_j は観測されたクラス ラベルです。陰性クラスを示す -1 または陽性クラスを示す 1 (あるいは、ClassNames プロパティの最初のクラスを示す -1 または 2 番目のクラスを示す 1) を使用して符号化されます。

  • f(X_j) は予測子データ X の観測値 (行) j に対する陽性クラスの分類スコアです。

  • m_j = y_jf(X_j) は、y_j に対応するクラスに観測値 j を分類する分類スコアです。正の値の m_j は正しい分類を示しており、平均損失に対する寄与は大きくありません。負の値の m_j は正しくない分類を示しており、平均損失に大きく寄与します。

• マルチクラス分類 (つまり、K ≥ 3) をサポートするアルゴリズムの場合、次のようになります。

  • y_j^* は、K - 1 個の 0 と、観測された真のクラス y_j に対応する位置の 1 から構成されるベクトルです。たとえば、2 番目の観測値の真のクラスが 3 番目のクラスであり K = 4 の場合、y₂^* = [0 0 1 0]′ になります。クラスの順序は入力モデルの ClassNames プロパティ内の順序に対応します。

  • f(X_j) は予測子データ X の観測値 j に対するクラス スコアのベクトルで、長さは K です。スコアの順序は入力モデルの ClassNames プロパティ内のクラスの順序に対応します。

  • m_j = y_j^*′f(X_j).したがって m_j は、観測された真のクラスについてモデルが予測するスカラー分類スコアです。

• 観測値 j の重みは w_j です。観測値の重みは、その合計が Prior プロパティに格納された対応するクラスの事前確率になるように正規化されます。そのため、次のようになります。

  $${\displaystyle \sum _{j=1}^n{w}_j}=1.$$

この状況では、名前と値の引数 LossFun を使用して指定できる、サポートされる損失関数は次の表のようになります。

損失関数	LossFun の値	式
二項分布からの逸脱度	"binodeviance"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left\{1+\exp \left[-2m_j\right]\right\}}.$$
観測誤分類コスト	"classifcost"	$$L={\displaystyle \sum _{j=1}^n{w}_j}{c}_{y_j{\widehat{y}}_j},$$ ここで、$${\widehat{y}}_j$$ はスコアが最大のクラスに対応するクラス ラベル、$$c_{y_j{\widehat{y}}_j}$$ は真のクラスが yj である場合に観測値をクラス $${\widehat{y}}_j$$ に分類するユーザー指定のコストです。
10 進数の誤分類率	"classiferror"	$$L={\displaystyle \sum _{j=1}^n{w}_j}I\left\{{\widehat{y}}_j\ne y_j\right\},$$ ここで、I{·} はインジケーター関数です。
クロスエントロピー損失	"crossentropy"	"crossentropy" はニューラル ネットワーク モデルのみに適しています。 加重クロスエントロピー損失は次となります。 $$L=-{\displaystyle \sum _{j=1}^n\frac{{\tilde{w}}_j\log (m_j)}{Kn}},$$ ここで重み $${\tilde{w}}_j$$ は、合計が 1 ではなく n になるように正規化されます。
指数損失	"exponential"	$$L={\displaystyle \sum _{j=1}^n{w}_j\exp \left(-m_j\right)}.$$
ヒンジ損失	"hinge"	$$L={\displaystyle \sum }_{j=1}^n{w}_j\max \left\{0,1-m_j\right\}.$$
ロジスティック損失	"logit"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left(1+\exp \left(-m_j\right)\right)}.$$
最小予測誤分類コスト	"mincost"	"mincost" は、分類スコアが事後確率の場合にのみ適しています。 重み付きの最小予測分類コストは、次の手順を観測値 j = 1、...、n について使用することにより計算されます。 観測値 Xj をクラス k に分類する予測誤分類コストを推定します。 $${\gamma }_{jk}={\left(f{\left(X_j\right)}^{\prime }C\right)}_k.$$ f(Xj) は観測値 Xj のクラス事後確率の列ベクトルです。C はモデルの Cost プロパティに格納されるコスト行列です。 最小予測誤分類コストに対応するクラス ラベルを観測値 j について予測します。 $${\widehat{y}}_j=\underset{k=1,\mathrm{...},K}{\text{argmin}}{\gamma }_{jk}.$$ C を使用して、予測を行うために必要なコスト (cj) を求めます。 最小予測誤分類コスト損失の加重平均は次となります。 $$L={\displaystyle \sum _{j=1}^n{w}_j{c}_j}.$$
二次損失	"quadratic"	$$L={\displaystyle \sum _{j=1}^n{w}_j{\left(1-m_j\right)}^2}.$$

既定のコスト行列 (正しい分類の場合の要素値は 0、誤った分類の場合の要素値は 1) を使用する場合、"classifcost"、"classiferror"、および "mincost" の損失の値は同じです。既定以外のコスト行列をもつモデルでは、ほとんどの場合は "classifcost" の損失と "mincost" の損失が等価になります。これらの損失が異なる値になる可能性があるのは、最大の事後確率をもつクラスへの予測と最小の予測コストをもつクラスへの予測が異なる場合です。"mincost" は分類スコアが事後確率の場合にしか適さないことに注意してください。

次の図では、1 つの観測値のスコア m に対する損失関数 ("classifcost"、"crossentropy"、および "mincost" を除く) を比較しています。いくつかの関数は、点 (0,1) を通過するように正規化されています。

真の誤分類コスト

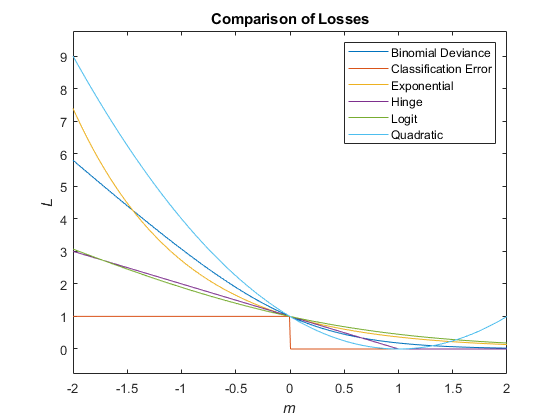
真の誤分類コストは、観測値を誤ったクラスに分類するコストです。

分類器の作成時に、名前と値の引数 Cost を使用してクラスごとの真の誤分類コストを設定できます。Cost(i,j) は、真のクラスが i の場合に観測値をクラス j に分類するコストです。既定では、Cost(i,j)=1 (i~=j の場合) および Cost(i,j)=0 (i=j の場合) です。つまり、正しい分類のコストは 0、誤った分類のコストは 1 です。

予測誤分類コスト

観測値ごとの予測誤分類コストは、観測をそれぞれのクラスに分類する平均コストです。

学習済みの分類器を使用して Nobs 個の観測値を分類するとします。また、K 個のクラスがあるとします。1 行に 1 観測ずつ、観測値を行列 X に置きます。

予測コスト行列 CE のサイズは、Nobs 行 K列です。CE の各行には、観測をそれぞれのクラス K に分類する予測 (平均) コストが含まれます。CE(n,k) は次のとおりです。

$${\displaystyle \sum _{i=1}^K\widehat{P}\left(i|X(n)\right)C\left(k|i\right)},$$

ここで

• K は、クラスの数です。

• $$\widehat{P}\left(i|X(n)\right)$$ は、観測値 X(n) のクラス i の事後確率です。

• $$C\left(k|i\right)$$ は、真のクラスが i である観測値を k に分類する真の誤分類コストです。

拡張機能

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2011a で導入

参考

loss | resubEdge | resubMargin | resubPredict | fitctree | ClassificationTree