ニューラル ネットワーク分類器の性能評価

fitcnet を使用して全結合層をもつフィードフォワード ニューラル ネットワーク分類器を作成します。モデルの過適合を防止するために、検証データを使用して学習プロセスを早期に停止します。その後、分類器のオブジェクト関数を使用してテスト データでモデルの性能を評価します。

標本データの読み込みと前処理

この例では census1994.mat に保存されている 1994 年の国勢調査データを使用します。このデータ セットは、個人の年収が $50,000 を超えるかどうかを予測するために使用できる、米国国勢調査局の人口統計情報から構成されています。

学習データ adultdata およびテスト データ adulttest を含む、標本データ census1994 を読み込みます。学習データセットの最初の数行をプレビューします。

load census1994
head(adultdata)

    age       workClass          fnlwgt      education    education_num       marital_status           occupation        relationship     race      sex      capital_gain    capital_loss    hours_per_week    native_country    salary
    ___    ________________    __________    _________    _____________    _____________________    _________________    _____________    _____    ______    ____________    ____________    ______________    ______________    ______

    39     State-gov                77516    Bachelors         13          Never-married            Adm-clerical         Not-in-family    White    Male          2174             0                40          United-States     <=50K 
    50     Self-emp-not-inc         83311    Bachelors         13          Married-civ-spouse       Exec-managerial      Husband          White    Male             0             0                13          United-States     <=50K 
    38     Private             2.1565e+05    HS-grad            9          Divorced                 Handlers-cleaners    Not-in-family    White    Male             0             0                40          United-States     <=50K 
    53     Private             2.3472e+05    11th               7          Married-civ-spouse       Handlers-cleaners    Husband          Black    Male             0             0                40          United-States     <=50K 
    28     Private             3.3841e+05    Bachelors         13          Married-civ-spouse       Prof-specialty       Wife             Black    Female           0             0                40          Cuba              <=50K 
    37     Private             2.8458e+05    Masters           14          Married-civ-spouse       Exec-managerial      Wife             White    Female           0             0                40          United-States     <=50K 
    49     Private             1.6019e+05    9th                5          Married-spouse-absent    Other-service        Not-in-family    Black    Female           0             0                16          Jamaica           <=50K 
    52     Self-emp-not-inc    2.0964e+05    HS-grad            9          Married-civ-spouse       Exec-managerial      Husband          White    Male             0             0                45          United-States     >50K  

各行には、成人 1 人の人口統計情報が格納されています。最後の列 salary は個人の年収が $50,000 以下か $50,000 を超えるかを示します。

欠損値がある adultdata と adulttest の行を table から削除します。

adultdata = rmmissing(adultdata);
adulttest = rmmissing(adulttest);

学習データとテスト データの両方で education_num と education の変数を組み合わせて、履修が修了している最も高い教育レベルを示す単一の順序付けされたカテゴリカル変数を作成します。

edOrder = unique(adultdata.education_num,"stable");
edCats = unique(adultdata.education,"stable");
[~,edIdx] = sort(edOrder);

adultdata.education = categorical(adultdata.education, ...
    edCats(edIdx),"Ordinal",true);
adultdata.education_num = [];

adulttest.education = categorical(adulttest.education, ...
    edCats(edIdx),"Ordinal",true);
adulttest.education_num = [];

学習データの分割

層化ホールドアウト分割を使用して学習データをさらに分割します。モデルの学習プロセスを早期に停止するために別の検証データ セットを作成します。観測値の約 30% を検証データ セット用に予約し、残りの観測値をニューラル ネットワーク分類器の学習に使用します。

rng("default") % For reproducibility of the partition
c = cvpartition(adultdata.salary,"Holdout",0.30);
trainingIndices = training(c);
validationIndices = test(c);
tblTrain = adultdata(trainingIndices,:);
tblValidation = adultdata(validationIndices,:);

ニューラル ネットワークの学習

学習セットを使用してニューラル ネットワーク分類器に学習させます。tblTrain の列 salary を応答、列 fnlwgt を観測値の重みとして指定し、数値予測子を標準化します。検証セットを使用して各反復でモデルを評価します。名前と値の引数 Verbose を使用して、各反復で学習データを表示するように指定します。既定では、検証クロスエントロピー損失が 6 回連続でそれまでに計算された検証クロスエントロピー損失の最小値以上になると、その時点で学習プロセスが早期に終了します。検証損失が最小値以上になる許容回数を変更するには、名前と値の引数 ValidationPatience を指定します。

Mdl = fitcnet(tblTrain,"salary","Weights","fnlwgt", ...
    "Standardize",true,"ValidationData",tblValidation, ...
    "Verbose",1);

|==========================================================================================|
| Iteration  | Train Loss | Gradient   | Step       | Iteration  | Validation | Validation |
|            |            |            |            | Time (sec) | Loss       | Checks     |
|==========================================================================================|
|           1|    0.326435|    0.105391|    1.174862|    0.043657|    0.325292|           0|
|           2|    0.275413|    0.024249|    0.259219|    0.055635|    0.275310|           0|
|           3|    0.258430|    0.027390|    0.173985|    0.069614|    0.258820|           0|
|           4|    0.218429|    0.024172|    0.617121|    0.115366|    0.220265|           0|
|           5|    0.194545|    0.022570|    0.717853|    0.063591|    0.197881|           0|
|           6|    0.187702|    0.030800|    0.706053|    0.039018|    0.192706|           0|
|           7|    0.182328|    0.016970|    0.175624|    0.037140|    0.187243|           0|
|           8|    0.180458|    0.007389|    0.241016|    0.042889|    0.184689|           0|
|           9|    0.179364|    0.007194|    0.112335|    0.029110|    0.183928|           0|
|          10|    0.175531|    0.008233|    0.271539|    0.019863|    0.180789|           0|
|==========================================================================================|
| Iteration  | Train Loss | Gradient   | Step       | Iteration  | Validation | Validation |
|            |            |            |            | Time (sec) | Loss       | Checks     |
|==========================================================================================|
|          11|    0.167236|    0.014633|    0.941927|    0.043627|    0.172918|           0|
|          12|    0.164107|    0.007069|    0.186935|    0.020543|    0.169584|           0|
|          13|    0.162421|    0.005973|    0.226712|    0.022389|    0.167040|           0|
|          14|    0.161055|    0.004590|    0.142162|    0.020381|    0.165982|           0|
|          15|    0.159318|    0.007807|    0.438498|    0.020655|    0.164524|           0|
|          16|    0.158856|    0.003321|    0.054253|    0.030839|    0.164177|           0|
|          17|    0.158481|    0.004336|    0.125983|    0.037408|    0.163746|           0|
|          18|    0.158042|    0.004697|    0.160583|    0.038954|    0.163042|           0|
|          19|    0.157412|    0.007637|    0.304204|    0.054144|    0.162194|           0|
|          20|    0.156931|    0.003145|    0.182916|    0.085170|    0.161804|           0|
|==========================================================================================|
| Iteration  | Train Loss | Gradient   | Step       | Iteration  | Validation | Validation |
|            |            |            |            | Time (sec) | Loss       | Checks     |
|==========================================================================================|
|          21|    0.156666|    0.003791|    0.089101|    0.028820|    0.161714|           0|
|          22|    0.156457|    0.003157|    0.039609|    0.034513|    0.161592|           0|
|          23|    0.156210|    0.002608|    0.081463|    0.037228|    0.161511|           0|
|          24|    0.155981|    0.003497|    0.088109|    0.029686|    0.161557|           1|
|          25|    0.155520|    0.004131|    0.181666|    0.038433|    0.161433|           0|
|          26|    0.154899|    0.002309|    0.327281|    0.038669|    0.161065|           0|
|          27|    0.154703|    0.001210|    0.055537|    0.030134|    0.160733|           0|
|          28|    0.154503|    0.002407|    0.089433|    0.029874|    0.160449|           0|
|          29|    0.154304|    0.003212|    0.118986|    0.039419|    0.160163|           0|
|          30|    0.154026|    0.002823|    0.183600|    0.032147|    0.159885|           0|
|==========================================================================================|
| Iteration  | Train Loss | Gradient   | Step       | Iteration  | Validation | Validation |
|            |            |            |            | Time (sec) | Loss       | Checks     |
|==========================================================================================|
|          31|    0.153738|    0.004477|    0.405824|    0.040489|    0.159378|           0|
|          32|    0.153538|    0.003659|    0.065795|    0.037337|    0.159333|           0|
|          33|    0.153491|    0.001184|    0.017043|    0.028284|    0.159377|           1|
|          34|    0.153460|    0.000988|    0.017456|    0.027601|    0.159446|           2|
|          35|    0.153420|    0.002433|    0.032119|    0.025374|    0.159463|           3|
|          36|    0.153329|    0.003517|    0.058506|    0.032602|    0.159478|           4|
|          37|    0.153181|    0.002436|    0.116169|    0.026235|    0.159453|           5|
|          38|    0.153025|    0.001577|    0.177446|    0.031192|    0.159377|           6|
|==========================================================================================|

オブジェクト Mdl の TrainingHistory プロパティ内の情報を使用して、検証クロスエントロピー損失が最小になる対応する反復を確認します。最終的に返されるモデル Mdl は、この反復で学習させたモデルになります。

iteration = Mdl.TrainingHistory.Iteration;
valLosses = Mdl.TrainingHistory.ValidationLoss;
[~,minIdx] = min(valLosses);
iteration(minIdx)

ans = 32

テスト セットのパフォーマンスの評価

オブジェクト関数 predict、loss、margin、および edge を使用して、学習させた分類器 Mdl の性能をテスト セット adulttest で評価します。

テスト セットの観測値の予測されるラベルと分類スコアを求めます。

[labels,Scores] = predict(Mdl,adulttest);

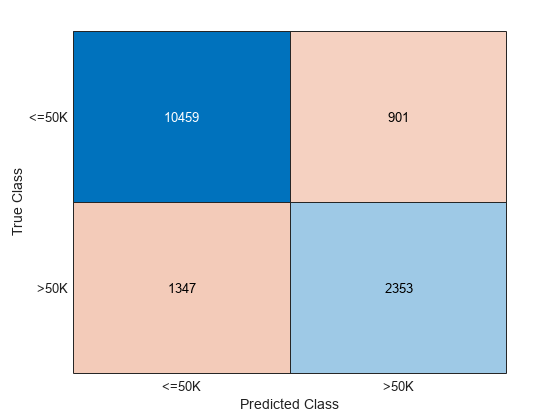
テスト セットの結果から、混同行列を作成します。対角要素は、特定のクラスの正しく分類されたインスタンスの数を示しています。非対角要素は誤分類した観測値のインスタンスです。

confusionchart(adulttest.salary,labels)

テスト セットの分類精度を計算します。

error = loss(Mdl,adulttest,"salary");
accuracy = (1-error)*100

accuracy = 85.0172

テスト セットの観測値の約 85% がニューラル ネットワーク分類器で正しく分類されています。

学習させたニューラル ネットワークのテスト セットの分類マージンを計算します。マージンのヒストグラムを表示します。

分類マージンは、真のクラスの分類スコアと偽のクラスの分類スコアの差を表します。ニューラル ネットワーク分類器から返されるスコアは事後確率であるため、分類マージンが 1 に近いほど信頼度が高い分類であることを示し、負のマージンの値は誤分類を示します。

m = margin(Mdl,adulttest,"salary");
histogram(m)

分類エッジ (分類マージンの平均) を使用して分類器の全体の性能を評価します。

meanMargin = edge(Mdl,adulttest,"salary")

meanMargin = 0.5943

あるいは、観測値の重みを使用して重み付きの分類エッジを計算します。

weightedMeanMargin = edge(Mdl,adulttest,"salary", ...
    "Weight","fnlwgt")

weightedMeanMargin = 0.6045

各点が観測値に対応する散布図を使用して、予測されるラベルと分類スコアを可視化します。予測されるラベルをもとに点の色を設定し、最大スコアをもとに点の透明度を設定します。透明度が低い点には、高い信頼度のラベルを付けます。

まず、テスト セットの各観測値の最大分類スコアを求めます。

maxScores = max(Scores,[],2);

1 週間の勤務時間と教育レベルで最大スコアを比較する散布図を作成します。教育の変数はカテゴリカルであるため、点が重ならないように y 次元に沿ってランダムに微変動させます。

カラーマップを変更して、$50,000 以下の年収に対応する最大スコアを青で表示し、$50,000 を超える年収に対応する最大スコアを赤で表示します。

scatter(adulttest.hours_per_week,adulttest.education,[],labels, ...
    "filled","MarkerFaceAlpha","flat","AlphaData",maxScores, ...
    "YJitter","rand");
xlabel("Number of Work Hours Per Week")
ylabel("Education")

Mdl.ClassNames

ans = 2x1 categorical
     <=50K 
     >50K 

colors = lines(2)

colors = 2×3

         0    0.4470    0.7410
    0.8500    0.3250    0.0980

colormap(colors);

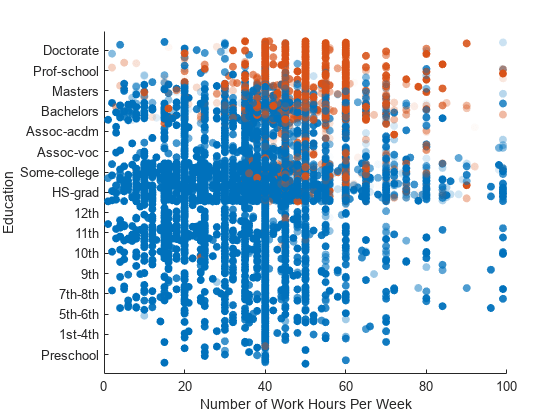
散布図の色から、ニューラル ネットワークの予測では、全般に教育レベルが低い人 (高校卒業まで) は年収が $50,000 以下となっていることがわかります。このモデルでは図の右下にある点の一部が透明になっており、1 週間の勤務時間が長い人 (60 時間以上) については予測の信頼度が低いことを示しています。

参考

fitcnet | margin | edge | loss | predict | ClassificationNeuralNetwork | confusionchart | scatter

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい