コマンド ラインを使用した線形化の結果のトラブルシューティング
この例では、コマンド ラインで LinearizationAdvisor オブジェクトを使用して Simulink® モデルの線形化をデバッグする方法を説明します。線形化の結果を対話的にトラブルシューティングすることもできます。詳細については、モデル線形化器での線形化結果のトラブルシューティングを参照してください。
モデルを開きます。
mdl = 'scdpendulum';
open_system(mdl)

振子角度の初期条件は、垂直の不安定な平衡状態である 0 度から反時計回りに 90 度です。振子角速度の初期条件は 0 deg/s です。この状態を維持するための定格トルクは -49.05 N m です。この構成はモデルの初期条件として保存されています。
モデルの線形化
モデル内で定義されている線形解析ポイントとモデルの操作点を使用してモデルを線形化します。
io = getlinio(mdl); linsys = linearize(mdl,io);
線形化の結果をチェックするため、そのボード応答をプロットします。
bode(linsys)

モデルはゼロに線形化されており、トルク tau は角度や角速度に影響を与えません。ゼロ線形化のソースを見つけるには、LinearizationAdvisorオブジェクトを使用できます。
アドバイザーを有効にした状態でのモデルの線形化
線形化中に診断情報を収集してトラブルシューティングのためのアドバイザーを作成するには、まず linearizeOptions オプション セットを作成して StoreAdvisor オプションを true に指定します。
opt = linearizeOptions('StoreAdvisor',true);
このオプション セットを使用して Simulink モデルを線形化します。線形化の診断情報を含む info 出力引数を LinearizationAdvisor オブジェクトに返します。
[linsys1,~,info] = linearize(mdl,io,opt);
LinearizationAdvisor オブジェクトを抽出します。
advisor = info.Advisor;
線形化パスの強調表示
現在の線形化の線形化パスを表示するには、highlightを使用します。
highlight(advisor)

振子サブシステムを表示します。

[線形化パス] ダイアログ ボックスに示されるように、ブロックは次のように強調表示されます。
青はモデルの線形化に数値的な影響を与えます。
赤は線形化パス上にありますが、現在の操作点とブロック パラメーターではモデルの線形化に影響しません。
モデルがゼロに線形化されるため、線形化に寄与するブロックはありません。
問題が生じる可能性のあるブロックの調査
線形化で問題が生じる可能性のあるブロックの診断情報を取得するには、adviseを使用します。この関数は、次の条件を少なくとも 1 つ満たす、線形化パス上のブロックに関する情報を含んだ新しい LinearizationAdvisor オブジェクトを返します。
自らの線形化に関する診断メッセージをもつ
ゼロに線形化する
代替の線形化をもつ
adv1 = advise(advisor);
これらのブロックの診断情報の概要を表示するには、getBlockInfoを使用します。
getBlockInfo(adv1)
ans = Linearization Diagnostics for the Blocks: Block Info: ----------- Index BlockPath Is On Path Contributes To Linearization Linearization Method 1. scdpendulum/pendulum/Saturation Yes No Exact 2. scdpendulum/angle_wrap/Trigonometric Function1 Yes No Perturbation 3. scdpendulum/pendulum/Trigonometric Function Yes No Perturbation
この場合、アドバイザーは問題が生じる可能性のある 3 つのブロック (1 つの Saturation ブロックと 2 つの Trigonometric Function ブロック) を報告します。MATLAB® でこの例を実行すると、ブロック パスがハイパーリンクとして表示されます。モデル内でこのいずれかのブロックに移動するには、対応するブロック パスのハイパーリンクをクリックします。
特定のブロック線形化についてさらに詳しい情報を表示するには、getBlockInfo を使用します。利用可能な診断の詳細については、BlockDiagnosticを参照してください。
たとえば、Saturation ブロックの診断情報を取得します。
diagInfo = getBlockInfo(adv1,1)
diagInfo =
Linearization Diagnostics for scdpendulum/pendulum/Saturation with properties:
IsOnPath: 'Yes'
ContributesToLinearization: 'No'
LinearizationMethod: 'Exact'
Linearization: [1×1 ss]
OperatingPoint: [1×1 linearize.advisor.BlockOperatingPoint]
このブロックには、ブロックの線形化の結果に関する次の 2 つの診断メッセージがあります。
信号入力値 (-49.05) がブロックの下限 (-49) を外れているため、ブロックは解析的に 0 に線形化されます。ブロックをゲインとして線形化することを検討してください。
ブロックの線形化に少なくとも 1 つのゼロの入力/出力のペアがあり、その結果、システムの線形化でゼロの入力/出力のペアが 1 つ生じています。モデルの線形化に対するブロックの寄与が想定されている場合は、ブロック パラメーターまたは操作点、あるいはその両方を変更してください。
最初のメッセージは、入力操作点が -49.05 なので、ブロックがその飽和の下限 -49 の外で線形化されていることを示します。
メッセージにはまた、ブロックをゲインとして線形化でき、その場合はブロックが入力操作点には無関係に 1 として線形化されることも示されています。
MATLAB でこの例を実行すると、[ブロックをゲインとして線形化] というテキストがハイパーリンクとして表示されます。Saturation ブロックの [ブロック パラメーター] ダイアログ ボックスを開き、ブロックをゲインとして線形化するためのオプションを強調表示するには、このハイパーリンクをクリックします。

[線形化時にゲインとして扱う] を選択し、[OK] をクリックします。
あるいは、コマンド ラインからこのパラメーターを設定することもできます。
set_param('scdpendulum/pendulum/Saturation','LinearizeAsGain','on')
2 番目の診断メッセージは、このブロックの線形化によってモデル全体がゼロに線形化することを示しています。このブロックの線形化を表示します。
diagInfo.Linearization
ans =
D =
u1
y1 0
Name: Saturation
Static gain with offsets.
このブロックはゼロに線形化されるため、ブロックをゲインとして扱いブロック線形化を変更することは、非ゼロのモデル線形化を得るための最初のステップとして良い方法です。
モデルの再線形化
Saturation ブロックをゲインとして扱うことの効果を確認するには、モデルを再線形化してそのボード線図をプロットします。
[linsys2,~,info] = linearize(mdl,io,opt); bode(linsys2)
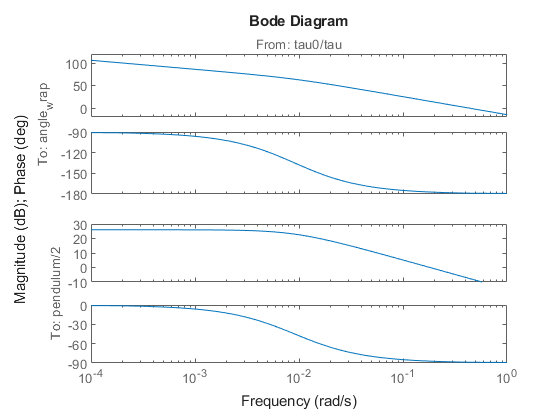
モデルの線形化は非ゼロになりました。
いずれかのブロックでまだ線形化に問題が生じる可能性があるかどうかをチェックするには、アドバイザー オブジェクトを抽出し、関数 advise を使用します。
advisor2 = info.Advisor; adv2 = advise(advisor2);
ブロックの診断情報を表示します。
getBlockInfo(adv2)
ans = Linearization Diagnostics for the Blocks: Block Info: ----------- Index BlockPath Is On Path Contributes To Linearization Linearization Method 1. scdpendulum/angle_wrap/Trigonometric Function1 Yes No Perturbation 2. scdpendulum/pendulum/Trigonometric Function Yes No Perturbation
2 つの Trigonometric Function ブロックは引き続き表示されています。
更新された線形化の線形化パスを強調表示します。
highlight(advisor2)
振子サブシステムを表示します。

これらのブロックが線形化に寄与しない理由を理解するには、対応するブロック診断情報を確認します。たとえば、2 番目の Trigonometric Function ブロックに関する診断情報を取得します。
diagInfo = getBlockInfo(adv2,2)
diagInfo =
Linearization Diagnostics for scdpendulum/pendulum/Trigonometric Function with properties:
IsOnPath: 'Yes'
ContributesToLinearization: 'No'
LinearizationMethod: 'Perturbation'
Linearization: [1×1 ss]
OperatingPoint: [1×1 linearize.advisor.BlockOperatingPoint]
このブロックの線形化を表示します。
diagInfo.Linearization
ans =
D =
u1
y1 0
Name: Trigonometric
Function
Static gain with offsets.
ブロックはゼロに線形化します。この結果がブロックの現在の操作点で予想されるものかどうかを調べるには、その操作点をチェックします。
diagInfo.OperatingPoint
ans = Block Operating Point for scdpendulum/pendulum/Trigonometric Function Inputs: ------- Port u 1 1.5708
ブロックの入力操作点は  です。
です。
入力について関数 sin の 1 次導関数を取ることにより、ブロックの線形化を解析的に求めることができます。
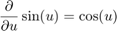
したがって、 で評価される場合のブロックの線形化はゼロになります。入力のソースは 2 次積分器の最初の出力で、これは状態
で評価される場合のブロックの線形化はゼロになります。入力のソースは 2 次積分器の最初の出力で、これは状態 theta に依存します。したがって、 の場合、このブロックはゼロに線形化します。ここで、
の場合、このブロックはゼロに線形化します。ここで、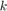 は整数です。angle_wrap サブシステムのもう一方の Trigonometric Function ブロックにも同じ条件が適用されます。これらのブロックでゼロ線形化が予想されていなければ、操作点の状態
は整数です。angle_wrap サブシステムのもう一方の Trigonometric Function ブロックにも同じ条件が適用されます。これらのブロックでゼロ線形化が予想されていなければ、操作点の状態 theta を変更して、モデルを再線形化することができます。
カスタム クエリの作成と実行
線形化アドバイザーには、カスタム クエリを作成するためのオブジェクトと関数も用意されています。これらのクエリを使用して、モデル内で特定の条件に一致するブロックを検出できます。たとえば、数値摂動法を使用して線形化されるすべての SISO ブロックを見つけるには、まず次の各検索条件用にクエリ オブジェクトを作成します。
1 つの入力をもつ
1 つの出力をもつ
数値的に摂動される
qIn = linqueryHasInputs(1); qOut = linqueryHasOutputs(1); qPerturb = linqueryIsNumericallyPerturbed;
論理演算子を使用してこれらのクエリ オブジェクトを組み合わせてCompoundQueryオブジェクトを作成します。
sisopert = qIn & qOut & qPerturb;
advisor2 のブロック診断で、これらの条件に一致するブロックを検索します。
sisopertBlocks = find(advisor2,sisopert)
sisopertBlocks =
LinearizationAdvisor with properties:
Model: 'scdpendulum'
OperatingPoint: [1×1 opcond.OperatingPoint]
BlockDiagnostics: [3×1 linearize.advisor.BlockDiagnostic]
QueryType: '((Has 1 Inputs & Has 1 Outputs) & Perturbation)'
モデルには数値摂動法を用いて線形化される SISO ブロックが 3 つあります。
カスタム クエリの使用の詳細については、線形化の結果で特定の条件に一致するブロックの検出を参照してください。
bdclose(mdl)