ディーゼルエンジンの MIMO 制御

この例では、systune を使用してディーゼルエンジンの MIMO コントローラーを設計および調整します。このコントローラーは、単一の操作条件の離散時間で調整されます。

ディーゼルエンジンモデル

最新ディーゼルエンジンでは可変容量ターボ (VGT) と排気ガス再循環 (EGR) を使用して排気を削減します。厳格な排気目標を達成するには、VGT 給気圧と EGR マスフローの厳格な制御が必要です。この例では、射出シリンダーあたり 12 mg の燃料質量を使用してエンジンが 2100 rpm で動作する場合に、これらの 2 つの変数を制御する MIMO コントローラーを設計および調整する方法を説明します。

open_system('rct_diesel')

VGT/EGR 制御システムは Simulink でモデル化されます。コントローラーは、EGR バルブおよび VGT バルブの位置 EGRLIFT と VGTPOS を調整します。コントローラーは給気圧と EGR マスフローの目標値および測定値に加え、燃料質量とエンジン速度の測定値にもアクセスします。両方のバルブにレートと飽和の制限があります。プラントモデルは 0.1 秒ごとにサンプリングされ、制御信号 EGRLIFT および VGTPOS は 0.2 秒おきに更新されます。この例では、給気圧 +10 KPa および EGR マスフロー +3 g/s のステップ変化と、燃料質量 +5 mg および速度 -200 rpm の外乱を検討します。

検討対象の操作条件で、システム同定を使用して実験データからエンジンの線形モデルを導き出しました。操作変数 EGRLIFT および VGTPOS から制御変数 BOOST および EGR MF への周波数応答が次のように表示されます。プラントは低周波数で悪条件となるため、給気圧と EGR マスフローを個々に制御するのが難しくなる点に注意してください。

sigma(Plant(:,1:2)), grid
title('Frequency response of the linearized engine dynamics')

制御目的

次の 2 つの主要な制御目的があります。

給気圧および EGR マスフローのステップ変化に対して最小の相互干渉で約 5 秒間で応答する
速度および燃料質量における (小さな) 変化に影響されない

1 つ目の目的には追従要件を使用します。相互干渉がこれらの変化に対して "相対的" に小さくなるようにステップ変化の振幅を指定します。

% 5-second response time, steady-state error less than 5%
TR = TuningGoal.Tracking({'BOOST REF';'EGRMF REF'},{'BOOST';'EGRMF'},5,0.05);
TR.Name = 'Setpoint tracking';
TR.InputScaling = [10 3];

2 番目の目的では、速度と燃料質量の変化をステップ外乱として扱い、給気圧と EGR マスフローで結果として生じる変化のピーク振幅と整定時間を指定します。また、各外乱の相対的な寄与を適切に反映する信号振幅を指定します。

% Peak<0.5, settling time<5
DR = TuningGoal.StepRejection({'FUELMASS';'SPEED'},{'BOOST';'EGRMF'},0.5,5);
DR.Name = 'Disturbance rejection';
DR.InputScaling = [5 200];
DR.OutputScaling = [10 3];

モデル化していないダイナミクスとエイリアシングに十分なロバスト性を提供するには、制御帯域幅を制限し、プラントの入力と出力の両方に十分な安定余裕を適用します。扱っているのが 2 行 2 列の MIMO フィードバックループであるため、この要件は各フィードバックチャネルでのゲイン変動または位相変動の安定性を保証します。ゲインまたは位相は一度に両方のチャネルで変化する可能性があり、その変化量はチャネルごとに異なります。詳細については、制御システムの調整における安定余裕およびTuningGoal.Marginsを参照してください。

% Roll off of -20 dB/dec past 1 rad/s
RO = TuningGoal.MaxLoopGain({'EGRLIFT','VGTPOS'},1,1);
RO.LoopScaling = 'off';
RO.Name = 'Roll-off';

% 7 dB of gain margin and 45 degrees of phase margin
M1 = TuningGoal.Margins({'EGRLIFT','VGTPOS'},7,45);
M1.Name = 'Plant input';
M2 = TuningGoal.Margins('DIESEL ENGINE',7,45);
M2.Name = 'Plant output';

ブラックボックス MIMO コントローラーの調整

最適な制御構造の事前知識がない場合は、最初にさまざまな次数の "ブラックボックス" 状態空間コントローラーを試します。プラントモデルには 4 つの状態があるため、4 以下の次数のコントローラーを試します。ここでは、Simulink モデルの "SS2" ブロックに 2 つの状態があるため 2 次コントローラーを調整します。

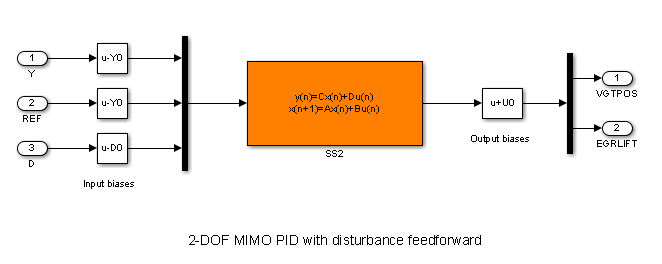
図 1: 2 次のブラックボックスコントローラー

slTuner インターフェイスを使用して Simulink モデルを調整用に構成します。ブロック "SS2" を調整可能としてマークし、余裕とループ整形を評価する位置を登録して、線形化と調整をコントローラーのサンプリングレートで実行することを指定します。

ST0 = slTuner('rct_diesel','SS2');
ST0.Ts = 0.2;
addPoint(ST0,{'EGRLIFT','VGTPOS','DIESEL ENGINE'})

ここで、systune を使用して制御目的に従って状態空間コントローラーを調整します。安定余裕とロールオフターゲットを厳密な制約として扱い、可能な限り残りの目的 (柔軟な目標) を満たすように試みます。開始点をランダム化して望ましくない局所的最小値になるリスクを削減します。

Opt = systuneOptions('RandomStart',2);
rng(0), ST1 = systune(ST0,[TR DR],[M1 M2 RO],Opt);

Final: Soft = 1.05, Hard = 0.98938, Iterations = 545
Final: Soft = 1.05, Hard = 0.97621, Iterations = 499
Final: Soft = 1.05, Hard = 0.96779, Iterations = 479

すべての要件はほぼ満たされます (正規化された値が 1 未満の場合に要件は満たされます)。これをグラフで確認します。

figure('Position',[10,10,1071,714])
viewGoal([TR DR RO M1 M2],ST1)

設定点の追従と外乱の抑制の応答をプロットします。信号振幅でスケーリングして正規化の効果を示します (給気圧は +10 KPa、EGR マスフローは +3 g/s、燃料質量は +5 mg および速度は -200 rpm ずつ変化します)。

figure('Position',[100,100,560,500])
T1 = getIOTransfer(ST1,{'BOOST REF';'EGRMF REF'},{'BOOST','EGRMF','EGRLIFT','VGTPOS'});
T1 = diag([1/10 1/3 1 1]) * T1 * diag([10 3]);
subplot(211), step(T1(1:2,:),15), title('Setpoint tracking')
subplot(212), step(T1(3:4,:),15), title('Control effort')

D1 = getIOTransfer(ST1,{'FUELMASS';'SPEED'},{'BOOST','EGRMF','EGRLIFT','VGTPOS'});
D1 = diag([1/10 1/3 1 1]) * D1 * diag([5 -200]);
subplot(211), step(D1(1:2,:),15), title('Disturbance rejection')
subplot(212), step(D1(3:4,:),15), title('Control effort')

コントローラーは、変数 BOOST と変数 EGRMF 間の最小の相互干渉により 5 秒未満で応答します。

簡略化された制御構造の調整

状態空間コントローラーはそのまま実装されますが、多くの場合、より簡略化された一般的な構造に要約することをお勧めします。これを行うには、調整後のコントローラーを取得し、その周波数応答を検証します。

C = getBlockValue(ST1,'SS2');

clf
bode(C(:,1:2),C(:,3:4),{.02 20}), grid
legend('REF to U','Y to U')

bodemag(C(:,5:6)), grid
title('Bode response from FUELMASS/SPEED to EGRLIFT/VGTPOS')

最初のプロットは、コントローラーが実質的に REF-Y (制御変数のターゲット値と実際の値の差) で動作する PI コントローラーと同様に動作することを示しています。2 番目のプロットは、測定された外乱から操作変数への伝達をラグネットワークと直列のゲインで置き換えることができることを示しています。最終的に、これは 1 次外乱フィードフォワードを使用する MIMO PI コントローラーで構成される次の簡略化された制御構造を示します。

図 2: 簡略化された制御構造

Variant Subsystem を使うと、同じ Simulink モデルに両方の制御構造を実装し、変数を使用してそれらを切り換えることができます。ここでは、MODE=2 を設定することで、MIMO PI 構造体を選択します。前と同様に、systune を使用して、簡略化された制御構造で 3 つの 2 行 2 列のゲイン行列 Kp、Ki、Kff を使用します。

% Select "MIMO PI" variant in "CONTROLLER" block
MODE = 2;

% Configure tuning interface
ST0 = slTuner('rct_diesel',{'Kp','Ki','Kff'});
ST0.Ts = 0.2;
addPoint(ST0,{'EGRLIFT','VGTPOS','DIESEL ENGINE'})

% Tune MIMO PI controller.
ST2 = systune(ST0,[TR DR],[M1 M2 RO]);

Final: Soft = 1.09, Hard = 0.99694, Iterations = 267

この場合もすべての要件がほぼ満たされます。閉ループ応答をプロットし、状態空間設計と比較します。

clf
T2 = getIOTransfer(ST2,{'BOOST REF';'EGRMF REF'},{'BOOST','EGRMF','EGRLIFT','VGTPOS'});
T2 = diag([1/10 1/3 1 1]) * T2 * diag([10 3]);
subplot(211), step(T1(1:2,:),T2(1:2,:),15), title('Setpoint tracking')
legend('SS2','PI+FF')
subplot(212), step(T1(3:4,:),T2(3:4,:),15), title('Control effort')

D2 = getIOTransfer(ST2,{'FUELMASS';'SPEED'},{'BOOST','EGRMF','EGRLIFT','VGTPOS'});
D2 = diag([1/10 1/3 1 1]) * D2 * diag([5 -200]);
subplot(211), step(D1(1:2,:),D2(1:2,:),15), title('Disturbance rejection')
legend('SS2','PI+FF')
subplot(212), step(D1(3:4,:),D2(3:4,:),15), title('Control effort')

ブラックボックス制御構造と簡略化された制御構造で同様のパフォーマンスが実現されます。PI ゲインとフィードフォワードゲインの調整後の値を検証します。

showTunable(ST2)

Block 1: rct_diesel/CONTROLLER/MIMO PID/Kp =
 
  D = 
               u1          u2
   y1   -0.007986  -0.0008203
   y2    -0.02044     0.01448
 
Name: Kp
Static gain.

-----------------------------------

Block 2: rct_diesel/CONTROLLER/MIMO PID/Ki =
 
  D = 
             u1        u2
   y1  -0.01054  -0.01416
   y2  -0.03013   0.04679
 
Name: Ki
Static gain.

-----------------------------------

Block 3: rct_diesel/CONTROLLER/MIMO PID/Kff =
 
  D = 
               u1          u2
   y1     0.01289  -9.148e-05
   y2     0.03789   -0.001472
 
Name: Kff
Static gain.