昇圧コンバーターの入力アドミタンスと出力インピーダンスを測定するための周波数応答の推定

この例では次を使用します。

この例では、Simscape™ Electrical™ コンポーネントを使用して Simulink® でモデル化された昇圧コンバーターの入力アドミタンスと出力インピーダンスを測定する方法を示します。この例では、既存のパワーエレクトロニクス回路モデルの入力アドミタンスと出力インピーダンスを測定する周波数応答推定プロセスを使用します。

一般に、パワーエレクトロニクスシステムのこれらの測定には、それらのモデルに対する大規模な変更が必要になります。ただし、Simulink Control Design™ ソフトウェアのツールを使用すれば、周波数応答の推定を実行することでパワーエレクトロニクス回路のこれらの重要な特性を測定できます。この例では、さらに、推定された周波数応答の結果を、コンポーネントのパラメーターを使用して作成された解析的伝達関数モデルと比較します。

昇圧コンバーターモデル

この例では、昇圧コンバーターモデル scdboostconverter に基づくモデルを使用します。以下について測定するために、元のモデルが次のように変更されています。

入力電流の測定用に Probe ブロックが追加されています。入力アドミタンスの周波数応答モデルを推定するために、モデルの入力電圧と入力電流に [入力の摂動] と [出力の測定] の線形解析ポイントがそれぞれ含まれています。
Controlled Current Source ブロックが負荷と並列に追加されています。出力インピーダンスの周波数応答モデルを推定するために、モデルの電流源と出力電圧に [入力の摂動] と [出力の測定] の線形解析ポイントがそれぞれ含まれています。

このモデルを調べて詳細を確認できます。

モデルを開きます。

mdl = 'scdboostconverterMeasureAdmittanceImpedance';
open_system(mdl)

サブシステムの Boost Converter ブロックバージョンを使用するには、モデルで Boost Converter ブロックをクリックするか、または次のコマンドを使用します。

set_param([mdl '/Boost Converter'],...
    'OverrideUsingVariant','block_boost_converter')

推定用の 2 値疑似乱数列と sinestream の入力信号の作成

2 値疑似乱数信号 (PRBS) は、2 つの値の間で切り替わるホワイトノイズのようなプロパティをもつ、周期的で確定的な信号です。PRBS は、最大周期の長さが $2^{n} - 1$ の本来的に周期的な信号です。ここで、 $n$ は PRBS の次数です。詳細については、PRBS 入力信号を参照してください。

次の構成で PRBS を作成します。

非周期的な PRBS を使用するには周期数を 1 に設定する。
PRBS の次数 14 を使用して、長さが 16,383 の信号を作成する。正確な周波数応答推定を取得するには、PRBS の長さは十分に大きくなければなりません。
PRBS のインジェクション周波数を 200 kHz に設定してモデルのサンプル時間に一致させる。つまり、サンプル時間を 5e-6 秒に指定します。
システムが適切に励起されるよう、摂動振幅を 1 に設定する。

in_PRBS = frest.PRBS('Order',14,'NumPeriods',1,'Amplitude',1,'Ts',5e-6);

200 rad/s から 600,000 rad/s までの 30 個の周波数をもつ sinestream 入力信号を作成します。入力信号の振幅を PRBS 入力信号に合わせて 0.5 に設定します。

in_Sinestream = frest.createFixedTsSinestream(5e-06,{200,6e5});
in_Sinestream.Amplitude = 0.5;

使用する入力信号によって、周波数応答推定プロセスのシミュレーション時間に差が生じます。同様の結果を得るためにかかるシミュレーション時間は、一般に PRBS 入力信号の方が sinestream 入力信号よりもはるかに短くなります。ここでは、in_PRBS のシミュレーション時間は in_Sinestream の約 15% になっています。

in_PRBS による周波数応答推定のシミュレーション時間を表示します。

in_PRBS.getSimulationTime

ans = 0.0819

in_Sinestream による周波数応答推定のシミュレーション時間を表示します。

in_Sinestream.getSimulationTime

ans = 0.5207

この例では、これらの入力信号を使用して、入力アドミタンス測定と出力インピーダンス測定の両方の周波数応答モデルを推定できます。

モデルの操作点の検出

昇圧コンバーターの周波数応答を推定するには、まず、コンバーターが動作する定常状態の操作点を特定しなければなりません。操作点の検出の詳細については、Simscape モデルの定常状態の操作点の検出を参照してください。この例では、0.045 秒でのシミュレーションのスナップショットから推定された操作点を使用します。

opini = findop(mdl,0.045);

計算した操作点でモデルを初期化します。

set_param(mdl,'LoadInitialState','on','InitialState','getstatestruct(opini)')

入力アドミタンスの測定

周波数応答データを収集するため、コマンドラインでプラントの周波数応答を推定できます。これを行うには、まず入力と出力の線形解析ポイントをモデルから取得します。

io_Yin(1) = linio([mdl,'/PID Controller'],1,'loopbreak');
io_Yin(2) = linio([mdl,'/Sampling'],1,'loopbreak');
io_Yin(3) = linio([mdl,'/Vin Value'],1,'input');
io_Yin(4) = linio([mdl,'/Rate Transition1'],1,'output');

モデルの初期条件を使用して操作点を指定します。

op_Yin = operpoint(mdl);

線形化出力の信号パスで時変信号を生成するすべてのソースブロックを検出します。このような時変信号は、線形化出力ポイントでの信号を妨げ、推定結果が不正確になる可能性があります。

srcblksYin = frest.findSources(mdl,io_Yin);

時変ソースブロックを無効にするには、frestimateOptions オプションセットを作成して BlocksToHoldConstant オプションを指定します。

optsYin = frestimateOptions;
optsYin.BlocksToHoldConstant = srcblksYin;

PRBS 入力信号を使用して周波数応答を推定します。

sysestYin_prbs = frestimate(mdl,io_Yin,op_Yin,in_PRBS,optsYin);

PRBS 入力信号を使用した周波数応答の推定では、多数の周波数点を含む結果が得られます。Simulink Control Design ソフトウェアでは、モデル線形化器アプリを使用してプラントの周波数応答を推定できます。モデル線形化器を使用して、コマンドラインで推定された周波数応答をさらに改善することもできます。

モデル線形化器の [結果の間引き] 機能を使用して、推定された周波数応答モデルから目的の周波数範囲と周波数点の数を指定して、内挿された結果を抽出できます。詳細については、結果の間引きを参照してください。

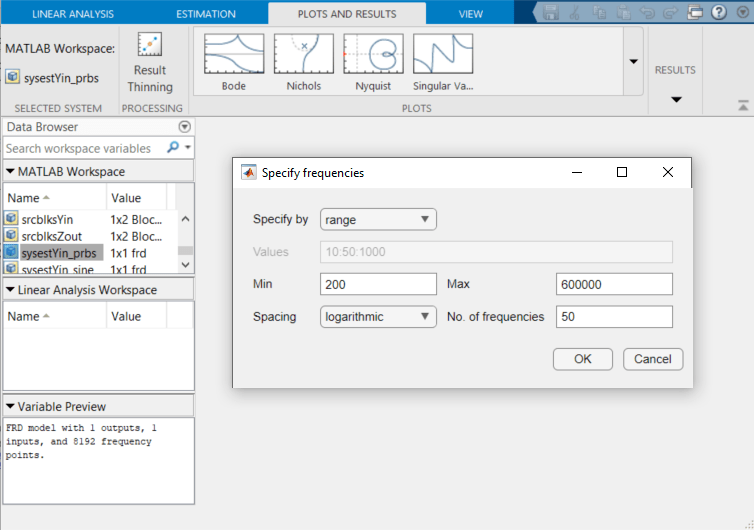
200 rad/s から 600,000 rad/s までの対数的に等間隔な 50 個の周波数点についての sysestYin_prbs に間引きを適用します。

[OK] をクリックします。間引きされたモデル sysestYin_prbs_thinned が MATLAB® ワークスペースに表示されます。あるいは、この例で用意されている間引きされた結果を使用します。

比較のために、定義済みの sinestream 入力信号を使用して周波数応答を推定します。周波数応答を推定するには、コマンドウィンドウで以下を実行します。

sysestYin_sine = frestimate(mdl,io_Yin,op_Yin,in_Sinestream,optsYin);

sinestream 信号を使用した推定には時間がかかるため、この例では、この入力信号を使用して推定されたモデルを用意してあります。

出力インピーダンスの測定

このモデルの周波数応答の推定には、この例の前の節で説明したワークフローを使用できます。線形解析ポイントの設定が少し異なります。

モデルから線形解析ポイントを取得します。

io_Zout(1) = linio([mdl,'/PID Controller'],1,'loopbreak');
io_Zout(2) = linio([mdl,'/Sampling'],1,'loopbreak');
io_Zout(3) = linio([mdl,'/Constant'],1,'input');
io_Zout(4) = linio([mdl,'/Rate Transition2'],1,'output');

モデルの初期条件を使用して操作点を指定します。

op_Zout = operpoint(mdl);

時変ソースブロックを無効にします。

srcblksZout = frest.findSources(mdl,io_Zout);
optsZout = frestimateOptions;
optsZout.BlocksToHoldConstant = srcblksZout;

PRBS 入力信号を使用して周波数応答を推定します。

sysestZout_prbs = frestimate(mdl,io_Zout,op_Zout,in_PRBS,optsZout);

"モデル線形化器" を使用して、200 rad/s から 600,000 rad/s までの対数的に等間隔な 50 個の周波数点についての sysestZout_prbs に結果の間引きを適用します。あるいは、この例で用意されている間引きされた結果を使用します。

sysestZout_sine = frestimate(mdl,io_Zout,op_Zout,in_Sinestream,optsZout);

sinestream 信号を使用した推定には時間がかかるため、この例では、この入力信号を使用して推定されたモデルを用意してあります。

解析的伝達関数

推定結果をコンポーネントのパラメーターに基づく解析的伝達関数と比較します。モデルの次のパラメーターを使用します。

L = 20e-6;
C = 1480e-6;
R = 6;
rC = 8e-3;
rL = 1.8e-3;

解析的伝達関数を計算するには、実際のデューティ比の値が必要です。この昇圧コンバーターでは、ログに記録された操作点におけるデューティ比を使用します。

D = 0.734785;
d = 1-D;

昇圧コンバーターモデルのコンポーネントのパラメーターを使用して、入力アドミタンスと出力インピーダンスの解析的伝達関数を定義します ([1] に基づきます)。

Yin = tf([C*(R+rC) 1], [L*C*(R+rC) L+C*rL*(R+rC)+C*R*rC-R*D*C*rC R+rL-R*D-R^2*D*d/(R+rC)]);
Zout = tf(R*[C*rC*L L+C*rC*(rL+R*D*rC*d/(R+rC)) rL+R*D*rC*d/(R+rC)], ...
    [L*C*(R+rC) L+C*rL*(R+rC)+C*R*rC-R*D*C*rC R+rL-R*D-R^2*D*d/(R+rC)]);

より正確に説明すると、伝達関数 Yin では PWM 信号に起因する遅延を考慮します。

N = 0.5;
Ts = 5e-6;
iodelay = N*Ts; % 0.5 PWM
Yin.IODelay = iodelay;

周波数応答データの解析的伝達関数との比較

PRBS および sinestream の入力信号を使用した周波数応答推定 (FRE) の結果を、目的の周波数範囲について解析的伝達関数と比較します。

前に保存したセッションから間引きされた PRBS の結果と sinestream の結果を読み込みます。

load sysest_prbs_thinned_yin_zout
load sysest_sine_yin_zout

入力アドミタンスの結果を比較します。

figure
bode(sysestYin_prbs_thinned,'b-')
hold on
bode(sysestYin_sine,'k*-')
bode(Yin,'r--',{10,1e6})
legend('FRE result using PRBS','FRE result using sinestream','Analytical result',...
    'Location','best')
title([{'Comparison of Estimated Frequency Responses with'},...
    {'Analytical Transfer Function for Input Admittance'}])
grid on

出力インピーダンスの結果を比較します。

figure
bode(sysestZout_prbs_thinned,'b-')
hold on
bode(sysestZout_sine,'k*-')
bode(Zout,'r--',{10,1e6})
legend('FRE result using PRBS','FRE result using sinestream','Analytical result',...
    'Location','best')
title([{'Comparison of Estimated Frequency Responses with'},...
    {'Analytical Transfer Function for Output Impedance'}])
grid on

ボード線図を調べます。PRBS 入力信号を使用して得られた FRE の結果から対象の周波数領域プロパティが取り込まれます。たとえば、振幅のピーク付近においては、PRBS 入力信号を使用した周波数応答の推定結果の方が sinestream 入力信号を使用した周波数応答の推定結果よりも解析的伝達関数と一致しています。

モデルを閉じます。

close_system(mdl,0);

参考文献

[1] Ahmadi, Reza, and Mehdi Ferdowsi. "Modeling Closed-Loop Input and Output Impedances of DC-DC Power Converters Operating inside Dc Distribution Systems." In 2014 IEEE Applied Power Electronics Conference and Exposition - APEC 2014, 1131–38, 2014. https://doi.org/10.1109/APEC.2014.6803449.

参考

frest.PRBS | frest.createFixedTsSinestream | frestimate | frestimateOptions