Simulink の可変ステップソルバー

"可変ステップソルバー" では、シミュレーション実行中にステップサイズが変化します。モデルの状態が急激に変動しているときは精度を上げるためにステップサイズが小さくなり、モデルの状態の変動が緩慢なときは不必要なステップを取ることを回避するためにステップサイズが大きくなります。ステップサイズの計算は、各ステップで計算のオーバーヘッドを加えますが、ステップの総数は減らすことが可能なため、急激に変化あるいは区分的に連続状態をもつモデルの指定したレベルの精度を保持するために必要なシミュレーション時間が増加します。

[ソルバー] コンフィギュレーションペインの [タイプ] コントロールが [Variable-step] に設定されている場合は、[ソルバー] コントロールを使用して、いずれかの可変ステップソルバーを選択できます。固定ステップソルバーと同様に、可変ステップソルバーのセットは、離散ソルバーと連続ソルバーの集合で構成されます。ただし、固定ステップソルバーとは異なり、ステップサイズは局所誤差に応じて動的に変化します。

2 つのタイプの可変ステップソルバー間の選択は、モデル内のブロックが状態を定義するかどうかと、定義する場合は、定義する状態の種類により異なります。モデルが状態を定義しない、または離散状態のみを定義する場合は、離散ソルバーを選択します。モデルが連続状態をもつ場合、連続ソルバーは、次のタイムステップで連続状態の値を計算するために数値積分を使用します。

メモ

モデルが状態をもたないまたは離散状態のみをもつ場合は、連続ソルバーを指定しても、Simulink^® は離散ソルバーを使用してモデルをシミュレートします。

可変ステップ離散ソルバー

可変ステップ離散ソルバーは、モデルが連続状態を含まないときに使用します。そのようなモデルでは、可変ステップ離散ソルバーは、ゼロクロッシングなどのモデルイベントをキャプチャするためにステップサイズを小さくし、シミュレーションの性能を向上することが可能な際にステップサイズを大きくします。

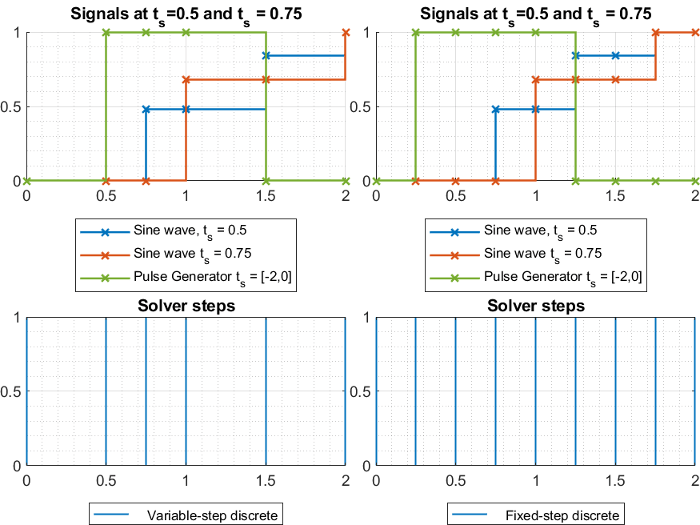
この図に示すモデルには、サンプル時間 0.5 と 0.75 に、2 つの離散正弦波が含まれます。以下のグラフは、モデル内の信号とソルバーステップを可変ステップ離散ソルバーと固定ステップ離散ソルバーのそれぞれについて示したものです。可変ステップソルバーでは、各ブロックからの出力信号を記録するために必要なステップのみが使用されていることが分かります。一方、固定ステップソルバーでは、すべての信号を記録するために固定ステップサイズ (または基本サンプル時間) の 0.25 でシミュレートする必要があるため、全体として多くのステップが使用されます。

可変ステップ連続ソルバー

可変ステップソルバーでは、シミュレーション中にステップサイズが動的に変化します。これらの各ソルバーは局所エラー制御を使用して、指定された許容誤差内に収まるようにステップサイズの増減を行います。各タイムステップでのステップサイズの計算は、計算のオーバーヘッドに加えられます。ただし、ステップの総数を減らすことができ、それによって、指定したレベルの精度を維持するために必要なシミュレーション時間を減らせます。

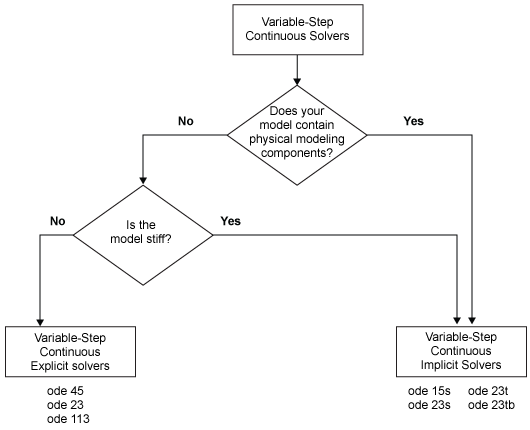
可変ステップ連続ソルバーは、1 ステップまたはマルチステップ、単一次数または可変次数、陽的または陰的などのようにさらに分けられます。詳細については、1 ステップ連続ソルバーとマルチステップ連続ソルバーを参照してください。

陽的な可変ステップ連続ソルバー

陽的な可変ステップソルバーは、スティッフでない問題用に設計されています。Simulink には次の 4 種類のソルバーが用意されています。

ode45
ode23
ode113
odeN

ODE ソルバー	1 ステップ法	マルチステップ法	精度の次数	メソッド
`ode45`	X		中	ルンゲ・クッタ、Dormand-Prince (4,5) の組
`ode23`	X		低	Bogacki と Shampine による Runge-Kutta (2,3) の組
`ode113`		X	可変、低から高	Adams-Bashforth-Moutlon の PECE 実装
`odeN`	X		陽的な固定ステップ連続ソルバーの精度の次数を参照	陽的な固定ステップ連続ソルバーの積分手法を参照

ODE ソルバー	使用時
ode45	一般に、`ode45` は、ほとんどの問題に対して最初の試みとして適用する最良のソルバーです。ルンゲ・クッタ (4,5) ソルバーは、誤差の 4 次推定を行う 5 次法です。このソルバーでも 4 次の内挿を使用して、イベント位置選定とより滑らかなプロットを実現します。 `ode45` の計算が遅い場合、問題はスティッフである可能性があるため、陰的なソルバーが必要になります。
ode113	厳密な許容誤差の問題または計算量の多い問題に対しては、Adams-Bashforth-Moulton PECE ソルバーが `ode45` よりも効率的な場合があります。
ode23	`ode23` は、粗い誤差許容量およびある程度のスティッフ性が存在するときに、`ode45` ソルバーよりも効率的な場合があります。このソルバーは、ステップの最後に計算された値と勾配に 3 次エルミート内挿を適用することで正確な解をもたらします。
odeN	`odeN` は、次数が [ソルバーの次数] パラメーターによって決定される非適応型のルンゲ・クッタ積分を使用するソルバーです。`odeN` では、[最大ステップサイズ] パラメーターによって決定される固定ステップサイズを使用しますが、ステップサイズを小さくすることでゼロクロッシングや離散サンプルヒットなどの特定のソルバーイベントを取得できます。

メモ

シミュレーション速度が重要な場合は、odeN ソルバーを選択します。たとえば、次のような場合です。

モデルにゼロクロッシングやソルバーのリセットが多数含まれている
モデルのプロファイリング時に失敗したステップがソルバープロファイラーで検出されない

陰的な可変ステップ連続ソルバー

問題がスティッフな場合は、陰的な可変ステップソルバーのいずれかを使用してみてください。

ode15s
ode23s
ode23t
ode23tb

ODE ソルバー	1 ステップ法	マルチステップ法	精度の次数	ソルバーリセットメソッド	最大次数	メソッド
`ode15s`		X	可変、低から中	X	X	数値微分式 (NDF)
`ode23s`	X		低			変更された 2 次の Rosenbrock 公式
`ode23t`	X		低	X		内挿を使用した台形則
`ode23tb`	X		低	X		TR-BDF2

ソルバーリセットメソッド

ode15s、ode23t、および ode23tb に対しては、[ソルバーのリセットメソッド] のドロップダウンメニューがコンフィギュレーションペインの [ソルバーの詳細] セクションに表示されます。このパラメーターは、たとえばゼロクロッシング検出などによって発生したリセットをソルバーが処理する方法を制御します。使用可能なオプションは、[高速] と [ロバスト] です。[高速] は、ソルバーがそのリセット時にヤコビアンを再計算しないことを指定し、[ロバスト] は再計算を指定します。結果として、[高速] 設定では計算は速くなりますが、場合によっては小さなステップサイズを使用することもあります。このような場合のテストでは、各設定を使用してシミュレーションを実行し、結果を比較します。結果に差が見られない場合は、[高速] 設定を問題なく使用して、時間を節約できます。結果が大きく異なる場合は、高速シミュレーションのステップサイズを削減してみてください。

最大次数

ode15s ソルバーに対しては、ソルバーが適用する数値微分式 (NDF) の最大次数を選択できます。ode15s では 1 次～ 5 次の方程式を使用するので、Maximum order パラメーターを使用して次数 1 ～ 5 を選択できます。スティッフな問題に対しては、2 次から始めてみてください。

陰的な可変ステップソルバーを選択するためのヒント

次の表は、陰的な可変ステップソルバーのアプリケーションに関するヒントをまとめています。これらのソルバーの動作を比較した例については、スティッフなモデルによる可変ステップソルバーの調査を参照してください。

ODE ソルバー	用途に関するヒント
ode15s	`ode15s` は、数値微分式 (NDF) に基づく可変次数ソルバーです。NDF は、後退差分式 (BDF) (Gear 法としても知られている) と関連していますが、より効率的です。`ode15s` ソルバーは、ヤコビ行列を数値的に生成します。問題がスティッフな場合、`ode45` がうまくいかない、または効率が非常に悪い場合には、`ode15s` を試してみてください。通常は、NDF の最大次数を 2 に制限することから始めてみてください。
ode23s	`ode23s` は、2 次の修正 Rosenbrock 公式に基づいています。この関数は、単段階ソルバーであるため、粗い許容範囲の場合には関数 `ode15s` よりも効率的な場合があります。`ode15s` 同様、`ode23s` はヤコビ行列を数値的に生成してくれます。ただし、`ode15s` では効果的でない特定のスティッフな問題を解くことができます。
ode23t	関数 `ode23t` ソルバーは、"フリー" 内挿を使用して台形則を実行します。問題が適度にスティッフで数値的減衰のない解が必要な場合に、このソルバーを使用してください (振動の動きのモデルを作成したときにエネルギーが放散されません。)
ode23tb	`ode23tb` は、2 つのステージをもつ陰的な Runge-Kutta 法である TR-BDF2 を実装したものです。最初のステージは台形則ステップで、2 番目のステージでは 2 次の後退差分式を使用します。この課程で、両方のステージの評価には同じ反復行列が使用されます。`ode23s` のように、このソルバーは大まかな許容誤差において `ode15s` より効率的な可能性があります。

メモ

スティッフな問題の場合、解は積分間隔に比して非常に短い時間スケールで変化する可能性がありますが、求めている解はそれよりはるかに長い時間スケールで変化します。スティッフな問題用に設計されていない手法は、可能な限り高速な変化を解くため十分に小さなタイムステップで計算を行うため、解がゆっくりと変化する区間に対しては効果的ではありません。詳細については、Shampine, L. F.、『Numerical Solution of Ordinary Differential Equations』、Chapman & Hall、1994 を参照してください。

可変ステップソルバーの許容誤差

局所誤差

可変ステップソルバーは、標準制御法を使用してタイムステップごとに局所誤差を監視します。各タイムステップの間、ソルバーはステップの終端で状態値を計算し、局所誤差、すなわちこれらの状態値の予測誤差も判別します。その後で、局所誤差を、相対的許容誤差 (rtol) と絶対的許容誤差 (atol) の関数である許容誤差と比較します。局所誤差が任意の状態に対する許容誤差より大きい場合には、ソルバーはステップサイズを小さくして再び試みます。

"相対許容誤差" は、各状態のサイズとの比較で誤差を測定します。相対的許容誤差は、状態の値の割合を表します。既定の 1e-3 は、計算された状態が 0.1% 以内の精度であることを意味します。
"絶対許容誤差" はしきい値誤差値です。この許容誤差は、測定された状態の値がゼロに近づくにつれて許容可能な誤差を表します。
ソルバーでは、i 番目の状態に対する誤差 e_i は、次式を満たす必要があります。

$e_{i} \leq \max (r t o l \times | x_{i} |, a t o l_{i}) .$

下の図は、状態のプロットと、相対的許容誤差と絶対的許容誤差が許容誤差を決める領域を示しています。

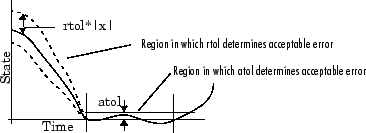
絶対許容誤差

モデルには、[コンフィギュレーションパラメーター] ダイアログボックスの [ソルバー] ペインで、グローバル絶対許容誤差を設定できます。この許容誤差モデルのすべての状態に適用されます。auto または実数スカラーを指定できます。auto (既定) を指定すると、Simulink は各状態に対する絶対許容誤差を、相対許容誤差に基づいて初期設定します。相対許容誤差が 1e-3 より大きい場合、abstol は 1e-6 に初期設定されます。ただし、reltol が 1e-3 より小さい場合、その状態に対する abstol は reltol * 1e-3 に初期設定されます。シミュレーションが進行すると、各状態に対する絶対許容誤差は、その時点までの状態の最大値に、その状態の相対許容誤差を掛け合わせたものに再設定されます。したがって、状態が 0 から 1 に変化し reltol が 1e-3 の場合は、abstol は 1e-6 に初期設定され、シミュレーションの終わりには 1e-3 になります。状態が 0 から 1000 に変化した場合、abstol は 1 に変更されます。

ここで、状態が 0 から 1 に変化し、reltol が 1e-4 に設定されている場合、abstol は 1e-7 に初期設定され、シミュレーションの終わりには 1e-4 の値になります。

絶対的許容誤差の初期値の計算結果が適切でない場合、自分で適切な値を指定することができます。絶対的許容誤差に対する適切な値を決定するには、シミュレーションを複数回実行する必要があります。また、AutoScaleAbsTol パラメーターの有効または無効を切り替えることによって、絶対許容誤差も同様にその [自動] 設定に適応するかどうかを指定できます。詳細については、Auto scale absolute toleranceを参照してください。

一部のブロックでは、計算したり出力を定義したりするモデルの状態を解くために絶対許容誤差の値を指定できます。

これらのブロックに対してユーザーが指定した絶対許容誤差値は、[コンフィギュレーションパラメーター] ダイアログボックスでのグローバル設定値をオーバーライドします。たとえば、モデルの状態が大きく変化するなどの理由のため、グローバル設定値ではすべてのモデル状態のエラー制御が十分にできない場合は、グローバル設定値をオーバーライドできます。ブロックの絶対許容誤差値は次の値に設定できます。

auto
–1 ( auto に同じ)
positive scalar
real vector (ブロック内の対応する連続状態の数と同じ次元)

ヒント

絶対許容誤差を設定する場合、低すぎる値を設定すると状態値のゼロ近辺でのソルバーのステップ数が多くなりすぎるため注意が必要です。結果的に、シミュレーションの速度が低下します。

反対に、高すぎる絶対許容誤差を設定した場合には、モデル内の 1 つ以上の連続状態がゼロに近づくにつれて、結果の精度が低くなる可能性があります。

シミュレーションが完了した後に、絶対許容誤差を低くして再度シミュレーションを実行することによって、結果の精度を検証できます。2 回のシミュレーションの結果が大幅に異なっていなければ、十分な精度が得られていると考えられます。