Main Content

スティッフなモデルによる可変ステップ ソルバーの調査

この例では次を使用します。

モデルを開く

この例では、フーコーの振子モデルの可変ステップ ソルバーの動作を示します。Simulink® ソルバー ode45、ode15s、ode23 および ode23t がテスト ケースとして使用されます。スティッフな微分方程式が、この問題を解くために使用されます。方程式のスティッフ性の厳密な定義は存在しません。数値的手法を使用してスティッフな方程式を解く場合、一部の数値的手法は不安定なため、ステップ サイズをかなり小さくしなければ、スティッフな問題に対する数値的に安定した解を得ることができません。スティッフな問題には、すぐに変化する要素と、ゆっくりと変化する要素が含まれていることがあります。

フーコーの振子は、スティッフな問題の一例です。振子が 2 ～ 3 秒で振動を終える (すぐに変化する要素) のに対し、地球が 1 回自転するのには 1 日かかります (ゆっくりと変化する要素)。振子の振動面は、地球の自転のため、ゆっくりと回転します。フーコーの振子の物理的作用の詳細については、フーコーの振子のモデル化を参照してください。

シミュレーションにより、地球上の観測者から見た x-y 平面における振子の振り玉の位置が計算されます。次に、振子のエネルギーの総量が計算され、さまざまな Simulink ソルバーの性能の評価に使用されます。

フーコーの振子モデル

フーコーの振子は、以下に示す連立微分方程式系で説明されます。摩擦と空気抵抗は考慮されません (考慮しないことで方程式が大幅に単純化されます)。これらの方程式の全微分を、フーコーの振子の例で示します。

$$ \ddot{x} = 2\Omega \sin{\lambda} \dot{y} - \frac{g}{L} x $$

$$ \ddot{y} = - 2\Omega\sin{\lambda} \dot{x} - \frac{g}{L} y $$

$$\Omega = \mbox{ Earth's angular velocity of rotation around its axis}$$

$$\lambda = \mbox{ geographic latitude}$$

$$g = \mbox{ acceleration of gravity}$$

$$x \mbox{ and } y = \mbox{ coordinates of the pendulum bob}$$

モデル sldemo_solvers は、フーコーの振子を説明する微分方程式を解くために使用されています。この例では、フーコーの振子が 86,400 秒間シミュレートされます。制約と初期条件は、モデル ワークスペースに保存されます。

可変ステップ ソルバー

この例では、ode45、ode15s、ode23 および ode23t 可変ステップ ソルバーの性能を調べます。

ソルバーの性能の評価

ソルバーの性能を評価するにはさまざまな方法があります。問題が閉じた形の解をもつ場合は、ソルバーの結果を、期待される理論上の結果と比較できます。特定のソルバーを使用して、モデルのシミュレーションの所要時間をモニターすることもできます。

残念ながら、フーコーの振子には厳密な理論解がありません。閉じた形の近似解はあります。ただし、閉じた形の近似解はソルバーの性能の評価には使用できません (フーコーの振子の例を参照)。

エネルギーの総量の保存

この例では、エネルギー保存の法則を検証することによってソルバーの性能を評価します。摩擦のない環境では、振子のエネルギーの総量は一定に保たれるはずです。しかし、振子のエネルギーの計算値は一定ではありません。これは、数値の精度が限られているためです。

この例では、振子の正規化エネルギーの総量が、タイム ステップごとに計算されます。エネルギーの相対誤差は、シミュレーション中のエネルギーの総量の変化に等しくなります。エネルギーは保存されるため、理想的には、エネルギーの相対誤差はゼロでなければなりません。エネルギーの総量は、位置エネルギーと運動エネルギーの和です。NormalizeEnergy ブロックでは、振子の正規化エネルギーが次の方程式を使用して計算されます。

$$ E = \frac{v_x^2 + v_y^2}{2} + g( L - \sqrt{L^2 - x^2 - y^2} ) $$

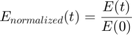
$$E_{normalized}(t) = \frac{E(t)}{E(0)}$$

$$E(0) = \mbox{ initial total energy}$$

このプロットは、ode23 と ode23t を使用して計算された、時間に対する正規化エネルギーを示したものです。この問題に関しては、ode23t の方が ode23 よりもはるかに正確です。ode23 を使用したシミュレーションでは、振子の正規化エネルギーが 60% より多く減少しました。振子のもつエネルギーが小さいと、振動振幅も小さくなります。この影響は次のプロットを見るとわかります。ode23 で計算された振子の振幅は、振動面が回転すると小さくなっています。

これらのプロットは、スティッフ ソルバーとノンスティッフ ソルバーの違いを示しています。各プロットは、1 日のうちの振子の振り玉の位置を示しています。データ点は 15 番目ごとに青色でプロットされています。黒い点は振子の振り玉の初期位置を示し、青い線は振子の初期振動面を示します。赤い線は 1 日の終わりの振動面を示します。黄色の線は中間時点における振動面を示します。振子の振動面が 1 周するには、1 日では足りません。振動面の回転の速さは、地理緯度によって異なります (フーコーの振子の例を参照)。左のプロットでは振子の振幅は小さくなっているのに対し、右のプロットでは振幅は一定です。相対許容誤差が 1e-5 で同じ場合、スティッフ ソルバーの方が結果の精度は高くなりますが、実行時間が長くなります。

次のプロットでは、Simulink ソルバーの性能をさらに詳しく調べています。4 つのソルバーを選び、相対許容誤差の関数としての相対誤差と実行時間の変動を示しています。ソルバーをより広範囲にテストするなら、スクリプト sldemo_solvers_mcode.m を使用できます。このスクリプトを使用すると、シミュレーションをスピードアップし、数分で実行できる C コードがモデルから生成されます。

Building RSim executable for model..
Time taken: 13.530949 seconds.

Running generated RSim executable..
Time taken: 197.034259 seconds.

この例では、相対許容誤差が 1e-6 未満の場合に相対誤差があまり減少していません。これは、特定のモデルに依存する数値ソルバーの限界です。ソルバーの相対許容誤差を小さくしたからといって、精度が上がるとは限りません。問題に必要な最低限の精度を推定し、シミュレーション コストとのバランスを考慮してソルバーを選択する必要があります。たとえば、フーコーの振子の振り玉の位置を数センチの範囲内で知りたいとします。その場合は、振子の位置を数ミクロンの範囲内で計算する必要はありません。そこまで正確に測定することはできないからです。

シミュレーションの数値結果と動作は、ソルバーの設定によって異なる場合があります。スティッフな問題の場合、これは非常に重要な意味をもちます。スティッフなモデルを扱う場合は、少ない計算コストで正確な結果を出すソルバーを選択してください。可変ステップ ソルバーの相対許容誤差または固定ステップ ソルバーのステップ サイズを十分に小さくし、数値的に安定した結果が得られるようにする必要があります。ソルバーの中には特に効率的なものもありますが、スティッフな問題により適しているのはスティッフ ソルバーです。可変ステップ ソルバーは、固定ステップ ソルバーよりもロバストです。