荷重制約をもつ 2 つのシリンダーのモデル

モデルを開く

この例では、2 つの油圧アクチュエータを相互に接続する、大きな質量を支える剛体棒をモデル化する方法を示します。ピストンの力が荷重に直接かかるため、このモデルではバネは使用されません。これらの力は重力と釣り合うため、線形変位と回転変位の両方が発生します。

モデルの解析と物理現象

棒の回転角はわずかです。棒の運動の方程式は、以下の方程式セット 1 で与えられています。シリンダーとポンプの動作を説明する方程式は、1 つのシリンダーの例の場合と同じです。

方程式セット 1:

$$M \frac{d^2 z}{d t^2} = F_b + F_a + F_{ext} $$

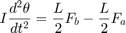
$$I \frac{d^2 \theta}{d t^2} = \frac{L}{2}F_b - \frac{L}{2}F_a $$

$$ z - \mbox{ displacement at the center } $$

$$ M - \mbox{ total mass } $$

$$ F_a - \mbox{ piston A force } $$

$$ F_b - \mbox{ piston B force } $$

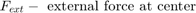
$$ F_{ext} - \mbox{ external force at center } $$

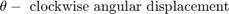
$$ \theta - \mbox{ clockwise angular displacement } $$

$$ I - \mbox{ moment of inertia of the rod } $$

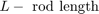
$$ L - \mbox{ rod length } $$

個々のピストンの位置と速度は、形状から直接得られます。対応する方程式を、方程式セット 2 で確認してください。

方程式セット 2:

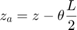
$$ z_a = z - \theta \frac{L}{2} $$

$$ z_b = z + \theta \frac{L}{2} $$

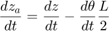
$$ \frac{d z_a}{dt} = \frac{d z}{dt} - \frac{d \theta}{dt} \frac{L}{2} $$

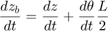
$$ \frac{d z_b}{dt} = \frac{d z}{dt} + \frac{d \theta}{dt} \frac{L}{2} $$

$$ z_a - \mbox{ piston A displacement } $$

$$ z_b - \mbox{ piston B displacement } $$

モデルを開いてシミュレーションを実行

このモデルを開くには、コマンドを「sldemo_hydrod」と入力します。シミュレーションを実行するには、[シミュレーション] ツールストリップで [実行] をクリックします。モデルは以下を実行します。

  • 信号データのログを MATLAB® ワークスペースの Simulink.SimulationOutput オブジェクト out に記録します。信号のログ データは sldemo_hydrod_output という Simulink.SimulationData.Dataset オブジェクトの out 内に格納されます。

  • 連続状態データのログを MATLAB ワークスペースに記録します。状態データは、xout と呼ばれる構造体として out ワークスペース変数にも含まれます。ログ データの処理に役立つように、各状態にモデル内で名前が割り当てられます。状態の名前は、xout.signals の stateName フィールドにあります。詳細については、記録されたシミュレーション データのデータ形式を参照してください。

  • カスタマイズ可能な Circular GaugeブロックとVertical Gaugeブロックを使用して、シリンダー内の流体の流れ、圧力、および線形変位を可視化します。

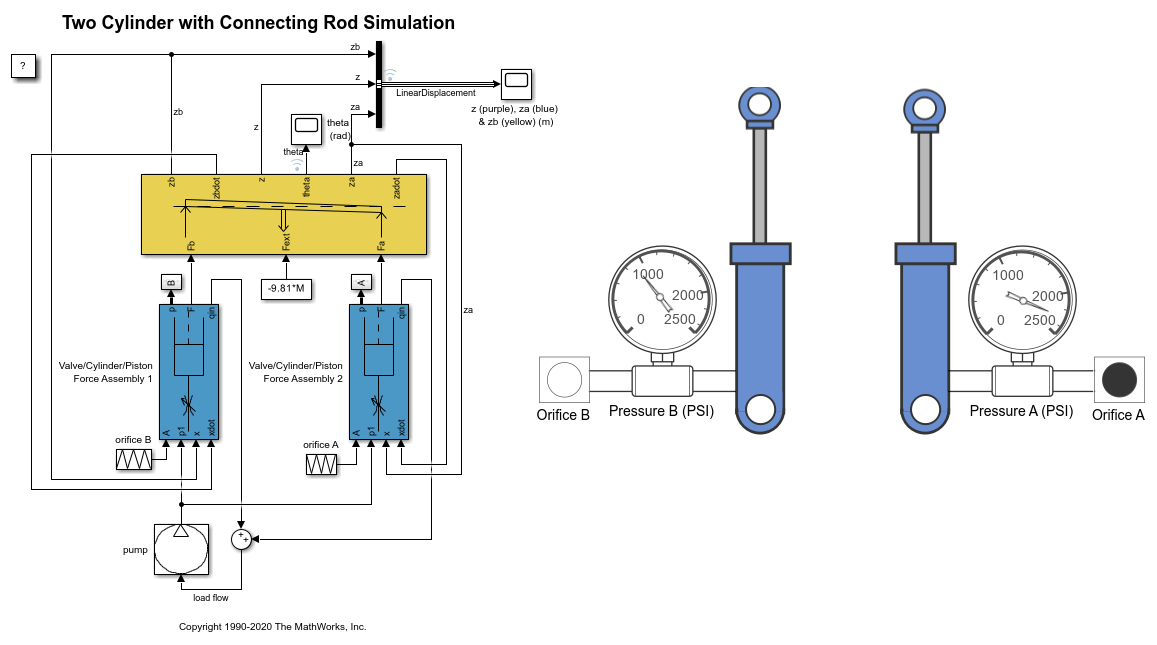
Mechanical Load サブシステム

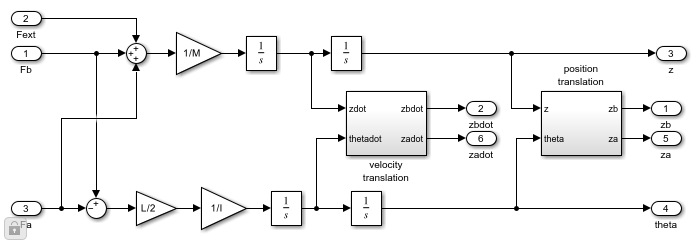
Mechanical Load サブシステムは、標準の Simulink ブロックを使用して直接計算される運動の方程式を解きます。回転角は小さいと仮定されています。Mechanical Load サブシステムのマスクの中を調べ、その構造を確認するには、サブシステムを右クリックし、[マスク]、[マスク内を表示] を選択します。

シミュレーション パラメーター

このシミュレーションで使用されるパラメーターは、以下を除き、1 つの油圧シリンダーのシミュレーションのモデルで使用されるものと同じです。

L     = 1.5 m
M     = 2500 kg
I     = 100 kg/m^2
Qmax = 0.005 m^3/sec (constant)
C2    = 3e-9 m^3/sec/Pa
Fext  = -9.81*M Newtons

ポンプ流量は一定ですが、バルブは個別に制御されます。最初に、t = 0 ではバルブ B の断面積はゼロです。値は線形に増加して t = 0.01 sec で 1.2e-5 m^2 になり、その後は線形に減少して t = 0.02 sec でゼロになります。バルブ A の断面積は t = 0 では 1.2e-5 sq.m. です。値は線形に減少して t = 0.01 sec でゼロになり、その後は線形に増加して t = 0.02 sec で 1.2e-5 sq.m になります。その後、バルブ A および B の動作は、同じパターンで周期的に繰り返されます。つまり、バルブ A とバルブ B は位相が 180 度ずれています。

結果

以下のプロットは、棒の線形変位と角変位を示しています。線形変位応答は、タイプ 1 の積分系に典型的にみられます。棒の相対位置と角運動は、位相のずれた制御信号に対する 2 つのピストンの応答、つまりバルブ A および B の断面積を示しています。

参考

|

トピック