このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

edr

実信号での編集距離

構文

dist = edr(x,y,tol)

[dist,ix,iy] = edr(x,y,tol)

[___] = edr(x,y,maxsamp)

[___] = edr(___,metric)

edr(___)

説明

dist = edr(x,y,tol) は、シーケンス x および y 間の実信号での編集距離を返します。edr は、x、y、または x と y の両方から削除する必要がある要素の最小数を返して、残りの信号要素間のユークリッド距離の合計が指定許容誤差 tol 内に収まるようにします。

[dist,ix,iy] = edr(x,y,tol) は、x(ix) および y(iy) 間の dist が可能な限り最小となるワーピング パスを返します。x と y が行列の場合、ix と iy は x(:,ix) と y(:,iy) の分離間隔が最小限となる値になります。

[___] = edr(x,y,maxsamp) は、ワーピング パスが x と y 間の直線近似の maxsamp のサンプル数内に入るように挿入操作を制限します。この構文は、前述の構文の出力引数のいずれかを返します。

[___] = edr(___,metric) は、前述の構文の任意の入力引数に加えて使用する距離計量を指定します。metric は、'euclidean'、'absolute'、'squared'、または 'symmkl' のいずれかになります。

出力引数を指定しない edr(___) は、元の信号と整列後の信号をプロットします。

• 信号が実数ベクトルの場合、関数は元の 2 つの信号を 1 つのサブプロットに表示し、整列後の信号をその下のサブプロットに表示します。

• 信号が複素数ベクトルの場合、関数は元の信号と整列後の信号を 3 次元プロットに表示します。

• 信号が実数行列の場合、関数は imagesc を使用して元の信号と整列後の信号を表示します。

• 信号が複素行列の場合、関数は実数部と虚数部を各イメージの上半分と下半分にプロットします。

例

外れ値があるチャープおよび正弦波の間の編集距離

チャープと正弦波の 2 つの実信号を生成します。それぞれの信号に明らかに値が外れているセクションを追加します。

x = cos(2*pi*(3*(1:1000)/1000).^2);
y = cos(2*pi*9*(1:399)/400);

x(400:410) = 7;
y(100:115) = 7;

信号間の編集距離が最小となるように信号を歪めます。許容誤差には 0.1 を指定します。整列された信号をワーピングの前と後の両方についてプロットし、その間の距離を出力します。

tol = 0.1;
edr(x,y,tol)

ans = 617

正弦波周波数を初期値の 2 倍に変更します。計算を繰り返します。

y = cos(2*pi*18*(1:399)/400);
y(100:115) = 7;

edr(x,y,tol);

各信号に虚数部を追加します。初期の正弦波周波数に戻します。ユークリッド距離の二乗和を最小化することによって信号を整列します。

x = exp(2i*pi*(3*(1:1000)/1000).^2);
y = exp(2i*pi*9*(1:399)/400);

x(400:405) = 5+3j;
x(405:410) = 7;

y(100:107) = 3j;
y(108:115) = 7-3j;

edr(x,y,tol,'squared');

編集距離とワーピング パス

異なる長さの谷で隔てられた 2 つの明確なピークから構成される信号を 2 つ生成します。信号をプロットします。

x1 = [0 1 0 1 0]*.95;
x2 = [0 1 0 0 0 0 0 0 0 0 1 0]*.95;

subplot(2,1,1)
plot(x1)
xlim([0 12])
subplot(2,1,2)
plot(x2)
xlim([0 12])

信号間の編集距離を計算します。等しいサンプルどうしのみが一致するように許容誤差に小さな値を設定します。

tol = 0.1;

figure
edr(x1,x2,tol);

信号間の距離は 7 です。これらを揃えるには、x2 の中央にある 7 つのゼロを削除するか、x1 に 7 つのゼロを追加する必要があります。

D 行列を計算します。右の一番下の要素は、編集距離に対応します。D の定義については、実信号での編集距離を参照してください。

cnd = (abs(x1'-x2))>tol;
D = zeros(length(x1)+1,length(x2)+1);
D(1,2:end) = 1:length(x2);
D(2:end,1) = 1:length(x1);

for h = 2:length(x1)+1
    for k = 2:length(x2)+1
        D(h,k) = min([D(h-1,k)+1 ...
            D(h,k-1)+1 ...
            D(h-1,k-1)+cnd(h-1,k-1)]);
    end
end

D

D = 6×13

     0     1     2     3     4     5     6     7     8     9    10    11    12
     1     0     1     2     3     4     5     6     7     8     9    10    11
     2     1     0     1     2     3     4     5     6     7     8     9    10
     3     2     1     0     1     2     3     4     5     6     7     8     9
     4     3     2     1     1     2     3     4     5     6     7     7     8
     5     4     3     2     1     1     2     3     4     5     6     7     7

信号を揃えるワーピング パスを計算および表示します。

[d,i1,i2] = edr(x1,x2,tol);

E = zeros(length(x1),length(x2));

for k = 1:length(i1)
    E(i1(k),i2(k)) = NaN;
end

E

E = 5×12

   NaN     0     0     0     0     0     0     0     0     0     0     0
     0   NaN     0     0     0     0     0     0     0     0     0     0
     0     0   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN     0     0
     0     0     0     0     0     0     0     0     0     0   NaN     0
     0     0     0     0     0     0     0     0     0     0     0   NaN

計算を繰り返しますが、今度は、対角線から逸脱する要素が 2 つまでになるようにワーピング パスに制約を付けます。引き伸ばした信号とワーピング パスをプロットします。2 番目のプロットで、x 軸に沿って実行する行列の列を設定します。

[dc,i1c,i2c] = edr(x1,x2,tol,2);

subplot(2,1,1)
plot([x1(i1c);x2(i2c)]','.-')
title(['Distance: ' num2str(dc)])
subplot(2,1,2)
plot(i2c,i1c,'o-',[i2(1) i2(end)],[i1(1) i1(end)])
axis ij
title('Warping Path')

この制約により、編集距離は小さくなりますが、信号が歪みます。制約を満たすことができない場合、edr は、距離に対して NaN を返します。対角線からの逸脱が最大でも 1 要素になるようにワーピング パスが強制されていることがわかります。

[dc,i1c,i2c] = edr(x1,x2,tol,1);

subplot(2,1,1)
plot([x1(i1c);x2(i2c)]','.-')
title(['Distance: ' num2str(dc)])
subplot(2,1,2)
plot(i2c,i1c,'o-',[i2(1) i2(end)],[i1(1) i1(end)])
axis ij
title('Warping Path')

汚れた手書き文字サンプルの位置合わせ

ファイル MATLAB1.gif と MATLAB2.gif には、"MATLAB®" という単語の 2 つの手書き文字のサンプルが含まれています。ファイルを読み込みます。データに汚れを付けて外れ値を追加します。

samp1 = 'MATLAB1.gif';
samp2 = 'MATLAB2.gif';

x = double(imread(samp1));
y = double(imread(samp2));

x(15:20,54:60) = 4000;
y(15:20,84:96) = 4000;

編集距離を使用して x 軸に沿って手書きサンプルの位置を合わせます。許容誤差には 450 を指定します。

edr(x,y,450);

入力引数

x — 入力信号

ベクトル | 行列

実数または複素数のベクトルまたは行列として指定される入力信号。

データ型: single | double
複素数のサポート: あり

y — 入力信号

ベクトル | 行列

実数または複素数のベクトルまたは行列として指定される入力信号。

データ型: single | double
複素数のサポート: あり

tol — 許容誤差

正のスカラー

許容誤差。正のスカラーで指定します。

データ型: single | double

maxsamp — 調整ウィンドウの幅

Inf (既定値) | 正の整数

調整ウィンドウの幅。正の整数で指定します。

データ型: single | double

metric — 距離計量

'euclidean' (既定値) | 'absolute' | 'squared' | 'symmkl'

距離計量。'euclidean'、'absolute'、'squared'、または 'symmkl' で指定します。X と Y が両方とも K 次元の信号である場合、metric は X の m 番目のサンプルと Y の n 番目のサンプルの間の距離 d_mn(X,Y) を規定します。

• 'euclidean' — 距離の二乗和根。ユークリッド計量または ℓ₂ 計量とも呼ばれます。

  $$d_{mn}(X,Y)=\sqrt{{\displaystyle \sum _{k=1}^K{\left(x_{k,m}-y_{k,n}\right)}^{*}\left(x_{k,m}-y_{k,n}\right)}}$$

• 'absolute' — 差の絶対値の総和。マンハッタン計量、街区計量、タクシー計量または ℓ₁ 計量とも呼ばれます。

  $$d_{mn}(X,Y)={\displaystyle \sum _{k=1}^K\left|x_{k,m}-y_{k,n}\right|}={\displaystyle \sum _{k=1}^K\sqrt{{\left(x_{k,m}-y_{k,n}\right)}^{*}\left(x_{k,m}-y_{k,n}\right)}}$$

• 'squared' — ユークリッド計量の 2 乗。距離の二乗和で構成されます。

  $$d_{mn}(X,Y)={\displaystyle \sum _{k=1}^K{\left(x_{k,m}-y_{k,n}\right)}^{*}\left(x_{k,m}-y_{k,n}\right)}$$

• 'symmkl' — 対称カルバック・ライブラー距離。この計量は、正の実数の X と Y に対してのみ有効です。

  $$d_{mn}(X,Y)={\displaystyle \sum _{k=1}^K\left(x_{k,m}-y_{k,n}\right)\left(\log x_{k,m}-\log y_{k,n}\right)}$$

出力引数

dist — 最小距離

正の実数のスカラー

信号間の最小距離。正の実数のスカラーとして返されます。

ix,iy — ワーピング パス

インデックスのベクトル

ワーピング パス。インデックスのベクトルとして返されます。ix と iy は同じ長さです。各ベクトルは単調増加数列を含み、その数列に基づいて、対応する信号 x または y の要素に対するインデックスが必要な回数だけ繰り返されます。

詳細

実信号での編集距離

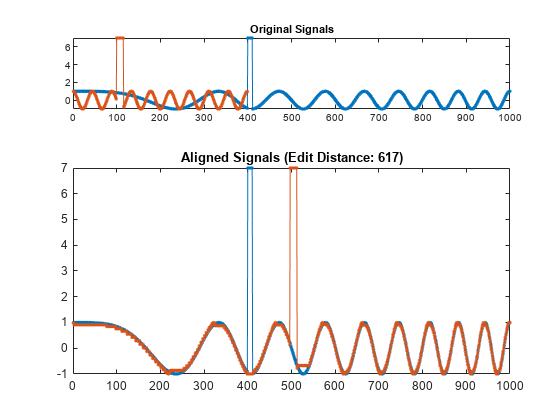
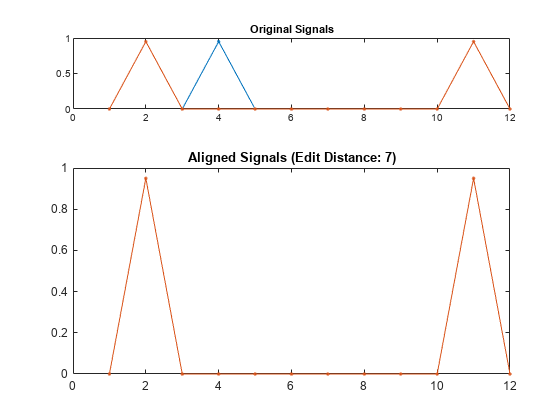
同じ順序に並んだ同等の特徴をもつ 2 つの信号が、セクションの持続時間の違いによって大きく異なって見える場合があります。edr はこれらの持続時間を歪ませて、対応する特徴が共通の時間軸上の同じ位置に現れるようにさせ、信号間の類似点を強調します。歪みを実行するために使用される基準は、外れ値に対してロバストになるように設計されています。

次の 2 つの K 次元信号を考えます。

$$X=\left[\begin{array}{cccc}{x}_{1,1}& x_{1,2}& \cdots & x_{1,M}\\ x_{2,1}& x_{2,2}& \cdots & x_{2,M}\\ ⋮& ⋮& \ddots & ⋮\\ x_{K,1}& x_{K,2}& \cdots & x_{K,M}\end{array}\right]$$

および

$$Y=\left[\begin{array}{cccc}{y}_{1,1}& y_{1,2}& \cdots & y_{1,N}\\ y_{2,1}& y_{2,2}& \cdots & y_{2,N}\\ ⋮& ⋮& \ddots & ⋮\\ y_{K,1}& y_{K,2}& \cdots & y_{K,N}\end{array}\right],$$

これらの信号には、それぞれ M 個と N 個のサンプルがあります。metric で指定された X の m 番目のサンプルと Y の n 番目のサンプルの間の距離 d_mn(X,Y) が与えられた場合、関数 edr は X と Y を、信号間の "編集距離" が最小となる時点の共通集合上で引き伸ばします。

tol に指定された許容誤差である実数 ε が与えられたとき、d_mn(X,Y) < ε の場合に X の m 番目のサンプルと Y の n 番目のサンプルが "一致する" ことを宣言します。2 つのサンプルの m と n が一致しない場合には、次の 3 つの方法のいずれかでそれらを一致させることができます。

1. 次のサンプルが n に一致する場合などは、最初の信号から m を削除します。この削除は、m を 2 つ目の信号に追加して、2 つの連続一致を得ることと等価です。

2. n に一致するサンプルを適切な位置に追加し、残りのサンプルの位置を 1 つ移動することにより、最初の信号の長さを引き伸ばします。この追加は、一致しない n を 2 つ目の信号から削除することと等価です。

3. 最初の信号で m に n を代入します。または、同等の操作として、m と n の両方を削除します。

編集距離は、2 つの信号を一致させるために必要なこれらの操作の合計数です。この数値は一意ではありません。X と Y 間の編集距離ができるだけ小さくなるように計算するには、次の事実に基づいて開始します。

1. 2 つの空の信号間の距離は、ゼロです。

2. 空の信号と L 個のサンプルをもつ信号間の距離は L です。これは、他の信号を復元するために、空の信号に追加する必要があるサンプル数であるためです。これはすなわち、L は L サンプル信号を空にするために削除しなければならないサンプルの数ということです。

次のように (M + 1) 行 (N + 1) 列の行列 D を作成します。

1. D_1,1 = 0.

2. D_m,1 = m – 1 (m = 2, …, M + 1)

3. D_1,n = n – 1 (n = 2, …, N + 1)

4. m, n > 1 の場合、

   $$D_{m,n}=\min \left\{\begin{array}{c}{D}_{m-1,n}+1\\ D_{m,n-1}+1\\ D_{m-1,n-1}+\{\begin{array}{c}0\Leftarrow d_{m,n}(X,Y)\le \epsilon \\ 1\Leftarrow d_{m,n}(X,Y)>\epsilon \end{array}\end{array}\right\}.$$

したがって、X と Y 間の最小の編集距離は、D_M+1,N+1 となります。

この編集距離が最小となる D 経由の "ワーピング パス" は、次のように、同じ長さの 2 つのシーケンス ix および iy によってパラメーター化され、"チェスのキング" の動きの組み合わせになります。

• 垂直方向の動き: (m,n) → (m + 1,n) は、X からのサンプルの削除、または Y へのサンプルの追加に対応します。それぞれの移動では、編集距離が 1 増えます。

• 水平方向の動き: (m,n) → (m,n + 1) は、Y からのサンプルの削除、または X へのサンプルの追加に対応します。それぞれの移動では、編集距離が 1 増えます。

• 対角方向の動き: (m,n) → (m + 1,n + 1) は、d_m,n(X,Y) ≤ ε の場合は一致に対応、d_m,n(X,Y) > ε の場合は各信号からの 1 サンプル削除に対応します。一致による距離の増加はありません。削除では 1 増えます。

この構造では、条件に合うパスがいずれも、サンプルをスキップしたり、信号の特徴を反復したりせず、すべての信号を揃えることが確保されます。さらに、望ましいパスは、d_1,1(X,Y) と d_M,N(X,Y) の間に伸びる対角方向のラインの近くを通ります。maxsamp 引数で調整されるこの追加の制約により、長さが類似するセクションのワーピングによる比較が必ず行われます。

2 つのサンプルを一致させるためのペナルティは、サンプル間の値の違いとは無関係です。許容誤差をわずかに超える差がある 2 つのサンプルが、その差が著しい 2 つのサンプルと同じペナルティを受けます。そのため、編集距離は外れ値の影響を受けません。一方、2 つの信号を揃えるためにサンプルを繰り返すことにはコストがかかります。これは動的タイム ワーピングの場合は該当しません。

参照

[1] Chen, Lei, M. Tamer Özsu, and Vincent Oria. "Robust and Fast Similarity Search for Moving Object Trajectories." Proceedings of 24th ACM International Conference on Management of Data (SIGMOD ‘05). 2005, pp. 491–502.

[2] Paliwal, K. K., Anant Agarwal, and Sarvajit S. Sinha. "A Modification over Sakoe and Chiba’s Dynamic Time Warping Algorithm for Isolated Word Recognition." Signal Processing. Vol. 4, 1982, pp. 329–333.

[3] Sakoe, Hiroaki, and Seibi Chiba. "Dynamic Programming Algorithm Optimization for Spoken Word Recognition." IEEE^® Transactions on Acoustics, Speech, and Signal Processing. Vol. ASSP-26, No. 1, 1978, pp. 43–49.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2016b で導入

参考

alignsignals | dtw | finddelay | findsignal | xcorr