Train Reinforcement Learning Policy Using Custom Training Loop
This example shows how to define a custom training loop for a reinforcement learning policy. You can use this workflow to train reinforcement learning policies with your own custom training algorithms rather than using one of the built-in agents from the Reinforcement Learning Toolbox™ software.
Using this workflow, you can train policies that use any of the following policy and value function approximators.
rlValueFunction- State value function approximatorrlQValueFunction- State-action value function approximator with scalar outputrlVectorQValueFunction- State-action function approximator with vector outputrlContinuousDeterministicActor- Continuous deterministic actorrlDiscreteCategoricalActor- Discrete stochastic actorrlContinuousGaussianActor- Continuous Gaussian actor (stochastic)
In this example, a discrete actor policy with a discrete action space is trained using the REINFORCE algorithm (with no baseline). For more information on the REINFORCE algorithm, see REINFORCE Policy Gradient (PG) Agent.
For more information on the functions you can use for custom training, see Functions for Custom Training.
Fix Random Number Stream for Reproducibility
The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility. Fix the random number stream with seed 0 and random number algorithm Mersenne twister. For more information on controlling the seed used for random number generation, see rng.
previousRngState = rng(0,"twister");The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.
Environment
For this example, a reinforcement learning policy is trained in a discrete cart-pole environment. The objective in this environment is to balance the pole by applying forces (actions) on the cart. Create the environment using the rlPredefinedEnv function.
env = rlPredefinedEnv("CartPole-Discrete");Extract the observation and action specifications from the environment.
obsInfo = getObservationInfo(env); actInfo = getActionInfo(env);
Obtain the dimension of the observation space (numObs) and the number of possible actions (numAct).
numObs = obsInfo.Dimension(1); numAct = actInfo.Dimension(1);
For more information on this environment, see Load Predefined Control System Environments.
Policy
The reinforcement learning policy in this example is a discrete-action stochastic policy. It is modeled by a deep neural network that contains fullyConnectedLayer, reluLayer, and softmaxLayer layers. This network outputs probabilities for each discrete action given the current observations. The softmaxLayer ensures that the actor outputs probability values in the range [0 1] and that all probabilities sum to 1.
Create the deep neural network for the actor.
actorNetwork = [
featureInputLayer(numObs)
fullyConnectedLayer(24)
reluLayer
fullyConnectedLayer(24)
reluLayer
fullyConnectedLayer(2)
softmaxLayer
];Convert to dlnetwork. For more information, see dlaccelerate.
actorNetwork = dlnetwork(actorNetwork);
Create the actor using an rlDiscreteCategoricalActor object.
actor = rlDiscreteCategoricalActor(actorNetwork,obsInfo,actInfo);
Accelerate the gradient computation of the actor.
actorGradFcn = dlaccelerate(@actorLossFunction);
Evaluate the policy with a random observation as input.
policyEvalOutCell = evaluate(actor,{rand(obsInfo.Dimension)});
policyEvalOut = policyEvalOutCell{1}policyEvalOut = 2×1 single column vector
0.4682
0.5318
Create a noisy policy from the actor.
policy = rlStochasticActorPolicy(actor);
Create the optimizer using rlOptimizer and rlOptimizerOptions function.
optimOpt = rlOptimizerOptions(LearnRate=5e-3,GradientThreshold=1); actorOptimizer = rlOptimizer(optimOpt);
Training Setup
Configure the training to use the following options:
Set up the training to last at most 5000 episodes, with each episode lasting at most 250 steps.
To calculate the discounted reward, choose a discount factor of 0.995.
Terminate the training after the maximum number of episodes is reached or when the average reward across 100 episodes reaches the value of 220.
numEpisodes = 5000; maxStepsPerEpisode = 250; discountFactor = 0.995; avgWindowSize = 100; trainingTerminationValue = 220;
Create a vector to store the cumulative reward for each training episode.
episodeCumulativeRewardVector = [];
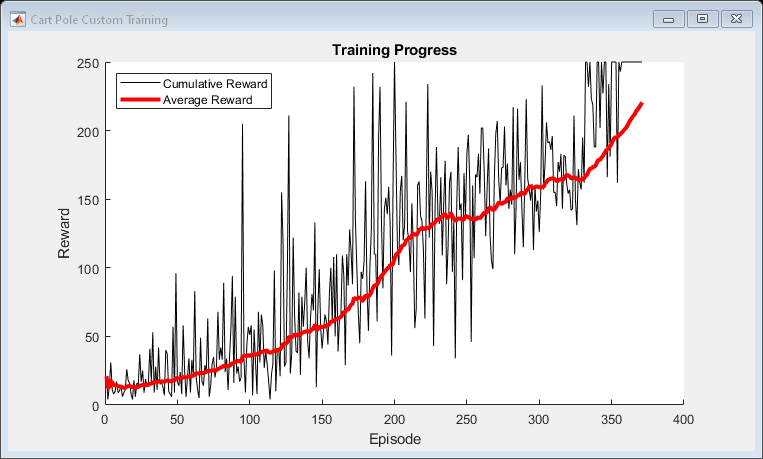
Create a figure for training visualization using the hBuildFigure helper function.
[trainingPlot,lineReward,lineAveReward] = hBuildFigure;
Custom Training Loop
Fix the random stream for reproducibility.
rng(0,"twister");The algorithm for the custom training loop is as follows. For each episode:
Create aggregated trajectory data buffers for storing experience information: observations, actions, and rewards.
Reset the environment.
Generate experiences until a terminal condition occurs. To do so, evaluate the policy to get actions, apply those actions to the environment, and obtain the resulting observations and rewards. Store the actions, observations, and rewards in buffers.
Compute the episode Monte Carlo return, which is the discounted future reward.
Compute the gradient of the loss function with respect to the policy parameters.
Update the actor using the computed gradients.
Update the training visualization.
Terminate training if the policy is sufficiently trained.
Enable the training visualization plot.
set(trainingPlot,Visible="on");
Create buffers for the training data, allocating enough data for 5 full episodes. Learning occurs after each 5th episode finishes. Aggregating multiple trajectories for on-policy learning can improve training convergence.
trajectoriesForLearning = 5;
Buffers are allocated as dlarray objects to support automatic differentiation with dlfeval and dlgradient.
buffLen = trajectoriesForLearning*maxStepsPerEpisode; observationBuffer = dlarray(zeros(numObs,1,buffLen));
Allocate valid actions for the action buffer.
actionBuffer = dlarray( ...
zeros(numAct,1,buffLen) + actInfo.Elements(1));
rewardBuffer = dlarray(zeros(1,buffLen));
returnBuffer = dlarray(zeros(1,buffLen));
Create a "mask" variable to ensure that we are using consistent batch sizes for every gradient computation. The mask is used to set to zero advantages in the loss function for experiences beyond the actual number of steps taken in any given simulation. This ensures that additional accelerated functions are not generated for the actor loss function.
% mask(i) == 1 for i <= batchSize % mask(i) == 0 for i > batchSize maskBuffer = dlarray(zeros(1,buffLen)); actionSet = repmat(actInfo.Elements',1,buffLen);
Create a weighted discount matrix based on the maximum episode length. This will be used to compute discountedReturn before learning.
v = 0:(maxStepsPerEpisode-1); p = repmat(v',1,maxStepsPerEpisode) - v; discountWeights = tril(discountFactor.^p);
Train the policy for the maximum number of episodes or until the average reward indicates that the policy is sufficiently trained.
for episodeCt = 1:numEpisodes episodeOffset = ... mod(episodeCt-1,trajectoriesForLearning)*maxStepsPerEpisode; % 1. Reset the environment at the start of the episode obs = reset(env); episodeReward = zeros(maxStepsPerEpisode,1); % 3. Generate experiences % for the maximum number of steps per episode % or until a terminal condition is reached. for stepCt = 1:maxStepsPerEpisode % Compute an action using the policy % based on the current observation. action = getAction(policy,{obs}); % Apply the action to the environment % and obtain the resulting observation and reward. [nextObs,reward,isdone] = step(env,action{1}); % Store the action, observation, % and reward experiences in their buffers. j = episodeOffset + stepCt; observationBuffer(:,:,j) = obs; actionBuffer(:,:,j) = action{1}; rewardBuffer(:,j) = reward; maskBuffer(:,j) = 1; obs = nextObs; % Stop if a terminal condition is reached. if isdone break; end end % Update the return buffer and the % cumulative reward for this episode. episodeElements = episodeOffset + (1:maxStepsPerEpisode); episodeCumulativeReward = extractdata( ... sum(rewardBuffer(episodeElements)) ); % 4. Compute the discounted future reward. returnBuffer(episodeElements) = ... rewardBuffer(episodeElements)*discountWeights; % Learn the set of aggregated trajectories. if mod(episodeCt,trajectoriesForLearning) == 0 % Get the indices of each action taken in the action buffer. actionIndicationMatrix = .... dlarray(single(actionBuffer(:,:) == actionSet)); % 5. Compute the gradient of the loss % with respect to the actor learnable parameters. actorGradient = dlfeval( ... actorGradFcn,... actor, ... {observationBuffer}, ... actionIndicationMatrix, ... returnBuffer, ... maskBuffer); % 6. Update the actor using the computed gradients. [actor,actorOptimizer] = update( ... actorOptimizer, ... actor, ... actorGradient); % Update the policy from the actor policy = rlStochasticActorPolicy(actor); % flush the mask and reward buffer maskBuffer(:) = 0; rewardBuffer(:) = 0; end % 7. Update the training visualization. episodeCumulativeRewardVector = cat(2,... episodeCumulativeRewardVector,episodeCumulativeReward); movingAvgReward = movmean(episodeCumulativeRewardVector,... avgWindowSize,2); addpoints(lineReward,episodeCt,episodeCumulativeReward); addpoints(lineAveReward,episodeCt,movingAvgReward(end)); drawnow; % 8. Terminate training if the network is sufficiently trained. if max(movingAvgReward) > trainingTerminationValue break end end
Simulation
Fix the random stream for reproducibility.
rng(0,"twister");After training, simulate the trained policy.
Before simulation, reset the environment and set the policy to use the maximum likelihood (greedy) action.
obs = reset(env); policy.UseMaxLikelihoodAction = true;
Enable the environment visualization, which is updated each time the environment step function is called.
plot(env)
For each simulation step, perform the following actions.
Get the action by sampling from the policy using the
getActionfunction.Step the environment using the obtained action value.
Terminate if a terminal condition is reached.
for stepCt = 1:maxStepsPerEpisode % Select action according to trained policy action = getAction(policy,{obs}); % Step the environment [nextObs,reward,isdone] = step(env,action{1}); % Check for terminal condition if isdone break end obs = nextObs; end

Restore the random number stream using the information stored in previousRngState.
rng(previousRngState);
Functions for Custom Training
To obtain actions and value functions for given observations from Reinforcement Learning Toolbox policy and value function approximators, you can use the following functions. These functions can also be used in automatically differentiated functions with dlfeval, dlgradient, and dlaccelerate.
getValue— Obtain the estimated state value or state-action value function.getAction— Obtain the action from an actor based on the current observation.getMaxQValue— Obtain the estimated maximum state-action value function for a discrete Q-value approximator.
If your policy or value function approximator is a recurrent neural network, that is, a neural network with at least one layer that has hidden state information, the preceding functions can return the current network state. You can use the following function syntaxes to get and set the state of your approximator.
state = critic.State— Obtain the state of approximatorcritic.critic.State = state— Set the state of approximator critic.
You can get and set the learnable parameters of your approximator using the getLearnableParameters and setLearnableParameters function, respectively.
In addition to these functions, you can use the dlgradient, update, and syncParameters functions to set parameters and compute gradients for your policy and value function approximators.
Loss Function
The loss function in the REINFORCE algorithm the product between the discounted reward and the logarithm of the probability distribution of the action (coming from the policy evaluation for a given observation), summed across all time steps. An additional entropy loss is added to improve exploration and reduce over-fitting during training.
function actorGradient = actorLossFunction( ... actor,observation,actionIndicationMatrix,discountedReturn,mask) % Compute the advantage and apply it % to the actions taken by the policy. advantage = actionIndicationMatrix.*discountedReturn.*mask; % Evaluate the action probabilities. % Set the UseForward name-value pair to true % to support cases where the actor has layers % that define a forward pass different than prediction % (e.g. batch normalization or dropout layers). out = evaluate(actor,observation,UseForward=true); actionProbabilities = out{1}; % Clip any action probability values less than eps to eps. actionProbabilities(actionProbabilities < eps) = eps; % Compute the log of the action probabilities. actionLogProbabilities = log(actionProbabilities); % Compute the policy gradient loss. pgLoss = -sum(advantage.*actionLogProbabilities,"all"); % Compute the entropy loss. entropyLoss = -sum( ... actionProbabilities.*actionLogProbabilities.*mask, ... "all"); % Compute the gradient of loss % with respect to the actor learnable parameters. loss = (pgLoss + 1e-4*entropyLoss)/(sum(mask)); actorGradient = dlgradient(loss,actor.Learnables); end
Helper Function
The following helper function creates a figure for training visualization.
function [trainingPlt, lineRewd, lineAvgRwd] = hBuildFigure() plotRatio = 16/9; trainingPlt = figure(... Visible="off",... HandleVisibility="off", ... NumberTitle="off",... Name="Cart Pole Custom Training"); trainingPlt.Position(3) = ... plotRatio * trainingPlt.Position(4); ax = gca(trainingPlt); lineRewd = animatedline(ax); lineAvgRwd = animatedline(ax,Color="r",LineWidth=3); xlabel(ax,"Episode"); ylabel(ax,"Reward"); legend(ax,"Cumulative Reward","Average Reward", ... Location="northwest") title(ax,"Training Progress"); end
See Also
Functions
dlaccelerate|dlgradient|dlfeval|evaluate|rlOptimizer|getLearnableParameters|setLearnableParameters