並列計算を使用した車線維持支援用 DQN エージェントの学習
この例では、並列学習を使用して、車線維持支援 (LKA) 用の深層 Q 学習ネットワーク (DQN) の学習を Simulink® で実行する方法を説明します。並列学習を使用しないでエージェントに学習させる方法を説明する例については、車線維持支援用 DQN エージェントの学習を参照してください。
DQN エージェントの詳細については、深層 Q ネットワーク (DQN) エージェントを参照してください。MATLAB® で DQN エージェントに学習させる例については、Train DQN Agent to Balance Discrete Cart-Pole Systemを参照してください。
DQN の並列学習の概要
DQN エージェントは経験ベースの並列化を使用しており、環境シミュレーションはワーカーによって実行され、勾配計算はクライアントによって実行されます。具体的には、各ワーカーはエージェントと環境のコピーから新しい経験を生成し、経験データをクライアントに送り返します。クライアント エージェントは次のようにパラメーターを更新します。
非同期学習の場合、クライアント エージェントは、すべてのワーカーから経験が送信されるのを待たずに、受信した経験から勾配を計算してエージェントのパラメーターを更新します。その後、クライアントは、経験を提供したワーカーに更新後のパラメーターを返信します。その後、ワーカーは、エージェントのコピーを更新し、環境のコピーを使用して経験の生成を続行します。非同期学習を指定するには、関数 train に渡す
rlTrainingOptionsオブジェクトのModeプロパティをasyncに設定しなければなりません。同期学習の場合、クライアント エージェントは、すべてのワーカーから経験が送信されるのを待ってから、それらすべての経験から勾配を計算します。クライアントは、エージェントのパラメーターを更新し、更新されたパラメーターをすべてのワーカーに同時に送信します。その後、すべてのワーカーは、エージェントの単一の更新済みコピー、および環境のコピーを使用して、経験を生成します。同期学習を指定するには、関数 train に渡す
rlTrainingOptionsオブジェクトのModeプロパティをsyncに設定しなければなりません。
経験ベースの並列化の詳細については、Train Agents Using Parallel Computing and GPUsを参照してください。
自車の Simulink モデル
この例では、自車の車両運動に関する単純な自転車モデルを強化学習の環境として使用します。学習の目標は、フロント ステアリング角度を調整することにより、車線のセンターラインに沿って自車を走行させ続けることです。この例では、車線維持支援用 DQN エージェントの学習と同じ車両モデルを使用します。
m = 1575; % total vehicle mass (kg) Iz = 2875; % yaw moment of inertia (mNs^2) lf = 1.2; % longitudinal distance from CG to front tires (m) lr = 1.6; % longitudinal distance from CG to rear tires (m) Cf = 19000; % cornering stiffness of front tires (N/rad) Cr = 33000; % cornering stiffness of rear tires (N/rad) Vx = 15; % longitudinal velocity (m/s)
サンプル時間 Ts とシミュレーション期間 T を秒単位で定義します。
Ts = 0.1; T = 15;
LKA システムの出力は、自車のフロント ステアリング角度です。自車の物理的なステアリング範囲をシミュレートするために、ステアリング角度を [–0.5,0.5] rad の範囲に制限します。
u_min = -0.5; u_max = 0.5;
道路の曲率は定数 0.001 () で定義されます。横方向の偏差の初期値は 0.2 m、相対ヨー角の初期値は –0.1 rad です。
rho = 0.001; e1_initial = 0.2; e2_initial = -0.1;
モデルを開きます。
mdl = "rlLKAMdl"; open_system(mdl) agentblk = mdl + "/RL Agent";
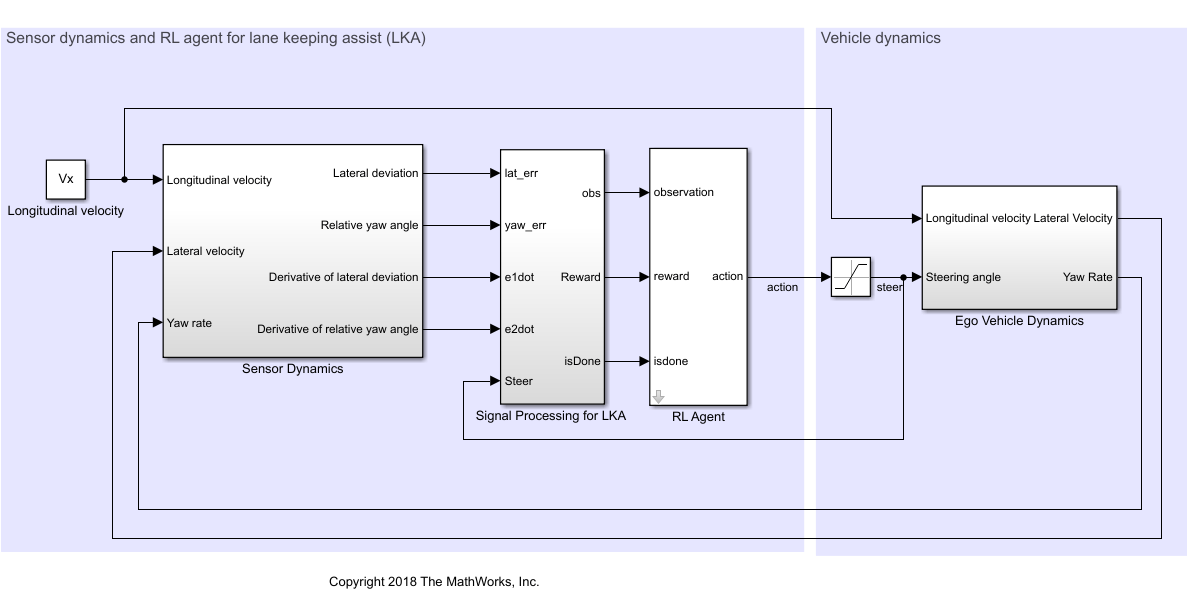
このモデルでは、次のようにします。
エージェントから環境へのステアリング角度アクション信号は、-15 ~ 15 度とする。
環境からの観測値は、横方向の偏差 、相対ヨー角 、これらの微分 および 、これらの積分 および とする。
シミュレーションは、横方向の偏差が となったときに終了する。
各タイム ステップ で与えられる報酬 は次のとおりとする。
ここで、 は前のタイム ステップ からの制御入力です。
環境インターフェイスの作成
自車用の強化学習環境オブジェクトを作成します。
観測の情報を定義します。
obsInfo = rlNumericSpec([6 1], ... LowerLimit=-inf*ones(6,1), ... UpperLimit=inf*ones(6,1)); obsInfo.Name = "observations"; obsInfo.Description = ... "lateral deviation and relative yaw angle";
アクションの情報を定義します。
actInfo = rlFiniteSetSpec((-15:15)*pi/180);
actInfo.Name = "steering";環境オブジェクトを作成します。
env = rlSimulinkEnv(mdl,agentblk,obsInfo,actInfo);
オブジェクトは離散行動空間をもち、エージェントは -15 度 ~ 15 度の 31 種類の可能なステアリング角のいずれかを適用できます。観測値は、横方向の偏差、相対ヨー角、これらの時間微分、これらの時間積分から成る 6 次元のベクトルです。
横方向の偏差と相対ヨー角の初期条件を定義するために、無名関数ハンドルを使用して環境のリセット関数 localResetFcn を指定します。これは、この例の最後で定義されており、横方向の偏差と相対ヨー角の初期値をランダム化します。
env.ResetFcn = @(in)localResetFcn(in);
DQN エージェントの作成
DQN エージェントは、パラメーター化された Q 値関数近似器を使用して方策の価値を推定します。DQN エージェントは離散行動空間をもちますが、(多出力の) ベクトル Q 値関数クリティックを作成することもできます。これは通常、単出力クリティックよりも効率的です。
ベクトル Q 値関数は、観測値のみを入力として取り、可能なアクションと同じ数の要素をもつ単一のベクトルを出力として返します。各出力要素の値は、エージェントが与えられた観測値に対応する状態から開始し、要素の数に対応するアクションを実行する (その後は与えられた方策に従う) ときの、期待される割引累積長期報酬を表します。
パラメーター化された Q 値関数をクリティック内でモデル化するには、1 つの入力 (観測された 6 次元の状態) と 31 個の要素から成る 1 つの出力ベクトル (-15 度~ 15 度の範囲で等間隔に配置されたステアリング角度) をもつニューラル ネットワークを使用します。環境仕様から、観測空間の次元の数および離散行動空間の要素の数を取得します。
nI = obsInfo.Dimension(1); % number of inputs (6) nL = 120; % number of neurons nO = numel(actInfo.Elements); % number of outputs (31)
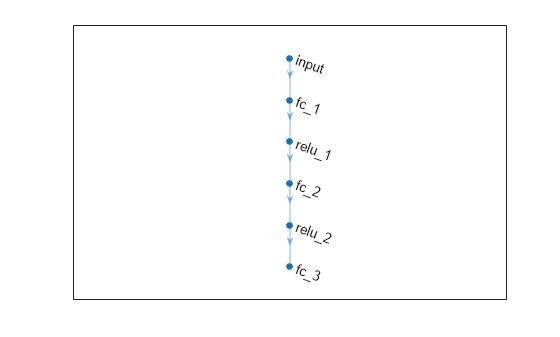
ネットワークを layer オブジェクトの配列として定義します。
dnn = [
featureInputLayer(nI)
fullyConnectedLayer(nL)
reluLayer
fullyConnectedLayer(nL)
reluLayer
fullyConnectedLayer(nO)
];クリティック ネットワークはランダムに初期化されます。乱数発生器のシード値を固定して、セクションの再現性を確保します。
rng(0)
dlnetwork オブジェクトに変換し、パラメーターの数を表示します。
dnn = dlnetwork(dnn); summary(dnn)
Initialized: true
Number of learnables: 19.1k
Inputs:
1 'input' 6 features
ネットワーク構成を表示します。
plot(dnn)
dnn と環境仕様を使用して、クリティックを作成します。ベクトル Q 値関数近似器の詳細については、rlVectorQValueFunctionを参照してください。
critic = rlVectorQValueFunction(dnn,obsInfo,actInfo);
rlOptimizerOptionsを使用して、クリティックの学習オプションを指定します。
criticOptions = rlOptimizerOptions( ... LearnRate=1e-4, ... GradientThreshold=1, ... L2RegularizationFactor=1e-4);
rlDQNAgentOptionsを使用して、DQN エージェントのオプション (クリティックのオプションのオブジェクトなど) を指定します。
agentOpts = rlDQNAgentOptions(... SampleTime=Ts,... UseDoubleDQN=true,... CriticOptimizerOptions=criticOptions,... ExperienceBufferLength=1e6,... MiniBatchSize=256);
ドット表記を使用してエージェントのオプションを設定または変更することもできます。
agentOpts.EpsilonGreedyExploration.EpsilonDecay = 1e-4;
または、最初にエージェントを作成してから、ドット表記を使用してそのオプション オブジェクトにアクセスしてオプションを変更することもできます。
指定したクリティックとエージェントのオプションを使用して、DQN エージェントを作成します。詳細については、rlDQNAgentを参照してください。
agent = rlDQNAgent(critic,agentOpts);
学習オプション
エージェントに学習させるには、まず、学習オプションを指定します。この例では、次のオプションを使用します。
最大 10000 個のエピソードについて、各学習を実行 (各エピソードの持続時間は最大
ceil(T/Ts)タイム ステップ)。Episode Manager のダイアログ ボックスにのみ学習の進行状況を表示 (
PlotsオプションとVerboseオプションをそれぞれ設定)。エピソード報酬が -1 に達したときに学習を停止。
累積報酬が 100 を超える各エピソードについてエージェントのコピーを保存。
学習オプションの詳細については、rlTrainingOptionsを参照してください。
maxepisodes = 10000; maxsteps = ceil(T/Ts); trainOpts = rlTrainingOptions(... MaxEpisodes=maxepisodes, ... MaxStepsPerEpisode=maxsteps, ... Verbose=false,... Plots="training-progress",... StopTrainingCriteria="EpisodeReward",... StopTrainingValue= -1,... SaveAgentCriteria="EpisodeReward",... SaveAgentValue=100);
並列学習のオプション
並列でエージェントに学習させるには、次の学習オプションを指定します。
UseParallelオプションをtrueに設定。ParallelizationOptions.Modeオプションを"async"に設定し、エージェントの学習を並列で非同期に実行。
trainOpts.UseParallel = true;
trainOpts.ParallelizationOptions.Mode = "async";学習オプションの詳細については、rlTrainingOptionsを参照してください。
エージェントの学習
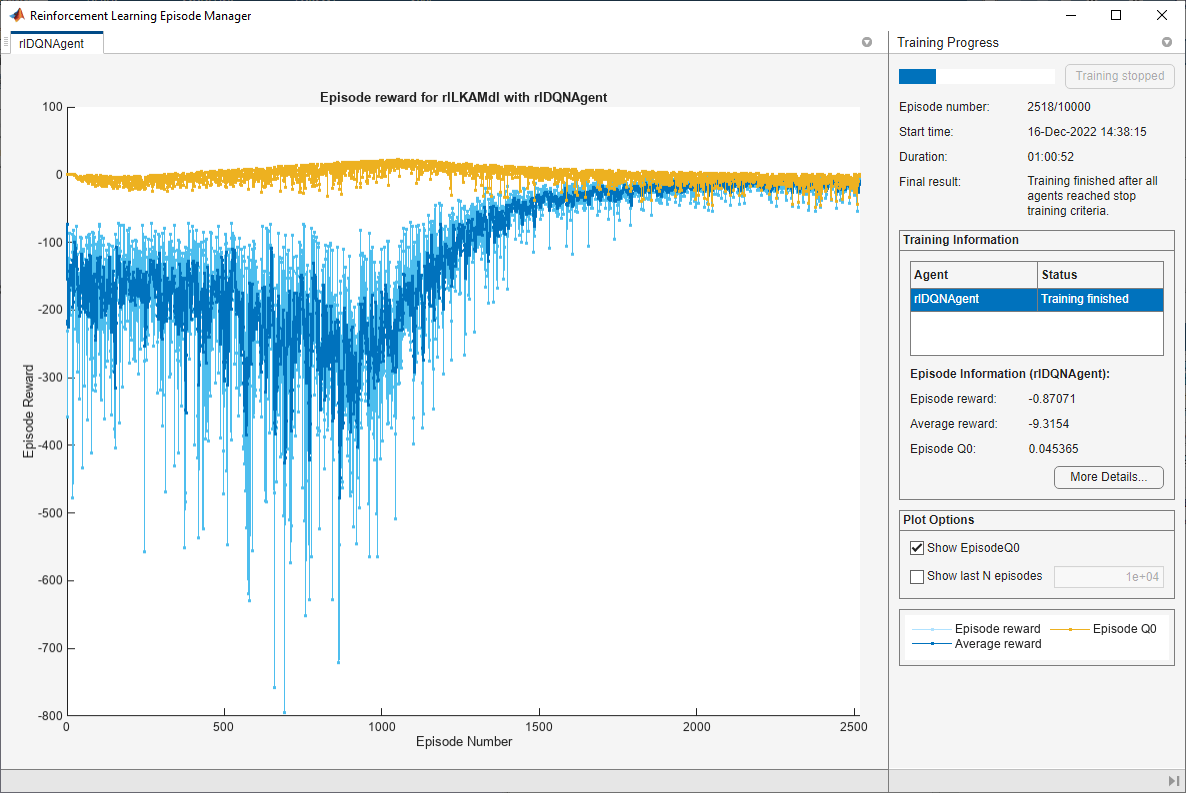
関数 train を使用して、エージェントに学習させます。エージェントの学習は計算量が多いプロセスのため、完了するのに数分かかります。この例の実行時間を節約するために、doTraining を false に設定して事前学習済みのエージェントを読み込みます。エージェントに学習させるには、doTraining を true に設定します。並列学習にはランダム性が存在するため、通常、次のプロットとは異なる学習結果が得られます。このプロットは、4 つのワーカーを使用して学習させた結果を示しています。
doTraining = false; if doTraining % Train the agent. trainingStats = train(agent,env,trainOpts); else % Load pretrained agent for the example. load("SimulinkLKADQNParallel.mat","agent") end
エージェントのシミュレーション
学習済みエージェントの性能を検証するには、次の 2 つの行のコメントを解除し、環境内でこのエージェントをシミュレートします。エージェントのシミュレーションの詳細については、rlSimulationOptions および sim を参照してください。
% simOptions = rlSimulationOptions(MaxSteps=maxsteps); % experience = sim(env,agent,simOptions);
確定的な初期条件を使用して学習済みエージェントのデモを実行するには、このモデルを Simulink でシミュレートします。
e1_initial = -0.4; e2_initial = 0.2; sim(mdl)
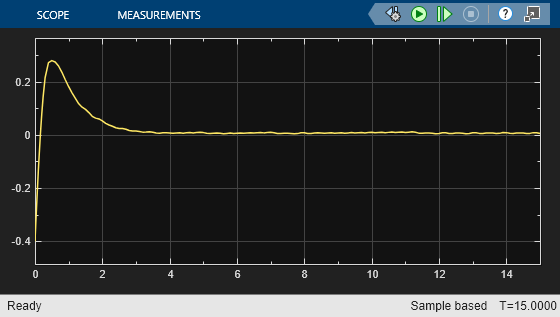
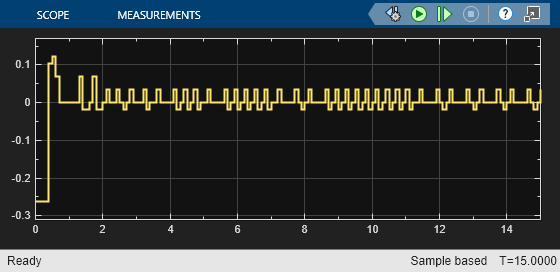
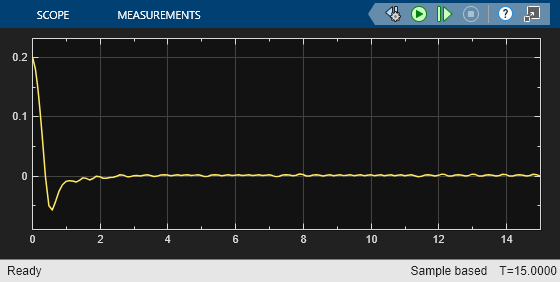
これらのプロットが示すように、横方向の誤差 (上部プロット) と相対ヨー角 (下部プロット) は両方とも 0 に近づきます。車両はセンターラインから外れた位置 (-0.4 m)、およびヨー角の誤差が 0 でない状態 (0.2 rad) から出発します。LKA によって、2.5 秒後に自車がセンターラインに沿って走行するようになります。ステアリング角 (中央プロット) は、コントローラーが 2 秒後に定常状態に達することを示しています。
ローカル関数
function in = localResetFcn(in) % set initial lateral deviation and relative yaw angle to random values in = setVariable(in,"e1_initial", 0.5*(-1+2*rand)); in = setVariable(in,"e2_initial", 0.1*(-1+2*rand)); end
参考
関数
train|sim|rlSimulinkEnv
オブジェクト
ブロック
トピック
- 車線維持支援用 DQN エージェントの学習
- Train PPO Agent with Curriculum Learning for a Lane Keeping Application
- Lane Keeping Assist with Lane Detection (Automated Driving Toolbox)
- Lane Keeping Assist System Using Model Predictive Control (Model Predictive Control Toolbox)
- Train AC Agent to Balance Discrete Cart-Pole System Using Parallel Computing
- 強化学習エージェントを使用した二足歩行ロボットの学習
- Create Policies and Value Functions
- 深層 Q ネットワーク (DQN) エージェント
- Train Reinforcement Learning Agents
- Train Agents Using Parallel Computing and GPUs