Train DDPG Agent to Swing Up and Balance Pendulum with Bus Signal
This example shows how to convert a simple frictionless pendulum Simulink® model to a reinforcement learning environment object, and how to train a deep deterministic policy gradient (DDPG) agent in this environment.
For more information on DDPG agents, see Deep Deterministic Policy Gradient (DDPG) Agent. For an example showing how to train a DDPG agent in MATLAB®, see Compare DDPG Agent to LQR Controller.
Pendulum Swing-Up Model with Bus
The starting model for this example is a simple frictionless pendulum. The training goal is to make the pendulum stand upright using minimal control effort.
Open the model.
mdl = "rlSimplePendulumModelBus";
open_system(mdl)
In this model:
The balanced, upright pendulum position is zero radians, and the downward hanging pendulum position is
piradians.The torque action signal from the agent to the environment is from –2 to 2 N·m.
The observations from the environment are the sine of the pendulum angle, the cosine of the pendulum angle, and the pendulum angle derivative.
Both the observation and action signals are Simulink buses.
The reward , provided at every time step, is
.
Here:
is the angle of displacement from the upright position.
is the derivative of the displacement angle.
is the control effort from the previous time step.
The model used in this example is similar to the simple pendulum model described in Load Predefined Control System Environments. The difference is that the model in this example uses Simulink buses for the action and observation signals.
Create Environment Interface with Bus
The environment object from a Simulink model is created using rlSimulinkEnv, which requires the name of the Simulink model, the path to the agent block, and observation and action reinforcement learning data specifications. For models that use bus signals for actions or observations, you can create the corresponding specifications using the bus2RLSpec function.
Specify the path to the agent block.
agentBlk = "rlSimplePendulumModelBus/RL Agent";Create the observation Bus object. The channel names must correspond to the signal names specified in the Simulink buses used to create the observation and action signals.
obsBus = Simulink.Bus(); obs(1) = Simulink.BusElement; obs(1).Name = "sin_theta"; obs(2) = Simulink.BusElement; obs(2).Name = "cos_theta"; obs(3) = Simulink.BusElement; obs(3).Name = "dtheta"; obsBus.Elements = obs;
Create the action Bus object.
actBus = Simulink.Bus();
act(1) = Simulink.BusElement;
act(1).Name = "tau";
act(1).Min = -2;
act(1).Max = 2;
actBus.Elements = act;Create the action and observation specification objects using the Simulink buses.
obsInfo = bus2RLSpec("obsBus","Model",mdl)
obsInfo=1×3 rlNumericSpec array with properties:
LowerLimit
UpperLimit
Name
Description
Dimension
DataType
actInfo = bus2RLSpec("actBus","Model",mdl)
actInfo =
rlNumericSpec with properties:
LowerLimit: -2
UpperLimit: 2
Name: "tau"
Description: ""
Dimension: [1 1]
DataType: "double"
Create the reinforcement learning environment for the pendulum model.
env = rlSimulinkEnv(mdl,agentBlk,obsInfo,actInfo);
To define the initial condition of the pendulum as hanging downward, specify an environment reset function using an anonymous function handle. This reset function sets the model workspace variable theta0 to pi.
env.ResetFcn = @(in)setVariable(in,"theta0",pi,"Workspace",mdl);
Specify the agent sample time Ts and the simulation time Tf in seconds.
Ts = 0.05; Tf = 20;
Fix the random generator seed for reproducibility.
rng(0)
Create DDPG Agent
DDPG agents use a parametrized deterministic policy over continuous action spaces, which is learned by a continuous deterministic actor. This actor takes the current observation as input and returns as output an action that is a deterministic function of the observation.
To model the parametrized policy within the actor, use a neural network with three input layers (each receiving one scalar observation, as specified by obsInfo) and one output layer (which returns the action to the environment action channel, as specified by actInfo).
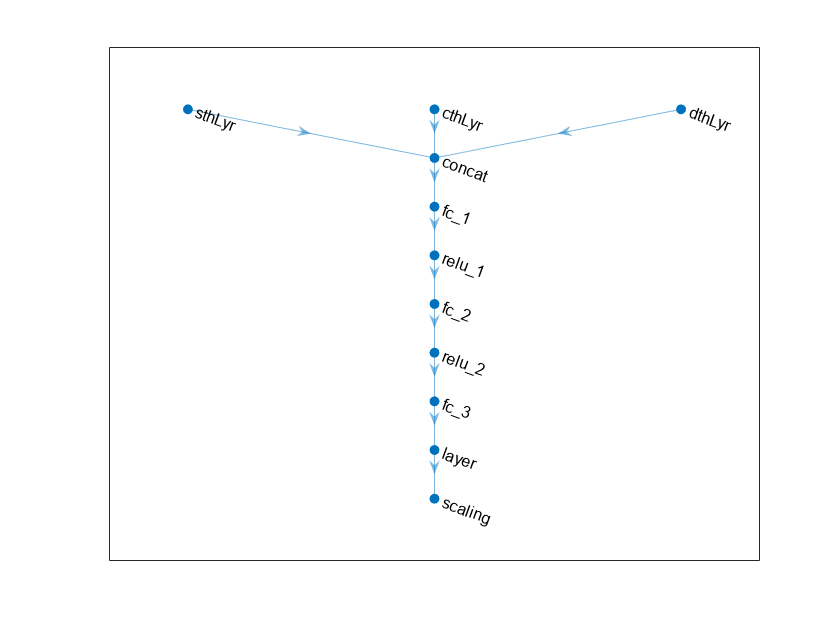
Define the network as an array of layer objects, and combine the outputs from the input layers using a concatenationLayer. Since the output of tanhLayer is limited between -1 and 1, scale the network output to the range of the action using scalingLayer.
For more information on creating actors based on deep neural networks, see Create Policies and Value Functions.
% Define input layers. sinThetaInputLayer = featureInputLayer(1,Name="sthLyr"); cosThetaInputLayer = featureInputLayer(1,Name="cthLyr"); dThetaInputLayer = featureInputLayer(1,Name="dthLyr"); % Define common path. commonPath = [ concatenationLayer(1,3,Name="concat") fullyConnectedLayer(400) reluLayer fullyConnectedLayer(300) reluLayer fullyConnectedLayer(1) tanhLayer scalingLayer(Scale=max(actInfo.UpperLimit)) ];
Create dlnetwork object and add layers.
actorNetwork = dlnetwork; actorNetwork = addLayers(actorNetwork,sinThetaInputLayer); actorNetwork = addLayers(actorNetwork,cosThetaInputLayer); actorNetwork = addLayers(actorNetwork,dThetaInputLayer); actorNetwork = addLayers(actorNetwork,commonPath);
Connect layers.
actorNetwork = connectLayers(actorNetwork,"sthLyr","concat/in1"); actorNetwork = connectLayers(actorNetwork,"cthLyr","concat/in2"); actorNetwork = connectLayers(actorNetwork,"dthLyr","concat/in3");
Initialize network and display the number of weights.
actorNetwork = initialize(actorNetwork); summary(actorNetwork)
Initialized: true
Number of learnables: 122.2k
Inputs:
1 'sthLyr' 1 features
2 'cthLyr' 1 features
3 'dthLyr' 1 features
View the actor network configuration.
plot(actorNetwork)
Create the actor using the specified deep neural network. Specify the action and observation info for the actor, as well as the names of the network input layers to be connected with the observation channels. For more information, see rlContinuousDeterministicActor.
actor = rlContinuousDeterministicActor(actorNetwork,obsInfo,actInfo,... "ObservationInputNames",["sthLyr","cthLyr","dthLyr"]);
DDPG agents use a parametrized Q-value function approximator to estimate the value of the policy. A Q-value function critic takes the current observation and an action as inputs and returns a single scalar as output (the estimated discounted cumulative long-term reward for which receives the action from the state corresponding to the current observation, and following the policy thereafter).
To model the parametrized Q-value function within the critic, use a neural network with four input layers (three for the observation channels, as specified by obsInfo, and the other for the action channel, as specified by actInfo) and one output layer (which returns the scalar value).
Define each network path as an array of layer objects, assigning names to the input and output layers of each path. Use the input layers previously defined for the actor.
% Define observation path. obsPath = [ concatenationLayer(1,3,Name="concat") fullyConnectedLayer(400) reluLayer fullyConnectedLayer(300,Name="obsPathOutLyr") ]; % Define action path. actPath = [ featureInputLayer(1,Name= "action") fullyConnectedLayer(300, ... Name="actPathOutLyr", ... BiasLearnRateFactor=0) ]; % Define common path. commonPath = [ additionLayer(2,Name="add") reluLayer fullyConnectedLayer(1,Name="CriticOutput") ];
Create dlnetwork object and add layers.
criticNetwork = dlnetwork; criticNetwork = addLayers(criticNetwork,sinThetaInputLayer); criticNetwork = addLayers(criticNetwork,cosThetaInputLayer); criticNetwork = addLayers(criticNetwork,dThetaInputLayer); criticNetwork = addLayers(criticNetwork,actPath); criticNetwork = addLayers(criticNetwork,obsPath); criticNetwork = addLayers(criticNetwork,commonPath);
Connect layers.
criticNetwork = connectLayers(criticNetwork,"sthLyr","concat/in1"); criticNetwork = connectLayers(criticNetwork,"cthLyr","concat/in2"); criticNetwork = connectLayers(criticNetwork,"dthLyr","concat/in3"); criticNetwork = connectLayers(criticNetwork,"obsPathOutLyr","add/in1"); criticNetwork = connectLayers(criticNetwork,"actPathOutLyr","add/in2");
Initialize network and display the number of weights.
criticNetwork = initialize(criticNetwork); summary(criticNetwork)
Initialized: true
Number of learnables: 122.8k
Inputs:
1 'sthLyr' 1 features
2 'cthLyr' 1 features
3 'dthLyr' 1 features
4 'action' 1 features
Create the critic approximator object using criticNet, the environment observation and action specifications, and the names of the network input layers to be connected with the environment observation and action channels. For more information, see rlQValueFunction.
critic = rlQValueFunction(criticNetwork, ... obsInfo,actInfo,... ObservationInputNames=["sthLyr","cthLyr","dthLyr"], ... ActionInputNames="action");
Specify options for the critic and actor using rlOptimizerOptions.
criticOptions = rlOptimizerOptions(LearnRate=1e-03,GradientThreshold=1); actorOptions = rlOptimizerOptions(LearnRate=1e-03,GradientThreshold=1);
To create the DDPG agent, first specify the DDPG agent options using rlDDPGAgentOptions.
agentOpts = rlDDPGAgentOptions(... SampleTime=Ts,... CriticOptimizerOptions=criticOptions,... ActorOptimizerOptions=actorOptions,... ExperienceBufferLength=1e5,... DiscountFactor=0.99,... MiniBatchSize=128); agentOpts.NoiseOptions.StandardDeviation = 0.6;
Then create the DDPG agent using the specified actor representation, critic representation, and agent options. For more information, see rlDDPGAgent.
agent = rlDDPGAgent(actor,critic,agentOpts);
Train Agent
To train the agent, first specify the training options. For this example, use the following options:
Run each training for a maximum of 50,000 episodes, with each episode lasting at most
ceil(Tf/Ts)time steps.Display the training progress in the Reinforcement Learning Training Monitor dialog box (set the
Plotsoption) and disable the command line display (set theVerboseoption tofalse).Stop training when the agent receives an average cumulative reward greater than –740 when evaluating the deterministic policy. At this point, the agent can quickly balance the pendulum in the upright position using minimal control effort.
Save a copy of the agent for each episode where the cumulative reward is greater than –740.
For more information on training options, see rlTrainingOptions.
maxepisodes = 5000; maxsteps = ceil(Tf/Ts); trainOpts = rlTrainingOptions(... MaxEpisodes=maxepisodes,... MaxStepsPerEpisode=maxsteps,... ScoreAveragingWindowLength=5,... Verbose=false,... Plots="training-progress",... StopTrainingCriteria="EvaluationStatistic",... StopTrainingValue=-740);
Train the agent using the train function. Training this agent is a computationally intensive process that takes several hours to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.
doTraining = false; if doTraining % Use the rlEvaluator object to measure policy performance every 10 % episodes evaluator = rlEvaluator(... NumEpisodes=1,... EvaluationFrequency=10); % Train the agent. trainingStats = train(agent,env,trainOpts,Evaluator=evaluator); else % Load the pretrained agent for the example. load("SimulinkPendBusDDPG.mat","agent") end

Simulate DDPG Agent
To validate the performance of the trained agent, simulate it within the pendulum environment. For more information on agent simulation, see rlSimulationOptions and sim.
simOptions = rlSimulationOptions(MaxSteps=500); experience = sim(env,agent,simOptions);
See Also
Functions
rlSimulinkEnv|bus2RLSpec|train|sim
Objects
rlDDPGAgent|rlDDPGAgentOptions|rlQValueFunction|rlContinuousDeterministicActor|rlTrainingOptions|rlSimulationOptions|rlOptimizerOptions