fminimax

ミニマックス制約付き問題を解く

構文

x = fminimax(fun,x0)

x = fminimax(fun,x0,A,b)

x = fminimax(fun,x0,A,b,Aeq,beq)

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

x = fminimax(problem)

[x,fval] = fminimax(___)

[x,fval,maxfval,exitflag,output] = fminimax(___)

[x,fval,maxfval,exitflag,output,lambda] = fminimax(___)

説明

fminimax は、一連の目的関数の最大値を最小化する点を探します。

この問題には任意のタイプの制約が含まれます。具体的には、fminimax は、以下で指定される問題の最小値を求めます。

$$\underset{x}{\min }\underset{i}{\max }{F}_i(x)\text{ such that }\{\begin{array}{c}c(x)\le 0\\ ceq(x)=0\\ A\cdot x\le b\\ Aeq\cdot x=beq\\ lb\le x\le ub\end{array}$$

ここで、b と beq はベクトル、A と Aeq は行列、c(x)、ceq(x)、F(x) はベクトルを返す関数です。F(x)、c(x)、ceq(x) を非線形関数にすることもできます。

x、lb および ub はベクトルまたは行列として渡すことができます。行列引数を参照してください。

また、単位行列を使用して、fminimax で最大最小の問題を解くこともできます。

$$\underset{x}{\max }\underset{i}{\min }{F}_i(x)=-\underset{x}{\min }\underset{i}{\max }\left(-F_i(x)\right).$$

以下の形式の問題を解くことができます。

$$\underset{x}{\min }\underset{i}{\max }\left|F_i(x)\right|$$

この問題を解くには AbsoluteMaxObjectiveCount オプションを使用します。1 つの目的関数の絶対値を使用したミニマックス問題の解法を参照してください。

x = fminimax(fun,x0) は、x0 を開始値として fun に記述する関数のミニマックス解 x を求めます。

メモ

追加パラメーターの受け渡し は、必要に応じて他のパラメーターを目的関数と非線形制約関数に渡す方法を説明します。

x = fminimax(fun,x0,A,b) は線形不等式 A*x ≤ b を制約とするミニマックス問題を解きます。

x = fminimax(fun,x0,A,b,Aeq,beq) は同様に、線形等式 Aeq*x = beq を制約とするミニマックス問題を解きます。不等式が存在しない場合は A = [] および b = [] と設定してください。

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub) は範囲 lb ≤ x ≤ ub を制約とするミニマックス問題を解きます。等式が存在しない場合には Aeq = [] と beq = [] を設定してください。x(i) が下に非有界の場合は lb(i) = –Inf を設定してください。x(i) が上に非有界の場合は ub(i) = Inf を設定してください。

メモ

反復は制約に違反する可能性ありを参照してください。

メモ

問題の指定された入力範囲が矛盾する場合、出力 x は x0、出力 fval は [] です。

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) は、非線形不等式 c(x) または nonlcon に定義する等式 ceq(x) を制約とするミニマックス問題を解きます。この関数は c(x) ≤ 0 および ceq(x) = 0 の下で最適化を行います。範囲が存在しない場合は、lb = [] または ub = []、あるいはその両方を設定します。

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) は、options で指定された最適化オプションを使ってミニマックス問題を解きます。optimoptions を使用してこれらのオプションを設定してください。

x = fminimax(problem) は、problemで説明されている構造体 problem に関するミニマックス問題を解きます。

[x,fval] = fminimax(___) は、どの構文でも、解 x での fun で計算された目的関数の値を返します。

[x,fval,maxfval,exitflag,output] = fminimax(___) は上記に加え、解 x における目的関数の最大値、fminimax の終了条件を記述する値 exitflag、および最適化プロセスに関する情報を含む構造体 output を返します。

[x,fval,maxfval,exitflag,output,lambda] = fminimax(___) は上記に加え、解 x におけるラグランジュ乗数をフィールドに含む、構造体 lambda を返します。

例

sin と cos の最大値の最小化

関数 sin および cos と、区間 [–pi,pi] でのこれらの関数の最大値のプロットを作成します。

t = linspace(-pi,pi);
plot(t,sin(t),'r-')
hold on
plot(t,cos(t),'b-');
plot(t,max(sin(t),cos(t)),'ko')
legend('sin(t)','cos(t)','max(sin(t),cos(t))','Location','NorthWest')

このプロットは、最大値の 2 つの局所的最小値 (1 に近い値と –2 に近い値) を示しています。1 に近い最小値を求めます。

fun = @(x)[sin(x);cos(x)];
x0 = 1;
x1 = fminimax(fun,x0)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x1 = 
0.7854

–2 に近い最小値を求めます。

x0 = -2;
x2 = fminimax(fun,x0)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x2 = 
-2.3562

線形制約付きミニマックス問題の解法

この例の目的関数は、線形であり定数です。目的関数の詳細とプロットについては、fminimax と fminunc の比較を参照してください。

3 つのベクトル $$v$$ および 3 つの定数 $$v_0$$ について、$$dot(x,v)+v_0$$ の形式の 3 つの線形関数として目的関数を設定します。

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

不等式 x(1) + 3*x(2) <= –4 を制約とするミニマックス点を求めます。

A = [1,3];
b = -4;
x0 = [-1,-2];
x = fminimax(fun,x0,A,b)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x = 1×2

   -5.8000    0.6000

範囲制約付きミニマックス問題の解法

この例の目的関数は、線形であり定数です。目的関数の詳細とプロットについては、fminimax と fminunc の比較を参照してください。

3 つのベクトル $$v$$ および 3 つの定数 $$v_0$$ について、$$dot(x,v)+v_0$$ の形式の 3 つの線形関数として目的関数を設定します。

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

範囲 –2 <= x(1) <= 2 および –1 <= x(2) <= 1 を設定し、[0,0] から始めてミニマックス問題を解きます。

lb = [-2,-1];
ub = [2,1];
x0 = [0,0];
A = []; % No linear constraints
b = [];
Aeq = [];
beq = [];
[x,fval] = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x = 1×2

   -0.0000    1.0000

fval = 1×3

    3.0000   -2.0000    3.0000

この場合、解は一意ではありません。多くの点が制約を満たし、ミニマックス値が同じになります。3 つの目的関数の最大値を表す表面をプロットし、ミニマックス値が同じになる点を示す赤い線をプロットします。

[X,Y] = meshgrid(linspace(-2,2),linspace(-1,1));
Z = max(fun([X(:),Y(:)]),[],2);
Z = reshape(Z,size(X));
surf(X,Y,Z,'LineStyle','none')
view(-118,28)
hold on
line([-2,0],[1,1],[3,3],'Color','r','LineWidth',8)
hold off

非線形制約の下でミニマックスを求める

この例の目的関数は、線形であり定数です。目的関数の詳細とプロットについては、fminimax と fminunc の比較を参照してください。

3 つのベクトル $$v$$ および 3 つの定数 $$v_0$$ について、$$dot(x,v)+v_0$$ の形式の 3 つの線形関数として目的関数を設定します。

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

関数 unitdisk は、非線形不等式制約 $$\Vert x{\Vert }^2\le 1$$ を表します。

type unitdisk

function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];

x0 = [0,0] から開始して、unitdisk を制約とするミニマックス問題を解きます。

x0 = [0,0];
A = []; % No other constraints
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = @unitdisk;
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x = 1×2

   -0.0000    1.0000

1 つの目的関数の絶対値を使用したミニマックス問題の解法

fminimax は、AbsoluteMaxObjectiveCount オプションを使用して、$$i$$ の最初のいくつかの値について $$F_i(x)$$ または $$|F_i(x)|$$ のいずれかの最大値を最小化できます。$$k$$ 個の目的関数の絶対値を最小化するには、$$F_1(x)$$ から $$F_k(x)$$ が絶対値の最小化の目的関数となるように目的関数値を配置し、AbsoluteMaxObjectiveCount オプションを k に設定します。

この例では、sin と cos の最大値を最小化し、sin を最初の目的関数に指定し、AbsoluteMaxObjectiveCount を 1 に設定します。

fun = @(x)[sin(x),cos(x)];
options = optimoptions('fminimax','AbsoluteMaxObjectiveCount',1);
x0 = 1;
A = []; % No constraints
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x1 = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x1 = 
0.7854

まず x0 = –2 から試します。

x0 = -2;
x2 = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x2 = 
-3.1416

関数をプロットします。

t = linspace(-pi,pi);
plot(t,max(abs(sin(t)),cos(t)))

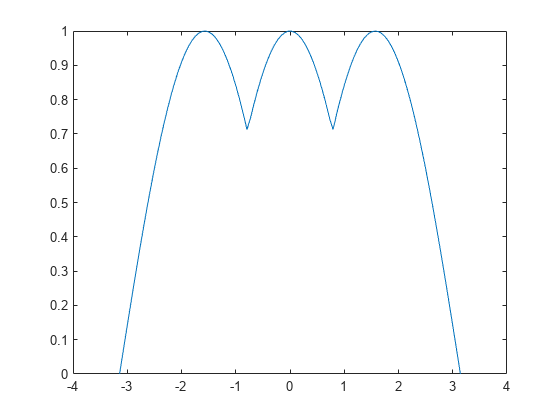
AbsoluteMaxObjectiveCount オプションの効果を確認するには、このプロットとsin と cos の最大値の最小化の例のプロットを比較します。

ミニマックス値の取得

ミニマックス点の位置と目的関数の値の両方を取得します。目的関数の詳細とプロットについては、fminimax と fminunc の比較を参照してください。

3 つのベクトル $$v$$ および 3 つの定数 $$v_0$$ について、$$dot(x,v)+v_0$$ の形式の 3 つの線形関数として目的関数を設定します。

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

初期点を [0,0] に設定し、ミニマックス点とミニマックス値を求めます。

x0 = [0,0];
[x,fval] = fminimax(fun,x0)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x = 1×2

   -2.5000    2.2500

fval = 1×3

    1.7500    1.7500    1.7500

3 つすべての目的関数のミニマックス点での値が同じになります。制約なしの問題には、一般的に、解において等しくなる目的関数が少なくとも 2 つあります。これは、点が任意の目的関数の局所的最小値ではなく、1 つの目的関数にのみ最大値がある場合、目的関数の最大値をより小さくできるためです。

すべてのミニマックス出力の取得

この例の目的関数は、線形であり定数です。目的関数の詳細とプロットについては、fminimax と fminunc の比較を参照してください。

3 つのベクトル $$v$$ および 3 つの定数 $$v_0$$ について、$$dot(x,v)+v_0$$ の形式の 3 つの線形関数として目的関数を設定します。

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

不等式 x(1) + 3*x(2) <= –4 を制約とするミニマックス点を求めます。

A = [1,3];
b = -4;
x0 = [-1,-2];

反復表示のオプションを設定し、すべてのソルバー出力を取得します。

options = optimoptions('fminimax','Display','iter');
Aeq = []; % No other constraints
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval,maxfval,exitflag,output,lambda] =...
    fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

                  Objective        Max     Line search     Directional 
 Iter F-count         value    constraint   steplength      derivative   Procedure 
    0      4              0             6                                            
    1      9              5             0            1           0.981     
    2     14          4.889     8.882e-16            1          -0.302    Hessian modified twice  
    3     19            3.4     8.132e-09            1          -0.302    Hessian modified twice  

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

<stopping criteria details>

x = 1×2

   -5.8000    0.6000

fval = 1×3

   -3.2000    3.4000    3.4000

maxfval = 
3.4000

exitflag = 
4

output = struct with fields:
         iterations: 4
          funcCount: 19
       lssteplength: 1
           stepsize: 6.0684e-10
          algorithm: 'active-set'
      firstorderopt: []
    constrviolation: 8.1323e-09
            message: 'Local minimum possible. Constraints satisfied.↵↵fminimax stopped because the size of the current search direction is less than↵twice the value of the step size tolerance and constraints are ↵satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization stopped because the norm of the current search direction, 4.555377e-10,↵is less than 2*options.StepTolerance = 1.000000e-06, and the maximum constraint ↵violation, 8.132313e-09, is less than options.ConstraintTolerance = 1.000000e-06.'

lambda = struct with fields:
         lower: [2×1 double]
         upper: [2×1 double]
         eqlin: [0×1 double]
      eqnonlin: [0×1 double]
       ineqlin: 0.2000
    ineqnonlin: [0×1 double]

返される情報を確認します。

• 解において 2 つの目的関数値が等しくなっています。

• ソルバーが 4 回の反復と 19 回の関数評価で収束しています。

• lambda.ineqlin の値が非ゼロです。これは、線形制約が解においてアクティブであることを示します。

入力引数

fun — 目的関数

関数ハンドル | 関数名

目的関数。関数ハンドルまたは関数名として指定します。fun は、ベクトル x を受け入れ、ベクトル F (x で評価される目的関数) を返す関数です。関数 fun は関数ファイルの関数ハンドルとして指定することができます。

x = fminimax(@myfun,x0,goal,weight)

ここで myfun は次のような MATLAB^® 関数です。

function F = myfun(x)
F = ...         % Compute function values at x.

fun は無名関数の関数ハンドルにもなります。

x = fminimax(@(x)sin(x.*x),x0,goal,weight);

fminimax は、目的関数および任意の非線形制約関数に x0 引数の形式で x を渡します。たとえば、x0 が 5 行 3 列の配列の場合、fminimax は 5 行 3 列の配列として x を fun に渡します。ただし、fminimax は、x を列ベクトル x(:) に変換してから、線形制約行列 A または Aeq を x と乗算します。

ベクトル F(x) の一部の要素の最悪値の絶対値を最小化するには (すなわち min{max abs{F(x)} })、これらの目的関数を F の最初の要素に設定し、optimoptions を使って AbsoluteMaxObjectiveCount オプションをこれらの目的関数の数に設定してください。これらの目的関数を fun が返すベクトル F の最初の要素に割り当て "なければなりません"。例については、1 つの目的関数の絶対値を使用したミニマックス問題の解法を参照してください。

また目的関数の勾配を計算することもでき、"さらに" 次のように SpecifyObjectiveGradient オプションが true であると仮定します。

options = optimoptions('fminimax','SpecifyObjectiveGradient',true)

この場合、関数 fun は 2 番目の出力引数に x での勾配値 G (行列) を返さなければなりません。勾配は点 x における各 F の偏導関数 dF/dx です。F が長さ m のベクトルであり、x の長さが n で、n が x0 の長さである場合、F(x) の勾配 G は n 行 m 列の行列です。ここで G(i,j) は F(j) の x(i) に関する偏導関数です (すなわち、G の第 j 番目の列が j 番目の目的関数 F(j) の勾配です)。F を配列として定義する場合、上記の考察は F(:)、すなわち配列 F の線形順序に適用されます。どのような場合でも、G は 2 次元行列です。

メモ

SpecifyObjectiveGradient を true に設定することは、問題に非線形制約がない場合と、問題の非線形制約の SpecifyConstraintGradient が true の場合のみ有効です。内部的に目的関数が制約に含まれるため、ソルバーは、勾配推定を避けるために両方の勾配 (目的関数と制約) が指定されていることを必要とします。

データ型: char | string | function_handle

x0 — 初期点

実数ベクトル | 実数配列

初期点。実数ベクトルまたは実数配列として指定されます。ソルバーは、x0 の要素数および x0 のサイズを使用して、fun が受け入れる変数の数およびサイズを決定します。

例: x0 = [1,2,3,4]

データ型: double

A — 線形不等式制約

実数行列

実数行列として指定される線形不等式制約です。A は M 行 N 列の行列で、M は不等式の数、N は変数の数 (x0 の要素数) です。スパース データをサポートするアルゴリズムを使用する大規模な問題の場合は、A をスパース行列として渡します。最適化アルゴリズムのスパース性を参照してください。

A は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は N 個の変数 x(:) の列ベクトル、b は M 個の要素をもつ列ベクトルです。

たとえば、次の不等式を考えてみましょう。

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

次の制約を入力することによって、不等式を指定します。

A = [1,2;3,4;5,6];
b = [10;20;30];

例: x の成分の和が 1 以下であることを指定するには、A = ones(1,N) と b = 1 を使用します。

データ型: single | double

b — 線形不等式制約

実数ベクトル

実数ベクトルで指定される線形不等式制約です。b は、行列 A に関連する M 要素ベクトルです。b を行ベクトルとして渡す場合、ソルバーは b を列ベクトル b(:) に内部的に変換します。

b は M 個の線形不等式を符号化します。

A*x <= b,

ここで、x は N 個の変数 x(:) の列ベクトル、A は M 行 N 列の行列です。

たとえば、次の不等式を考えてみましょう。

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30.

次の制約を入力することによって、不等式を指定します。

A = [1,2;3,4;5,6];
b = [10;20;30];

例: x の成分の和が 1 以下であることを指定するには、A = ones(1,N) と b = 1 を使用します。

データ型: single | double

Aeq — 線形等式制約

実数行列

実数行列として指定される線形等式制約です。Aeq は Me 行 N 列の行列で、Me は等式の数、N は変数の数 (x0 の要素数) です。スパース データをサポートするアルゴリズムを使用する大規模な問題の場合は、A をスパース行列として渡します。最適化アルゴリズムのスパース性を参照してください。

Aeq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、beq は Me 個の要素をもつ列ベクトルです。

たとえば、次の不等式を考えてみましょう。

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20,

次の制約を入力することによって、不等式を指定します。

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: x の成分の和が 1 であることを指定するには、Aeq = ones(1,N) と beq = 1 を使用します。

データ型: single | double

beq — 線形等式制約

実数ベクトル

実数ベクトルで指定される線形等式制約です。beq は、行列 Aeq に関連する Me 要素ベクトルです。beq を行ベクトルとして渡す場合、ソルバーは beq を列ベクトル beq(:) に内部的に変換します。

beq は Me 個の線形等式を符号化します。

Aeq*x = beq,

ここで、x は N 個の変数 x(:) の列ベクトル、Aeq は Me 行 N 列の行列です。

たとえば、次の等式を考えてみましょう。

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20.

次の制約を入力することによって、等式を指定します。

Aeq = [1,2,3;2,4,1];
beq = [10;20];

例: x の成分の和が 1 であることを指定するには、Aeq = ones(1,N) と beq = 1 を使用します。

データ型: single | double

lb — 下限

実数ベクトル | 実数配列

下限。実数ベクトルまたは実数配列として指定されます。x0 の要素数と lb の要素数が等しい場合、lb は次を指定します。

x(i) >= lb(i) (すべての i について)

numel(lb) < numel(x0) の場合、lb は次を指定します。

x(i) >= lb(i) (1 <= i <= numel(lb))

lb の要素数が x0 より少ない場合、ソルバーは警告を生成します。

例: x のすべての成分が正であることを指定するには、lb = zeros(size(x0)) を使用します。

データ型: single | double

ub — 上限

実数ベクトル | 実数配列

実数ベクトルまたは実数配列として指定される上限です。x0 の要素数と ub の要素数が等しい場合、ub は次を指定します。

x(i) <= ub(i) (すべての i について)

numel(ub) < numel(x0) の場合、ub は次を指定します。

x(i) <= ub(i) (1 <= i <= numel(ub))

ub の要素数が x0 より少ない場合、ソルバーは警告を生成します。

例: x のすべての成分が 1 未満であることを指定するには、ub = ones(size(x0)) を使用します。

データ型: single | double

nonlcon — 非線形制約

関数ハンドル | 関数名

非線形制約。関数ハンドルまたは関数名として指定されます。nonlcon は、ベクトルまたは配列 x を受け、2 つの配列 c(x) および ceq(x) を返す関数です。

• c(x) は、x での非線形不等式制約の配列です。fminimax は次の条件を満たそうとします。

  c(x) <= 0 for all entries of c.

• ceq(x) は、x での非線形等式制約の配列です。fminimax は次の条件を満たそうとします。

  ceq(x) = 0 for all entries of ceq.

以下に例を示します。

x = fminimax(@myfun,x0,...,@mycon)

ここで mycon は次のような MATLAB 関数です。

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

また制約関数の勾配を計算することができ、"さらに" 次のように SpecifyConstraintGradient オプションが true であるとします。

options = optimoptions('fminimax',SpecifyConstraintGradient=true)

この場合、関数 nonlcon は 3 番目および 4 番目の出力引数に c(x) の勾配 GC および ceq(x) の勾配 GCeq を返さなければなりません。与えられた勾配を受け付けないソルバーに使用する勾配を条件付ける方法の説明は、非線形制約を参照してください。

nonlcon が m 成分のベクトル c を返し、x の長さが n で、n が x0 の長さである場合、c(x) の勾配 GC は n 行 m 列の行列です。ここで GC(i,j) は c(j) の x(i) に関する偏導関数です (すなわち、GC の第 j 列が j 番目の不等式制約 c(j) の勾配です)。ceq が p 個の成分をもち、ceq(x) の勾配 GCeq が n 行 p 列の行列である場合も同様です。このとき、GCeq(i,j) は ceq(j) の x(i) に関する偏導関数です (すなわち、GCeq の第 j 列が j 番目の等式制約 ceq(j) の勾配です)。

メモ

SpecifyConstraintGradient の true への設定は SpecifyObjectiveGradient が true に設定されている場合のみ効果的です。内部的に目的関数が制約に含まれるため、ソルバーは、勾配推定を避けるために両方の勾配 (目的関数と制約) が指定されていることを必要とします。

メモ:

Optimization Toolbox™ の関数が double 型の入力のみを受け入れるため、ユーザーが指定した目的関数と非線形制約関数は double 型の出力を返さなければなりません。

必要に応じて非線形制約関数 nonlcon をパラメーター化する方法については、追加パラメーターの受け渡しを参照してください。

データ型: char | function_handle | string

options — 最適化オプション

optimoptions の出力 | optimset などによって返される構造体

最適化オプション。optimoptions の出力、または optimset などによって返される構造体として指定されます。

一部のオプションは、optimoptions に表示されません。このようなオプションは、次の表ではイタリックで示されています。詳細については、最適化オプションの表示を参照してください。

optimset の名前が異なるオプションの詳細については、新旧のオプション名を参照してください。

オプション	説明
AbsoluteMaxObjectiveCount	Fi の最大絶対値を最小にする Fi(x) の要素の数。1 つの目的関数の絶対値を使用したミニマックス問題の解法を参照してください。 optimset の場合、名前は MinAbsMax です。
ConstraintTolerance	制約違反に関する終了許容誤差 (非負のスカラー)。既定値は 1e-6 です。許容誤差と停止条件を参照してください。 optimset の場合、名前は TolCon です。
Diagnostics	最小化または求解する関数に関する情報を表示します。選択肢は 'on' または 'off' (既定の設定) です。
DiffMaxChange	有限差分勾配を計算する場合に変数内で生じる最大変化量です (正のスカラー)。既定値は Inf です。
DiffMinChange	有限差分勾配を計算する場合に変数内で生じる最小変化量です (正のスカラー)。既定値は 0 です。
Display	表示レベル (反復表示を参照): 'off' または 'none' — 出力を表示しない。 'iter' — 各反復の出力を表示し、既定の終了メッセージを与える。 'iter-detailed' — 各反復の出力を表示し、技術的な終了メッセージを与える。 'notify' — 関数が収束しない場合にのみ出力を表示し、既定の終了メッセージを与える。 'notify-detailed' — 関数が収束しない場合にのみ出力を表示し、技術的な終了メッセージを与える。 'final' (既定の設定) — 最終出力のみを表示し、既定の終了メッセージを与える。 'final-detailed' — 最終出力のみを表示し、技術的な終了メッセージを与える。
FiniteDifferenceStepSize	有限差分のスカラーまたはベクトルのステップ サイズ ファクター。FiniteDifferenceStepSize をベクトル v に設定すると、前方有限差分 delta は次のようになります。 delta = v.*sign′(x).*max(abs(x),TypicalX); ここで、sign′(0) = 1 を除き sign′(x) = sign(x) です。中心有限差分は次のようになります。 delta = v.*max(abs(x),TypicalX); スカラー FiniteDifferenceStepSize はベクトルに展開されます。既定値は、前進有限差分法では sqrt(eps)、中心有限差分法では eps^(1/3) です。 optimset の場合、名前は FinDiffRelStep です。
FiniteDifferenceType	勾配推定に使用される有限差分のタイプは 'forward' (既定の設定) または 'central' (中心) のいずれかです。'central' では 2 倍の関数評価が必要になりますが、一般的に正確性が増します。 アルゴリズムは有限差分の両方のタイプを推定するとき、範囲に注意深く従います。たとえば、forward 差分ではなく、backward 差分を選択すると、範囲外の点を計算しないようにすることができます。 optimset の場合、名前は FinDiffType です。
FunctionTolerance	関数値に関する終了許容誤差 (非負のスカラー)。既定値は 1e-6 です。許容誤差と停止条件を参照してください。 optimset の場合、名前は TolFun です。
FunValCheck	目的関数値と制約値が有効であるかどうかをチェックします。'on' は目的関数または制約が complex、Inf、または NaN の値を返した場合にエラーを表示します。既定の 'off' ではエラーを表示しません。
MaxFunctionEvaluations	関数評価の最大許容回数 (非負の整数)。既定値は 100*numberOfVariables です。詳細については、許容誤差と停止条件および反復と関数カウントを参照してください。 optimset の場合、名前は MaxFunEvals です。
MaxIterations	反復の最大許容回数 (非負の整数)。既定値は 400 です。詳細については、許容誤差と停止条件および反復と関数カウントを参照してください。 optimset の場合、名前は MaxIter です。
MaxSQPIter	SQP 反復の最大数 (正の整数)。既定値は 10*max(numberOfVariables, numberOfInequalities + numberOfBounds) です。
MeritFunction	このオプションを 'multiobj' (既定の設定) に設定した場合、ゴール到達メリット関数またはミニマックス メリット関数を使用します。このオプションを 'singleobj' に設定した場合、メリット関数 fmincon を使用します。
OptimalityTolerance	1 次の最適性に関する終了許容誤差 (非負のスカラー)。既定値は 1e-6 です。1 次の最適性の尺度を参照してください。 optimset の場合、名前は TolFun です。
OutputFcn	各反復で最適化関数が呼び出す 1 つ以上のユーザー定義の関数。関数ハンドルか、関数ハンドルの cell 配列を渡します。既定の設定はなし ([]) です。出力関数とプロット関数の構文を参照してください。
PlotFcn	アルゴリズム実行時における、進行状態の各種測定値を示すプロット。定義済みのプロットから選択するか、自身で記述します。名前、関数ハンドル、または名前か関数ハンドルの cell 配列を渡します。カスタム プロット関数の場合は、関数ハンドルを渡します。既定の設定はなし ([]) です。 'optimplotx' は現在の点をプロットします。 'optimplotfunccount' は関数カウントをプロットします。 'optimplotfval' は目的関数値をプロットします。 'optimplotconstrviolation' は最大制約違反をプロットします。 'optimplotstepsize' はステップ サイズをプロットします。 カスタムのプロット関数は、出力関数と同じ構文を使用します。詳細については、Optimization Toolbox の出力関数および出力関数とプロット関数の構文を参照してください。 optimset の場合、名前は PlotFcns です。
RelLineSrchBnd	x の変位合計が |Δx(i)| ≤ RelLineSrchBnd· max(|x(i)|,|typicalx(i)|) を満たすような、直線探索ステップ長の相対範囲 (実数の非負のスカラー値)。このオプションはソルバーが大きすぎるステップをとった場合に、x の変位の大きさをコントロールします。既定の設定はなし ([]) です。
RelLineSrchBndDuration	RelLineSrchBnd で範囲を指定された反復数が有効になります。既定値は 1 です。
SpecifyConstraintGradient	ユーザーにより定義される非線形制約関数に対する勾配。nonlcon で説明されているように、このオプションが true に設定されている場合、fminimax では制約関数に 4 つの出力を求めるようになります。このオプションを false (既定の設定) に設定すると、fminimax は有限差分を使用して非線形制約の勾配を推定します。 optimset の場合、名前は GradConstr で、値は 'on' または 'off' です。
SpecifyObjectiveGradient	ユーザーが定義する目的関数の勾配。勾配の定義方法については、fun の説明を参照してください。このオプションを true に設定すると、fminimax は目的関数のユーザー定義の勾配を使用します。既定の false の場合、fminimax は有限差分を使用して勾配を推定します。 optimset の場合、名前は GradObj で、値は 'on' または 'off' です。
StepTolerance	x に関する終了許容誤差 (非負のスカラー)。既定値は 1e-6 です。許容誤差と停止条件を参照してください。 optimset の場合、名前は TolX です。
TolConSQP	内部反復 SQP 制約違反に関する終了許容誤差 (正のスカラー)。既定値は 1e-6 です。
TypicalX	典型的な x の値です。TypicalX の要素数は、開始点 x0 の要素数と等しくなります。既定値は ones(numberofvariables,1) です。関数 fminimax は TypicalX を使用して勾配推定の有限差分をスケーリングします。
UseParallel	並列計算を使用するためのオプション。このオプションが true に設定されている場合、fminimax は並列で勾配を推定します。既定値は false です。並列計算を参照してください。

例: optimoptions('fminimax','PlotFcn','optimplotfval')

problem — 問題構造体

構造体

問題構造体。次の表のフィールドをもつ構造体として指定します。

フィールド名	エントリ
objective	目的関数 fun
x0	x の初期点
Aineq	線形不等式制約の行列
bineq	線形不等式制約のベクトル
Aeq	線形等式制約の行列
beq	線形等式制約のベクトル
lb	下限のベクトル
ub	上限のベクトル
nonlcon	非線形制約関数
solver	'fminimax'
options	optimoptions で作成されたオプション

problem 構造体では、少なくとも objective、x0、solver、および options フィールドを指定しなければなりません。

データ型: struct

出力引数

x — 解

実数ベクトル | 実数配列

実数ベクトルまたは実数配列として返される解です。x のサイズは、x0 のサイズと同じです。通常、exitflag が正の場合、x は問題に対する局所的な解になります。解の質の詳細については、ソルバーが成功する場合を参照してください。

fval — 解での目的関数値

実数配列

解での目的関数値。実数配列として返されます。一般的に、fval = fun(x) になります。

maxfval — 解での目的関数値の最大値

実数スカラー

解での目的関数値の最大値。実数スカラーとして返されます。maxfval = max(fval(:))。

exitflag — fminimax の停止理由

整数

fminimax の停止理由。整数として返されます。

1	関数が解 x に収束したことを示します。
4	探索方向の大きさが指定した許容誤差より小さく、制約違反が options.ConstraintTolerance より小さいことを示します。
5	方向導関数の大きさが指定した許容誤差より小さく、制約違反が options.ConstraintTolerance より小さいことを示します。
0	反復回数が options.MaxIterations を超過、または関数評価の回数が options.MaxFunctionEvaluations を超過しています。
-1	出力関数またはプロット関数によって停止したことを示します。
-2	実行可能な点が見つかりません。

output — 最適化プロセスに関する情報

構造体

最適化プロセスに関する情報。次の表のフィールドをもつ構造体として返されます。

iterations	実行した反復回数
funcCount	関数評価の回数
lssteplength	探索方向に対する直線探索ステップのサイズ
constrviolation	制約関数の最大値
stepsize	x の最終ステップ サイズ
algorithm	使用される最適化アルゴリズム
firstorderopt	1 次の最適性の尺度
message	終了メッセージ

lambda — 解におけるラグランジュ乗数

構造体

解におけるラグランジュ乗数。次の表のフィールドをもつ構造体として返されます。

lower	lb に対応する下限
upper	ub に対応する上限
ineqlin	A および b に対応する線形不等式
eqlin	Aeq および beq に対応する線形等式
ineqnonlin	nonlcon の c に対応する非線形不等式
eqnonlin	nonlcon の ceq に対応する非線形等式

アルゴリズム

fminimax は、ゴール到達問題に変換し、変換されたゴール到達問題を fgoalattain を使用して解くことによって、ミニマックス問題を解きます。変換によってすべてのゴールが 0、すべての重みが 1 に設定されます。多目的関数の最適化アルゴリズムの式 1を参照してください。

代替機能

アプリ

[最適化] ライブ エディター タスクが fminimax にビジュアル インターフェイスを提供します。

拡張機能

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

並列実行するには、'UseParallel' オプションを true に設定します。

options = optimoptions('solvername','UseParallel',true)

詳細については、Optimization Toolbox での並列計算の使用を参照してください。

バージョン履歴

R2006a より前に導入

参考

fgoalattain | optimoptions | 最適化

トピック

• 関数ハンドルの作成
• 多目的最適化