fminimax と fminunc の比較

ミニマックス問題は、一連の目的関数の最大値を最小化します。この最大値の関数、すなわちスカラー関数を最小化しないのはなぜでしょうか。それは、最大値が滑らかではなく、fminunc などの Optimization Toolbox™ ソルバーでは平滑性が必要であるためです。

たとえば、fun(x) を 2 変数の 3 つの線形目的関数として、fun2 をこれら 3 つの目的関数の最大値として定義します。

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];
fun2 = @(x)max(fun(x),[],2);

3 つの目的関数の最大値をプロットします。

[X,Y] = meshgrid(linspace(-5,5));
Z = fun2([X(:),Y(:)]);
Z = reshape(Z,size(X));
surf(X,Y,Z,'LineStyle','none')
view(-118,28)

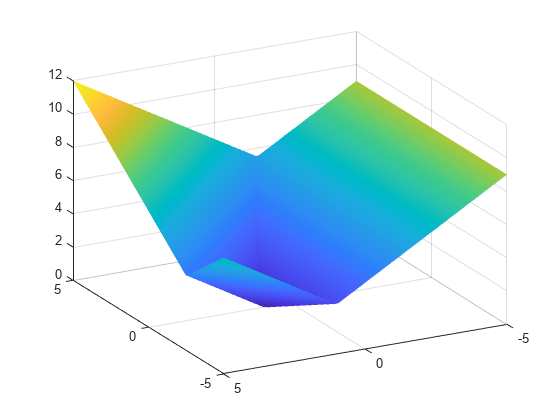
fminimax ではミニマックス点が簡単に見つかります。

x0 = [0,0];
[xm,fvalm,maxfval] = fminimax(fun,x0)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

xm = 1×2

   -2.5000    2.2500

fvalm = 1×3

    1.7500    1.7500    1.7500

maxfval = 1.7500

しかし、fminunc は、ミニマックス点から離れた点で停止します。

[xu,fvalu] = fminunc(fun2,x0)

Local minimum possible.

fminunc stopped because it cannot decrease the objective function
along the current search direction.

xu = 1×2

         0    1.0000

fvalu = 3.0000

fminimax ではより良い (小さい) 解が見つかります。

fprintf("fminimax finds a point with objective %g,\nwhile fminunc finds a point with objective %g.",maxfval,fvalu)

fminimax finds a point with objective 1.75,
while fminunc finds a point with objective 3.

参考

fminimax

関連するトピック

• 多目的最適化
• 滑らかでない関数の滑らかな定式化