Optimization Toolbox の出力関数

出力関数とは

反復ごとに、最適化アルゴリズムの出力を得たい場合を考えてみましょう。たとえば、アルゴリズムが計算する一連の点を探し、プロットしたい場合があります。これを行うには、最適化関数が各反復で呼び出す出力関数を作成します。詳細と構文については出力関数とプロット関数の構文を参照してください。

この例では、出力関数にソルバーベースのアプローチを使用します。問題ベースのアプローチについては、問題ベースの最適化の出力関数を参照してください。

一般に出力関数を使用するソルバーは、入力に非線形関数を指定できます。関数リファレンスページの「オプション」セクションを参照すると、どのソルバーが出力関数を使用できるのかがわかります。

出力関数の使用

この例では、出力関数を使用して fmincon 解法プロセスをモニターし、制約付き非線形最適化問題を解く方法を示します。出力関数は、各 fmincon 反復の終了時点で次の処理を実行します。

現在の点をプロットします。
現在の点とそれに対応する目的関数値を history という名前の変数に保存し、現在の探索方向を searchdir という名前の変数に保存します。探索方向は現在の点から次の点までの方向ベクトルです。

加えて、関数 fmincon の外部で履歴を使用可能にするために、fmincon を呼び出し、出力関数の変数を返す入れ子関数内で最適化を実行します。この情報伝達方法の詳細については、追加パラメーターの受け渡しを参照してください。補助関数 runfmincon (この例の最後に記載) に、入れ子関数の呼び出しが含まれています。

目的関数と制約関数

問題は、次の関数を最小化することです。

$f (x) = \exp (x_{1}) (4 x_{1}^{2} + 2 x_{2}^{2} + 4 x_{1} x_{2} + 2 x_{2} + 1)$

これには、非線形不等式制約が適用されます。

$\begin{array}{l} x_{1} + x_{2} - x_{1} x_{2} \geq 3 / 2 \\ x_{1} x_{2} \geq - 10 . \end{array}$

関数 objfun (runfmincon の入れ子) が目的関数を実装します。関数 confun (runfmincon の入れ子) が制約関数を実装します。

ソルバーの呼び出し

問題に対する解を取得して、fmincon 反復の履歴を表示するには、関数 runfmincon を呼び出します。

[xsol,fval,history,searchdir] = runfmincon;

                                Max     Line search  Directional  First-order 
 Iter F-count        f(x)   constraint   steplength   derivative   optimality Procedure 
    0      3       1.8394          0.5                                         Infeasible start point
    1      6      1.85127     -0.09197            1        0.109        0.778   
    2      9     0.300167         9.33            1       -0.117        0.313  Hessian modified twice  
    3     12     0.529835       0.9209            1         0.12        0.232   
    4     16     0.186965       -1.517          0.5       -0.224         0.13   
    5     19    0.0729085       0.3313            1       -0.121        0.054   
    6     22    0.0353323     -0.03303            1      -0.0542       0.0271   
    7     25    0.0235566     0.003184            1      -0.0271      0.00587   
    8     28    0.0235504    9.035e-08            1      -0.0146     8.51e-07   
Active inequalities (to within options.ConstraintTolerance = 1e-06):
  lower      upper     ineqlin   ineqnonlin
                                     1
                                     2

Figure contains an axes object. The axes object with title Sequence of Points Computed by fmincon contains 18 objects of type line, text.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the  value of the constraint tolerance.

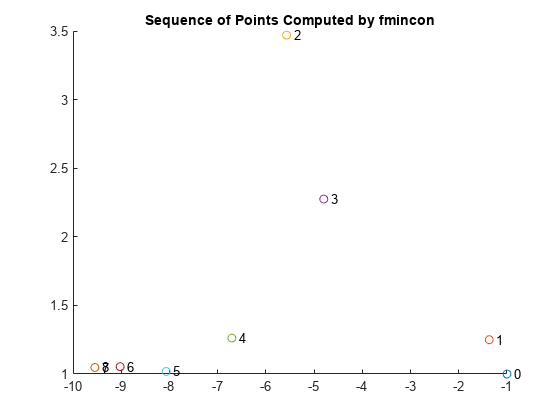
出力関数は、fmincon が評価する点のプロットを作成します。各点には反復回数のラベルが付けられます。最適な点は 8 回目の反復で求まります。点列の最後の 2 つの点は非常に近いため重なって表示されます。

出力 history は 2 つのフィールドからなる構造体です。

disp(history)

       x: [9x2 double]
    fval: [9x1 double]

history の fval フィールドには、fmincon が計算した点列に対応する目的関数値が含まれています。

disp(history.fval)

これらは、ヘッダーが f(x) の列の反復出力に表示される値と同じ値です。

history の x フィールドには、fmincon が計算した点列が含まれています。

disp(history.x)

   -1.0000    1.0000
   -1.3679    1.2500
   -5.5708    3.4699
   -4.8000    2.2752
   -6.7054    1.2618
   -8.0679    1.0186
   -9.0230    1.0532
   -9.5471    1.0471
   -9.5474    1.0474

searchdir の出力は各反復での fmincon の探索方向を含みます。探索方向は、現在の反復で計算された点から次の反復で計算される点までの変位を示すベクトルです。

disp(searchdir)

   -0.3679    0.2500
   -4.2029    2.2199
    0.7708   -1.1947
   -3.8108   -2.0268
   -1.3625   -0.2432
   -0.9552    0.0346
   -0.5241   -0.0061
   -0.0003    0.0003

補助関数

次のコードは、出力関数 outfun、目的関数 objfun、および非線形制約関数 confun を入れ子関数として含む、関数 runfmincon を作成します。

function [xsol,fval,history,searchdir] = runfmincon
 
% Set up shared variables with outfun
history.x = [];
history.fval = [];
searchdir = [];
 
% Call optimization
x0 = [-1 1];
options = optimoptions(@fmincon,'OutputFcn',@outfun,... 
    'Display','iter','Algorithm','active-set');
[xsol,fval] = fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options);
 
 function stop = outfun(x,optimValues,state)
     stop = false;
 
     switch state
         case 'init'
             hold on
         case 'iter'
         % Concatenate current point and objective function
         % value with history. x must be a row vector.
           history.fval = [history.fval; optimValues.fval];
           history.x = [history.x; x];
         % Concatenate current search direction with 
         % searchdir.
           searchdir = [searchdir;... 
                        optimValues.searchdirection'];
           plot(x(1),x(2),'o');
         % Label points with iteration number and add title.
         % Add .15 to x(1) to separate label from plotted 'o'.
           text(x(1)+.15,x(2),... 
                num2str(optimValues.iteration));
           title('Sequence of Points Computed by fmincon');
         case 'done'
             hold off
         otherwise
     end
 end
 
 function f = objfun(x)
     f = exp(x(1))*(4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) +... 
                    2*x(2) + 1);
 end
 
 function [c, ceq] = confun(x)
     % Nonlinear inequality constraints
     c = [1.5 + x(1)*x(2) - x(1) - x(2);
         -x(1)*x(2) - 10];
     % Nonlinear equality constraints
     ceq = [];
 end
end