pagemrdivide

ページ単位の行列の右除算

R2022a 以降

ページ内をすべて折りたたむ

構文

X = pagemrdivide(B,A)
X = pagemrdivide(B,A,transpA)
[X,rcondA] = pagemrdivide(___)

説明

X = pagemrdivide(B,A) は、N 次元配列 A の各ページと N 次元配列 B の各ページの行列の右除算を計算します。出力配列 X の各ページは X(:,:,i) = B(:,:,i) / A(:,:,i) で与えられます。B と A のページは、mrdivide (/) に対する有効な入力でなければなりません。

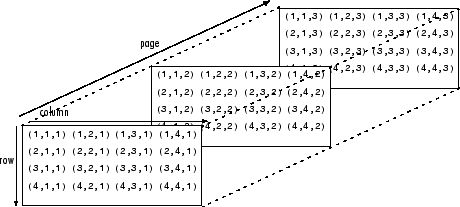
B および A が 3 次元より大きい場合、最初の 2 次元を超える次元はすべて互換性のあるサイズでなければなりません。pagemrdivide は、余分な次元を暗黙的に拡張し、X(:,:,i,j,k) = B(:,:,i,j,k) / A(:,:,i,j,k) のように、すべてのページの組み合わせを除算します。

例

X = pagemrdivide(B,A,transpA) は、A の各ページに対してオプションで転置を適用します。transpA の値は、"transpose"、"ctranspose"、または "none" のいずれかになります。たとえば、pagemrdivide(B,A,"transpose") は X(:,:,i) = B(:,:,i) / A(:,:,i).' を計算します。

例

[X,rcondA] = pagemrdivide(___) は、前述の構文の任意の入力引数の組み合わせを使用して、A の各ページの条件数の逆数の推定値も返します。rcondA(1,1,i) < eps の場合、X(:,:,i) = B(:,:,i) / A(:,:,i) は行列が悪条件であるため警告を返します。ただし、pagemrdivide は悪条件の入力に対して警告を発行しません。

例

例

すべて折りたたむ

ライブ スクリプトを開く

2 つのページのそれぞれに 3 行 3 列の行列を含む 3×3×2 の配列 A を作成します。さらに、1×3×2 の配列 B を作成します。

p1 = magic(3);
p2 = hilb(3);
A = cat(3,p1,p2)
A = 
A(:,:,1) =

     8     1     6
     3     5     7
     4     9     2


A(:,:,2) =

    1.0000    0.5000    0.3333
    0.5000    0.3333    0.2500
    0.3333    0.2500    0.2000


B = ones(1,3,2)
B = 
B(:,:,1) =

     1     1     1


B(:,:,2) =

     1     1     1

A と B の対応する各ページのセットについて方程式 X(:,:,i)*A(:,:,i) = B(:,:,i) の解を求めます。

X = pagemrdivide(B,A)
X = 
X(:,:,1) =

    0.0667    0.0667    0.0667


X(:,:,2) =

    3.0000  -24.0000   30.0000
ライブ スクリプトを開く

2 つのページのそれぞれに 4 行 4 列の行列を含む 4×4×2 の配列 A を作成します。さらに、1×4×2 の配列 B を作成します。

p1 = pascal(4);
p2 = magic(4);
A = cat(3,p1,p2)
A = 
A(:,:,1) =

     1     1     1     1
     1     2     3     4
     1     3     6    10
     1     4    10    20


A(:,:,2) =

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1


B = 2*ones(1,4,2)
B = 
B(:,:,1) =

     2     2     2     2


B(:,:,2) =

     2     2     2     2

"transpose" オプションを指定して、A と B の対応する各ページのセットについて方程式系 X(:,:,i)*A(:,:,i).' = B(:,:,i) の解を求めます。

X = pagemrdivide(B,A,"transpose")
X = 
X(:,:,1) =

     2     0     0     0


X(:,:,2) =

    0.1176    0.2353   -0.1176         0
ライブ スクリプトを開く

2 つのページのそれぞれに 10 行 10 列の行列を含む 10×10×2 の配列 A を作成します。さらに、1×10×2 の配列 B を作成します。

p1 = diag([ones(9,1);0]);
p2 = pascal(10);
A = cat(3,p1,p2)
A = 
A(:,:,1) =

     1     0     0     0     0     0     0     0     0     0
     0     1     0     0     0     0     0     0     0     0
     0     0     1     0     0     0     0     0     0     0
     0     0     0     1     0     0     0     0     0     0
     0     0     0     0     1     0     0     0     0     0
     0     0     0     0     0     1     0     0     0     0
     0     0     0     0     0     0     1     0     0     0
     0     0     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     0     0     0     0


A(:,:,2) =

           1           1           1           1           1           1           1           1           1           1
           1           2           3           4           5           6           7           8           9          10
           1           3           6          10          15          21          28          36          45          55
           1           4          10          20          35          56          84         120         165         220
           1           5          15          35          70         126         210         330         495         715
           1           6          21          56         126         252         462         792        1287        2002
           1           7          28          84         210         462         924        1716        3003        5005
           1           8          36         120         330         792        1716        3432        6435       11440
           1           9          45         165         495        1287        3003        6435       12870       24310
           1          10          55         220         715        2002        5005       11440       24310       48620


B = 3*ones(1,10,2)
B = 
B(:,:,1) =

     3     3     3     3     3     3     3     3     3     3


B(:,:,2) =

     3     3     3     3     3     3     3     3     3     3

A と B の対応する各ページのセットについて方程式 X(:,:,i)*A(:,:,i) = B(:,:,i) の解を求めます。2 つの出力を指定して、A の各ページの条件数の逆数も返します。

[X,rcondA] = pagemrdivide(B,A)
X = 
X(:,:,1) =

   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   Inf


X(:,:,2) =

     3     0     0     0     0     0     0     0     0     0


rcondA = 
rcondA(:,:,1) =

     0


rcondA(:,:,2) =

   1.2295e-10

条件数の逆数を eps と比較します。この結果は、最初のページの行列が悪条件であることを示しています。コマンド B(:,:,1)/A(:,:,1) で警告が返され、そのページの演算の結果は信頼できません。

rcondA < eps
ans = 1×1×2 logical array
ans(:,:,1) =

   1


ans(:,:,2) =

   0

入力引数

すべて折りたたむ

入力配列。B と A は、対応する各ページのセット B(:,:,i,...) と A(:,:,i,...) が mrdivide に対する有効な入力である多次元配列です。

B および A が 3 次元より大きい場合、最初の 2 次元を超える次元はすべて互換性のあるサイズでなければなりません。pagemrdivide は、余分な次元を暗黙的に拡張し、X(:,:,i,j,k) = B(:,:,i,j,k) / A(:,:,i,j,k) のように、すべてのページの組み合わせを除算します。

データ型: single | double
複素数のサポート: あり

A の転置オプション。次の値のいずれかとして指定します。

値説明
"none"A を転置しません。これは既定値です。
"transpose"A の各ページを複素共役なしで転置します。
"ctranspose"A の各ページを複素共役を使用して転置します。

例: pagemrdivide(B,A,"transpose")

出力引数

すべて折りたたむ

線形方程式系の解。B および A と同じ数のページをもつ多次元配列として返されます。X の各ページは線形方程式系 X(:,:,i,...) = B(:,:,i,...) / A(:,:,i,...) の解になります。

A の条件数の逆数の推定値。多次元配列として返されます。A のページが m 行 n 列の方形行列 (m~=n) の場合、rcondA は QR 分解の R の要素を使用して推定されます。rcondA(1,1,i) < eps の場合、X(:,:,i) = B(:,:,i) / A(:,:,i) は行列が悪条件であるため警告を返します。ただし、pagemrdivide は悪条件の入力に対して警告を発行しません。

rcondA は、rcond 関数の結果と同じでない場合があります。

詳細

すべて折りたたむ

ヒント

  • pagemrdivide を使用して取得した結果は、for ループで同じ各行列を使用して線形システムの解を計算することと数値的に等価です。ただし、浮動小数点の丸め誤差のため、2 つの結果が若干異なることがあります。

拡張機能

すべて展開する

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2022a で導入

すべて展開する

参考

| | | |

トピック