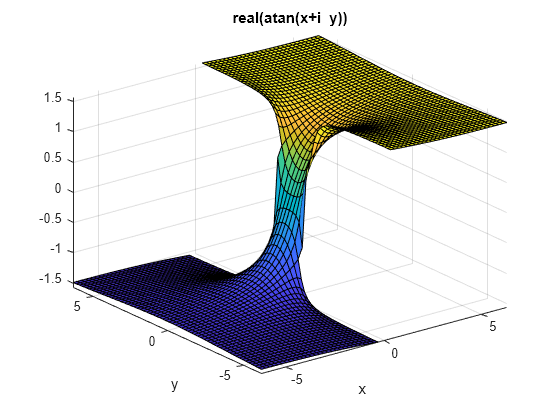
ezsurf

(非推奨) 簡単な 3 次元カラー表面プロット

ezsurf は推奨されません。代わりに fsurf を使用してください。詳細については、バージョン履歴を参照してください。

構文

ezsurf(f)

ezsurf(f,xyinterval)

ezsurf(funx,funy,funz)

ezsurf(funx,funy,funz,uvinterval)

ezsurf(___,n)

ezsurf(___,'circ')

ezsurf(ax,___)

s = ezsurf(___)

説明

ezsurf(f) は、関数 surf を使用して、関数 f(x,y) の表面プロットを作成します。x と y の既定の区間 [-2π 2π] での f をプロットします。

ezsurf は、タイトルと軸ラベルをプロットに自動的に追加します。

ezsurf(f,xyinterval) は、指定された区間でプロットします。

ezsurf(funx,funy,funz) は、u と v の既定の区間 [-2π 2π] での、パラメトリックな表面 funx(u,v)、funy(u,v)、および funz(u,v) をプロットします。

ezsurf(funx,funy,funz,uvinterval) は、指定された区間を使用してパラメトリックな表面をプロットします。

ezsurf(___,n) は、n 行 n 列のグリッドを使用してプロットします。このオプションは、前述の構文における任意の入力引数が組み合わされてから使用します。

ezsurf(___,'circ') は、区間の中心に配置された円盤でプロットします。

ezsurf(ax,___) は、現在の座標軸ではなく、ax で指定される座標軸にプロットします。前述のいずれかの構文で、任意の入力引数の組み合わせの前に座標軸を指定します。

s = ezsurf(___) は chart surface オブジェクトを返します。表面を作成した後で変更を加えるには、s を使用します。プロパティの一覧については、Surface のプロパティ を参照してください。

例

数学関数の表面プロット

関数 $\mathit{f}\left(\mathit{x},\mathit{y}\right)=\mathrm{real}\left(\mathrm{atan}\left(\mathit{x}+\mathit{iy}\right)\right)$ を領域 $$-2\pi <x<2\pi$$ および $$-2\pi <y<2\pi$$ でプロットします。関数 ezsurf は数学関数が定義されない点をプロットしません。これらの点はプロットされないように NaN に設定されます。

figure
ezsurf('real(atan(x+i*y))')

surf を使用して、不連続点をフィルター処理せずに同じデータをプロットします。

figure
[x,y] = meshgrid(linspace(-2*pi,2*pi,60));
z = real(atan(x+1i.*y));
surf(x,y,z)

入力引数

f — プロット対象の 3 次元関数

文字ベクトル | string スカラー | 関数ハンドル

プロット対象の 3 次元関数。文字ベクトル、string スカラー、あるいは名前付き関数または無名関数の関数ハンドルとして指定します。

z = f(x,y) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。

関数を文字ベクトルまたは string スカラーとして指定する場合、配列の乗算、除算、およびべき乗が常に暗黙的に指定されます。たとえば、x^2 は x.^2 と解釈されます。

例: 'sqrt(x^2 + y^2)'

関数を関数ハンドルとして指定する場合に最高のパフォーマンスを得るには、行列演算子ではなく配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: @(x,y) sin(x).*cos(y)

xyinterval — x および y のプロット区間

[-2π 2π -2π 2π] (既定値) | [min max] 形式のベクトル | [xmin xmax ymin ymax] 形式のベクトル

x および y のプロット区間。次のいずれかの形式で指定します。

• [min max] 形式のベクトル — x および y の両方に区間 [min max] を使用します。

• [xmin xmax ymin ymax] 形式のベクトル — x に区間 [xmin xmax]、y に区間 [ymin ymax] を使用します。

funx — x 座標のパラメトリック関数

文字ベクトル | string スカラー | 関数ハンドル

"x" 座標のパラメトリック関数。文字ベクトル、string スカラー、あるいは名前付き関数または無名関数の関数ハンドルとして指定します。

x = funx(u,v) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。

関数を文字ベクトルまたは string スカラーとして指定する場合、配列の乗算、除算、およびべき乗が常に暗黙的に指定されます。たとえば、x^2 は x.^2 と解釈されます。

例: 'u*sin(v)'

関数を関数ハンドルとして指定する場合に最高のパフォーマンスを得るには、行列演算子ではなく配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: @(u,v) u.*sin(v)

funy — y 座標のパラメトリック関数

文字ベクトル | string スカラー | 関数ハンドル

"y" 座標のパラメトリック関数。文字ベクトル、string スカラー、あるいは名前付き関数または無名関数の関数ハンドルとして指定します。

y = funy(u,v) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。

関数を文字ベクトルまたは string スカラーとして指定する場合、配列の乗算、除算、およびべき乗が常に暗黙的に指定されます。たとえば、x^2 は x.^2 と解釈されます。

例: '-u*cos(v)'

関数を関数ハンドルとして指定する場合に最高のパフォーマンスを得るには、行列演算子ではなく配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: @(u,v) -u.*cos(v)

funz — z 座標のパラメトリック関数

文字ベクトル | string スカラー | 関数ハンドル

"z" 座標のパラメトリック関数。文字ベクトル、string スカラー、あるいは名前付き関数または無名関数の関数ハンドルとして指定します。

z = funz(u,v) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。

関数を文字ベクトルまたは string スカラーとして指定する場合、配列の乗算、除算、およびべき乗が常に暗黙的に指定されます。たとえば、x^2 は x.^2 と解釈されます。

例: '-u*cos(v)'

関数を関数ハンドルとして指定する場合に最高のパフォーマンスを得るには、行列演算子ではなく配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: @(u,v) v

uvinterval — u および v のプロット区間

[-2π 2π -2π 2π] (既定値) | [min max] 形式のベクトル | [umin umax vmin vmax] 形式のベクトル

u および v のプロット区間。次のいずれかの形式で指定します。

• [min max] 形式のベクトル — u および v の両方に区間 [min max] を使用します。

• [umin umax vmin vmax] 形式のベクトル — u に区間 [umin umax]、v に区間 [vmin vmax] を使用します。

n — グリッドのサイズ

60 (既定値) | 正の整数

グリッドのサイズ。正の整数として指定します。グリッドは n 行 n 列の次元をもちます。

ax — axes オブジェクト

axes オブジェクト

axes オブジェクト。axes オブジェクトを指定しない場合、ezsurf は現在の座標軸を使用します。

拡張機能

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

ezsurf 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• この関数は GPU 配列を受け入れますが、GPU 上では実行されません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

使用上の注意および制限:

• この関数は分散配列に対して演算を行いますが、クライアントの MATLAB^® で実行されます。

詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

R2016a: ezsurf は非推奨

ezsurf は推奨されません。代わりに fsurf を使用してください。ezsurf を削除する予定はありません。

fsurf では、プロットする入力関数は関数ハンドルであることが求められます。ezsurf は、関数ハンドル、文字ベクトル、または string を受け入れます。次の表に、ezsurf のいくつかの一般的な使用方法と、代わりに fsurf を使用するようにコードを更新する方法を示します。

非推奨	推奨
ezsurf('real(atan(x+i*y))')	fsurf(@(x,y) real(atan(x+i*y)))
ezsurf('sin(x)+cos(y)')	fsurf(@(x,y) sin(x)+cos(y))
ezsurf(@(x,y) sqrt(x.^2+y.^2))	fsurf(@(x,y) sqrt(x.^2+y.^2))

参考

fcontour | fmesh | fplot | fplot3 | fsurf | surf

トピック

• 無名関数