divergence
ベクトル場の発散を計算
構文
説明
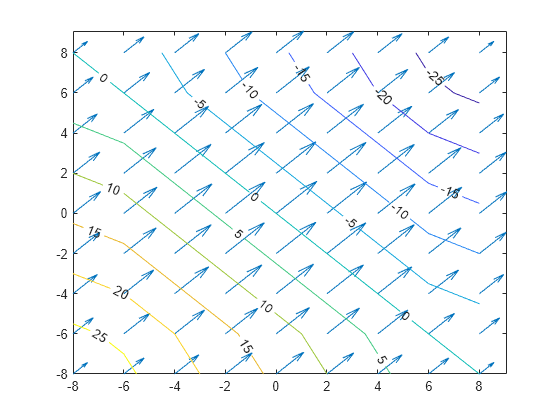
例
入力引数
詳細
アルゴリズム
divergence は、有限差分を使用してその定義で偏導関数を計算します。内部データ点の場合、偏導関数は "中心差分" を使用して計算されます。端のデータ点の場合、偏導関数は "片側 (前進) 差分" を使用して計算されます。
たとえば、位置が X と Y でサイズが m 行 n 列の行列 Fx と Fy で表される 2 次元ベクトル場 F について考えます。位置は [X,Y] = meshgrid(x,y) で作成された 2 次元グリッドです。ここで、x は長さ n のベクトル、y は長さ m のベクトルです。divergence は偏導関数 ∂Fx / ∂x と ∂Fy / ∂y を次のように計算します。
dFx(:,i) = (Fx(:,i+1) - Fx(:,i-1))/(x(i+1) - x(i-1))およびdFy(j,:) = (Fy(j+1,:) - Fy(j-1,:))/(y(j+1) - y(j-1))(内部データ点の場合)
dFx(:,1) = (Fx(:,2) - Fx(:,1))/(x(2) - x(1))およびdFx(:,n) = (Fx(:,n) - Fx(:,n-1))/(x(n) - x(n-1))(左端と右端のデータ点の場合)
dFy(1,:) = (Fy(2,:) - Fy(1,:))/(y(2) - y(1))およびdFy(m,:) = (Fy(m,:) - Fy(m-1,:))/(y(m) - y(m-1))(上端と下端のデータ点の場合)
ベクトル場の数値発散は div = dFx + dFy と等価です。
拡張機能
バージョン履歴
R2006a より前に導入