curl
ベクトル場の回転と角速度
構文
説明
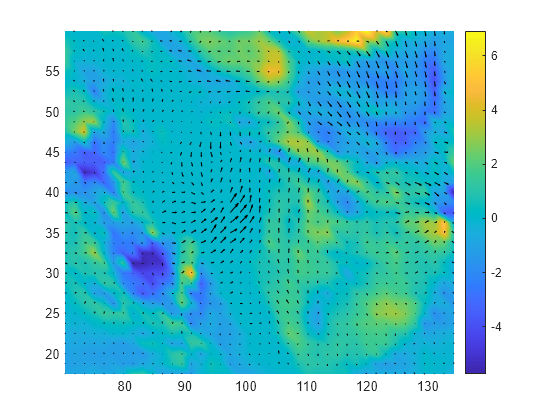
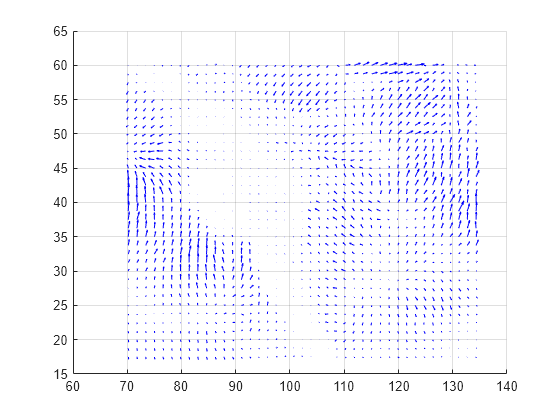
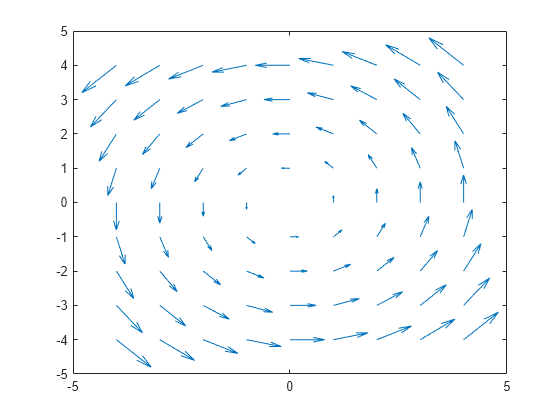
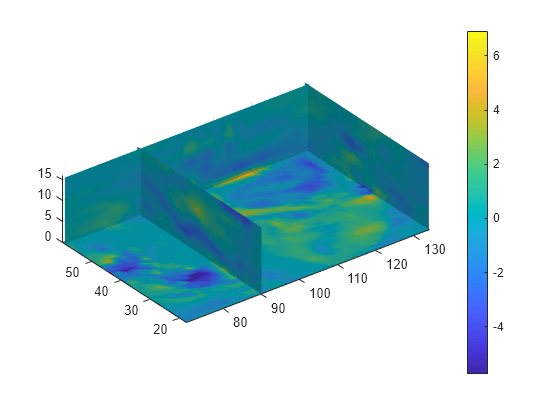
例
入力引数
出力引数
詳細
アルゴリズム
curl は、有限差分を使用してその定義で偏導関数を計算します。内部データ点の場合、偏導関数は "中心差分" を使用して計算されます。端のデータ点の場合、偏導関数は "片側 (前進) 差分" を使用して計算されます。
たとえば、位置が X と Y でサイズが m 行 n 列の行列 Fx と Fy で表される 2 次元ベクトル場 F について考えます。位置は [X,Y] = meshgrid(x,y) で作成された 2 次元グリッドです。ここで、x は長さ n のベクトル、y は長さ m のベクトルです。curl は偏導関数 ∂Fy / ∂x と ∂Fx / ∂y を次のように計算します。
dFy_dx(:,i) = (Fy(:,i+1) - Fy(:,i-1))/(x(i+1) - x(i-1))およびdFx_dy(j,:) = (Fx(j+1,:) - Fx(j-1,:))/(y(j+1) - y(j-1))(内部データ点の場合)
dFy_dx(:,1) = (Fy(:,2) - Fy(:,1))/(x(2) - x(1))およびdFy_dx(:,n) = (Fy(:,n) - Fy(:,n-1))/(x(n) - x(n-1))(左端と右端のデータ点の場合)
dFx_dy(1,:) = (Fx(2,:) - Fx(1,:))/(y(2) - y(1))およびdFx_dy(m,:) = (Fx(m,:) - Fx(m-1,:))/(y(m) - y(m-1))(上端と下端のデータ点の場合)
ベクトル場の数値回転は curlz = dFy_dx - dFx_dy と等しくなり、角速度は cav = 0.5*curlz です。
拡張機能
バージョン履歴
R2006a より前に導入