alphaShape
2 次元および 3 次元の点で構成される多角形および多面体
説明
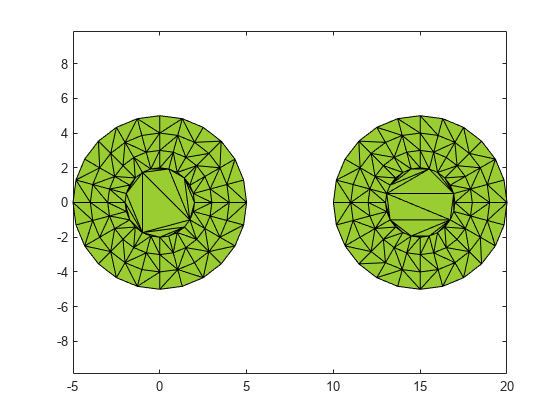
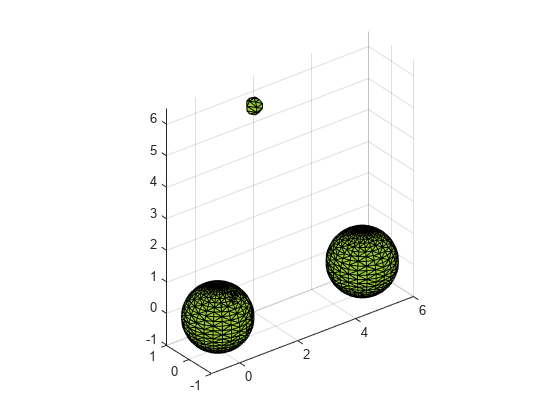
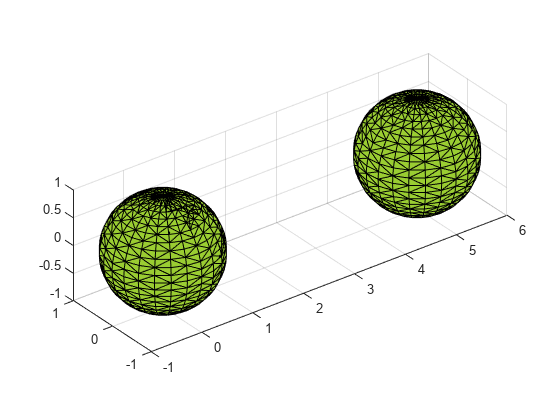
alphaShape は、2 次元または 3 次元の一連の点を囲む境界領域または境界ボリュームを作成します。alphaShape オブジェクトを操作して点にどれくらい厳密に近似させるかを調整することで、凹領域を作成できます。また、点の追加や削除、あるいは穴や領域の抑制もできます。
alphaShape オブジェクトの作成後、幾何学的なクエリを実行できます。たとえば、点が形状の内側にあるかどうかを確認したり、形状を構成する領域の数を求めたりできます。また、面積、周囲長、表面積、体積などの有用な数量を計算し、視覚的検証のために形状をプロットすることもできます。
作成
alphaShape オブジェクトを作成するには、形状の頂点を定義する入力引数をもつ関数 alphaShape を使用します。alphaShape の作成時に、アルファ半径および穴または領域のしきい値を指定することもできます。
構文
説明
shp = alphaShape(___,Name,Value)Name,Value のペアの引数によって指定された追加オプションを使用します。たとえば、'HoleThreshold' を使用して内部の穴や隙間を抑制できます。
入力引数
名前と値の引数
プロパティ
オブジェクト関数
alphaSpectrum | 独立したアルファ形状を生成するアルファ値 |
criticalAlpha | 形状の臨界遷移を定義するアルファ半径 |
numRegions | アルファ形状の領域の数 |
inShape | 点がアルファ形状の内側にあるかどうかを判定 |
alphaTriangulation | アルファ形状を塗りつぶす三角形分割 |
boundaryFacets | アルファ形状の境界の小平面 |
perimeter | 2 次元アルファ形状の周囲長 |
area | 2 次元アルファ形状の面積 |
surfaceArea | 3 次元アルファ形状の表面積 |
volume | 3 次元アルファ形状の体積 |
plot | アルファ形状のプロット |
nearestNeighbor | アルファ形状の最近傍の境界点を求める |
例
2 次元の点群データの形状を求めます。
2 次元の点の集合を作成してプロットします。
th = (pi/12:pi/12:2*pi)'; x1 = [reshape(cos(th)*(1:5), ... numel(cos(th)*(1:5)),1); 0]; y1 = [reshape(sin(th)*(1:5), ... numel(sin(th)*(1:5)),1); 0]; x = [x1;x1+15]; y = [y1;y1]; plot(x,y,".") axis equal
既定のアルファ半径を使用して点集合のアルファ形状を計算します。
shp = alphaShape(x,y); plot(shp)
既定のアルファ半径の値を確認します。
shp.Alpha
ans = 0.7752
既定のアルファ半径を使用した場合、アルファ形状の境界がギザギザになります。点集合の境界を明確にするために、アルファ半径の値を大きくします。
アルファ値を 2.5 にしてアルファ形状を計算します。
shp.Alpha = 2.5; plot(shp)
3 次元の点群データの形状を求めます。
3 次元の点の集合を作成してプロットします。
[x1,y1,z1] = sphere(24); x1 = x1(:); y1 = y1(:); z1 = z1(:); x2 = x1+5; P = [x1 y1 z1; x2 y1 z1]; P = unique(P,"rows"); plot3(P(:,1),P(:,2),P(:,3),".") axis equal grid on
アルファ半径を 1 にして 3 次元アルファ形状を計算します。
shp = alphaShape(P(:,1),P(:,2),P(:,3),1);
plot(shp)
axis equal
アルファ半径を指定してアルファ形状を作成し、アルファ形状内の穴を塗りつぶします。
2 次元の点の集合を作成してプロットします。
th = (pi/12:pi/12:2*pi)'; x1 = [reshape(cos(th)*(2:5), ... numel(cos(th)*(2:5)),1);]; y1 = [reshape(sin(th)*(2:5), ... numel(sin(th)*(2:5)),1);]; x = [x1;x1+15;]; y = [y1;y1]; plot(x,y,".") axis equal
アルファ半径を 1 にして点集合のアルファ形状を計算します。
shp = alphaShape(x,y,1); plot(shp)
アルファ半径を 1 にすると、穴を含む 2 つの領域で構成されるアルファ形状が生成されます。アルファ形状内の小さい穴を抑制するには、塗りつぶす最も大きい穴の面積を推定して HoleThreshold を指定します。形状に含まれるすべての穴を塗りつぶすには、任意に大きい値を HoleThreshold に代入します。
HoleThreshold を 15 に指定して、穴を抑制する新しいアルファ形状を作成します。
shp = alphaShape(x,y,1,HoleThreshold=15); plot(shp)
領域のしきい値を設定して、アルファ形状の領域数を制御します。
3 次元の点の集合を作成してプロットします。
[x1,y1,z1] = sphere(24);
x1 = x1(:);
y1 = y1(:);
z1 = z1(:);
x2 = x1 + 5;
[x3,y3,z3] = sphere(5);
x3 = x3(:) + 5;
y3 = y3(:);
z3 = z3(:) + 25;
P = [x1 y1 z1;
x2 y1 z1;
0.25*x3 0.25*y3 0.25*z3];
P = unique(P,"rows");
plot3(P(:,1),P(:,2),P(:,3),".")
axis equal
grid on
アルファ半径を 1 にして点集合のアルファ形状を計算します。
shp = alphaShape(P,1);
plot(shp)
axis equal
この場合、2 つの同じサイズの球面の上に小さい領域が生成されます。この領域を抑制するには、その体積を推定して RegionThreshold を指定します。
RegionThreshold を 2 に指定します。2 つの大きい領域だけを含む形状が生成されます。
shp.RegionThreshold = 2;
plot(shp)
axis equal
既存のアルファ形状に点を追加します。
2 次元の点の集合を作成してプロットします。
th = (pi/12:pi/12:2*pi)'; x1 = [reshape(cos(th)*(1:5), ... numel(cos(th)*(1:5)),1); 0]; y1 = [reshape(sin(th)*(1:5), ... numel(sin(th)*(1:5)),1); 0]; x = [x1;x1+15;]; y = [y1;y1]; plot(x,y,".") axis equal
アルファ半径を 1 にして点集合のアルファ形状を計算します。2 つの領域で構成されるアルファ形状が生成されます。
shp = alphaShape(x,y,1); plot(shp)
次に、新しい点を行列 shp.Points に直接追加して、アルファ形状に 3 つ目の領域を追加します。
x3 = x1 + 8; y3 = y1 + 10; shp.Points(end+1,:) = [x3 y3]; plot(shp)
交差する 2 つのリングを表す三角形分割を作成し、結果を STL ファイルに書き込みます。
1 つ目のリングを表すには、内径が 1 で外径が 5 のトーラス面を定義します。
R = 5;
r = 1;
angle = linspace(0,2*pi,50);
angle(end) = []; % Omit the repeated point for 0 and 2pi
[theta,omega] = meshgrid(angle,angle);トーラスを表す座標 "x"、"y"、"z" を定義します。
X = (R+r.*cos(theta)).*cos(omega); Y = (R+r.*cos(theta)).*sin(omega); Z = r.*sin(theta);
アルファ半径が 2 の alphaShape オブジェクトを作成します。
shp = alphaShape(X(:),Y(:),Z(:),2);
alphaShape の境界面から三角形分割を抽出します。この三角形分割は 1 つ目のリングを表します。
[tri,xyz] = shp.boundaryFacets; t1 = triangulation(tri,xyz);
三角形分割を回転させて 2 つ目のリングを定義します。
t2 = triangulation(tri,xyz*[1 0 0;0 0 1;0 1 0] + [4 0 0]);
2 つの三角形分割を結合します。
Points = [t1.Points;t2.Points];
Connectivity = ...
[t1.ConnectivityList;
t2.ConnectivityList + size(t1.Points,1)];
trCombined = triangulation(Connectivity,Points);結果の三角形分割をプロットします。
p = trisurf(trCombined); p.EdgeAlpha = 0.4;
三角形分割から STL ファイルを作成します。
stlwrite(trCombined,"Rings.stl");拡張機能
バージョン履歴
R2014b で導入
