領域境界のタイプ

凸包と非凸多角形の比較

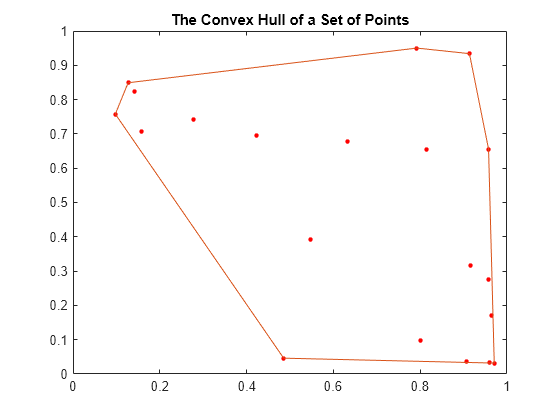
N 次元空間で、点集合の凸包は集合のすべての点で囲まれた最小の凸領域です。ペグ ボードのペグとして 2 次元の点集合を考える場合、集合の凸包はゴムバンドを使って作成され、それを使ってすべてのペグを囲みます。

rng('default')
x = rand(20,1);
y = rand(20,1);
plot(x,y,'r.','MarkerSize',10)
hold on
k = convhull(x,y);
plot(x(k),y(k))
title('The Convex Hull of a Set of Points')
hold off

凸多角形は、凹の頂点をもたない多角形です。たとえば以下のようになります。

x = rand(20,1);
y = rand(20,1);
k = convhull(x,y);
plot(x(k),y(k))
title('Convex Polygon')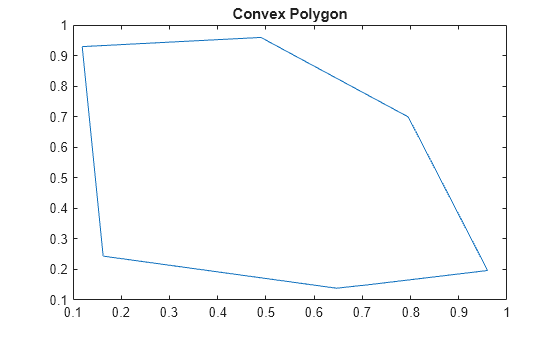

凸でない点集合の境界を作成することもできます。上記の凸包を縮めて絞め付けると、凹の頂点をもつ非凸多角形のすべての点を含めることができます。

k = boundary(x,y,0.9);
plot(x(k),y(k))
title('Nonconvex Polygon')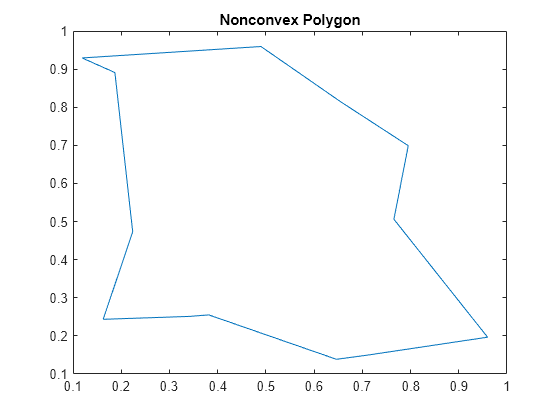

凸包は、多くの用途があります。集合の凸包から平面内に設定した離散点で指定される領域上の上限を計算することができます。凸包は、より複雑な多角形または多面体の表現を簡単にします。たとえば、2 つの凸でない本体が交差するかどうか確認するため、一連の高速の拒否ステップを適用して、完全交差の解析のペナルティを避けることができます。

• 各々の本体のまわりの軸の範囲の枠内が交差しているかどうか、確認します。

• 選択枠が交差している場合、各々の本体の凸包を計算し、包の交差をチェックすることができます。

凸包が交差していない場合、より多くの総合的な交差テストを回避することができます。

凸包と非凸多角形は比較的単純な境界を表す便利な方法ですが、これらは実際にはアルファ形状と呼ばれるより一般的な幾何構造の特定のインスタンスです。

アルファ形状

点集合のアルファ形状は、凸包の "一般化" および Delaunay 三角形分割の部分グラフです。つまり、凸包はアルファ形状の 1 つのタイプにすぎず、アルファ形状の全ファミリは指定された点集合の Delaunay 三角形分割から得ることができます。

rng(4)
x = rand(20,1);
y = rand(20,1);
plot(x,y,'r.','MarkerSize',20)
hold on
shp = alphaShape(x,y,100);
plot(shp)
title('Convex Alpha Shape')
hold off

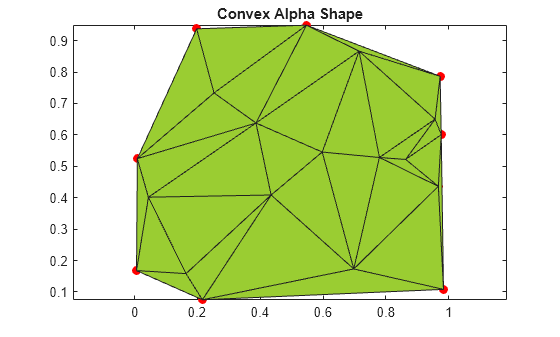
凸包とは異なり、アルファ形状は詳細レベル、つまり点集合の境界にどれだけ厳密に近似するかを制御するパラメーターがあります。このパラメーターは "アルファ" または "アルファ半径" と呼ばれます。アルファ半径を 0 から Inf に変化させることで、その点集合に固有の一連のアルファ形状が得られます。

plot(x,y,'r.','MarkerSize',20)
hold on
shp = alphaShape(x,y,.5);
plot(shp)
title('Nonconvex Alpha Shape')
hold off

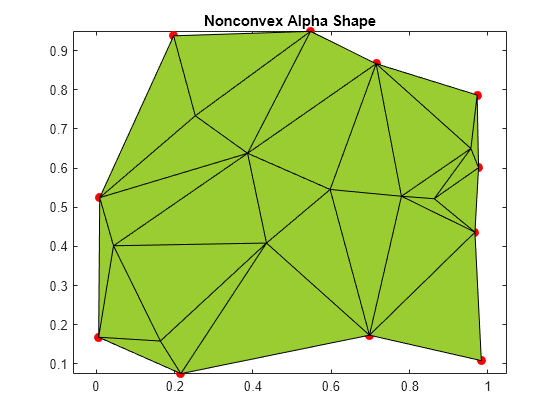
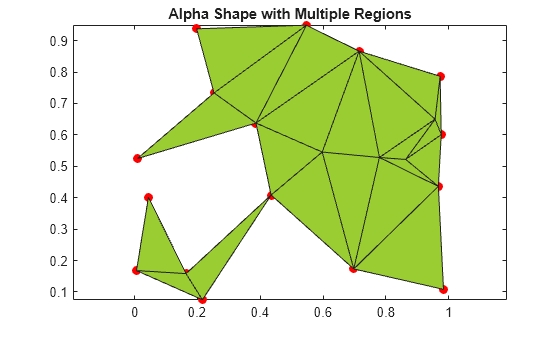
アルファ半径を変化させると、複数の領域をもつアルファ形状が得られることがあります。これには、穴がある場合もない場合もあります。ただし、MATLAB® の関数 alphaShape は常に正規化されたアルファ形状を返すため、孤立した、接続されていない点、エッジ、面の発生は防がれます。

plot(x,y,'r.','MarkerSize',20)
hold on
shp = alphaShape(x,y);
plot(shp)
title('Alpha Shape with Multiple Regions')
hold off

参考

convhull | alphaShape

関連するトピック

• delaunayTriangulation クラスの使用
• 三角形分割の行列形式