Main Content

このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

プロセス モデルの推定

ライブ エディターで時間または周波数領域の単入力単出力 (SISO) システムの連続時間プロセス モデルを推定する

R2019b 以降

このページをすべて展開する

説明

[プロセス モデルの推定] タスクでは、SISO システムのプロセス モデルを対話的に推定および検証できます。モデル構造を定義および変更し、初期状態の処理や探索方法などのオプションのパラメーターを指定できます。このタスクは、ライブ スクリプト用の MATLAB® コードを自動生成します。ライブ エディター タスク全般の詳細については、ライブ スクリプトへの対話型タスクの追加を参照してください。

プロセス モデルは、線形システム ダイナミクスを記述した単純な連続時間伝達関数です。プロセス モデルの要素には、静的ゲイン、時定数、時間遅延、積分器、プロセス ゼロなどがあります。

プロセス モデルは、多くの産業でシステム ダイナミクスを記述するためによく使用されており、さまざまな量産環境に適用できます。このモデルの利点は、シンプルであること、伝達遅延の推定をサポートすること、モデル係数が極と零点として簡単に解釈できることです。プロセス モデルの推定の詳細については、What Is a Process Model?を参照してください。

[プロセス モデルの推定] タスクは、より一般的な System Identification アプリから独立しています。複数のモデル構造の推定を計算して比較する場合は、System Identification アプリを使用します。

開始するには、入出力データが含まれている実験データを MATLAB ワークスペースに読み込んでから、データをタスクにインポートします。次に、推定するモデル構造を選択します。タスクでは、さまざまなモデル構造で実験して測定に対する各モデルの出力の適合度を比較できるようにするコントロールとプロットが用意されています。

関連する関数

[プロセス モデルの推定] で生成されるコードは以下の関数を使用します。

このタスクでは idproc プロセス モデルが推定されます。

Estimate Process Model task in Live Editor

タスクを開く

MATLAB エディターでライブ スクリプトに [プロセス モデルの推定] タスクを追加するには、次を行います。

  • [ライブ エディター] タブで、[タスク]、[プロセス モデルの推定] を選択します。

  • スクリプトのコード ブロック内で、process、estimate などの関連するキーワードを入力します。コマンドの補完候補から [プロセス モデルの推定] を選択します。

例

すべて展開する

ライブ スクリプトを開く

[プロセス モデルの推定] ライブ エディター タスクを使用して、プロセス モデルを推定し、モデル出力を測定データと比較します。

データの設定

測定データ tt1 を MATLAB ワークスペースに読み込みます。tt1 は 1 つの入力変数 u と 1 つの出力変数 y を含む timetable です。

load sdata1 tt1

タスクへのデータのインポート

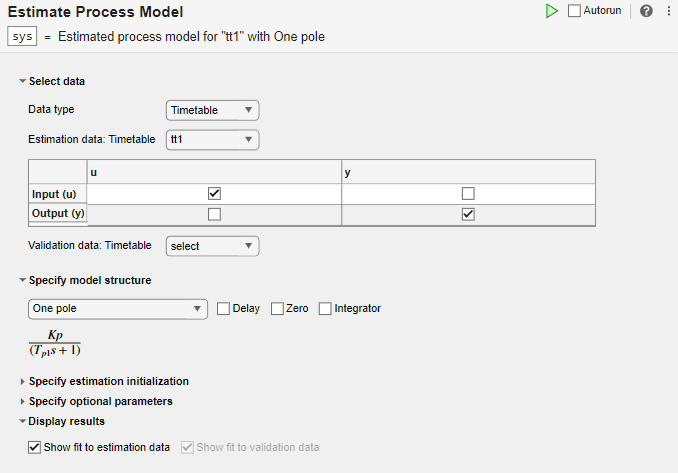
[データの選択] セクションで [データ型] を Timetable に設定し、[推定データ: オブジェクト] を tt に設定します。

タスクで、tt1 の入出力変数名が含まれた表が表示されます。

既定の設定を使用したモデルの推定

モデル構造およびオプション パラメーターを調べます。

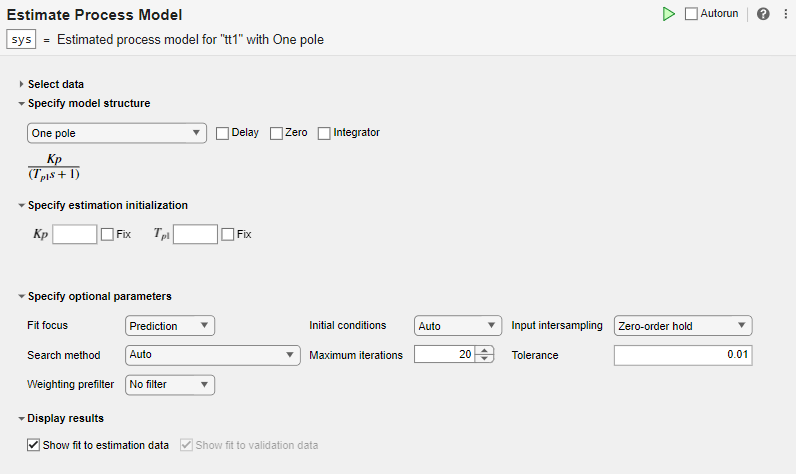
[モデル構造の指定] セクションの既定のオプションは One Pole であり、遅延も、零点も、積分器も指定されていません。このセクションのパラメーターの下にある方程式で、指定した構造が表示されます。

[推定の初期化の指定] セクションで、モデル構造のパラメーターに一致する初期化パラメーターにより、推定の開始点を設定できます。[固定] を選択すると、パラメーターは指定した値に固定されたままになります。この例では、初期化を指定しません。この場合、タスクでは開始点に既定値を使用します。

[オプション パラメーターの指定] セクションでは、プロセス推定の既定のオプションが設定されています。

緑の矢印をクリックして、[ライブ エディター] タブからタスクを実行します。[自動実行] を選択して、パラメーターを更新するごとにタスクを自動的に実行することもできます。

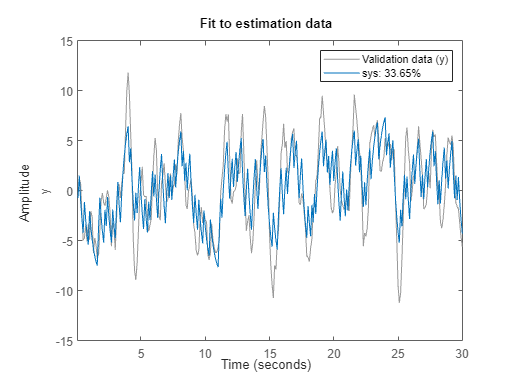
プロットで推定データ、推定モデル出力、および適合率 (%) が表示されます。

パラメーター設定の実験

パラメーター設定を実験し、適合への影響を確認します。

たとえば、One Pole 構造に遅延を追加してタスクを実行します。

推定の適合度が向上しましたが、適合率はそれでも 50% 未満です。

別のモデル構造を試します。[モデル構造の指定] で遅延を指定せずに Underdamped Pair を選択し、タスクを実行します。

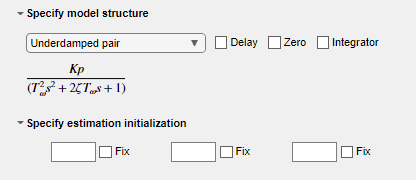
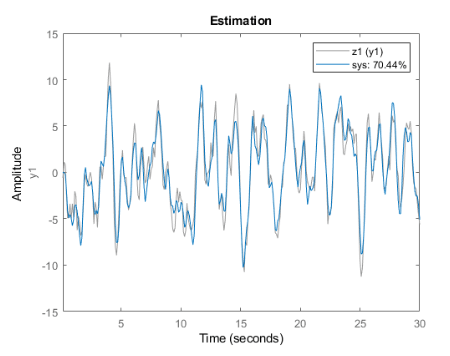
適合結果が大幅に向上します。

コードの生成

タスクで生成されたコードを表示するには、パラメーター セクションの下部にある をクリックします。表示されたコードには、タスクの現在のパラメーター構成が反映されています。

ライブ スクリプトを開く

別個の推定データと検証データを使用して、推定プロセス モデルを検証できるようにします。

データの設定

測定データ iddata1 を MATLAB ワークスペースに読み込み、その内容を調べます。

load sdata1 umat1 ymat1 Ts

データを 2 セットに分割します。半分は推定用、もう半分は検証用です。元のデータ セットには 300 個のサンプルが含まれているため、新しい各データ セットには 150 個のサンプルが含まれています。

u_est = umat1(1:150);
u_val = umat1(151:300);
y_est = ymat1(1:150);
y_val = ymat1(151:300);
Ts
Ts = 0.1000

タスクへのデータのインポート

[データの選択] セクションで、[データ型] を [数値] に設定します。[サンプル時間] を 0.1 秒 (0.1 秒) に設定します。推定と検証に適切なデータ セットを選択します。

モデルの推定と検証

ライブ エディター タスクでのプロセス モデルの推定の例では、モデル構造 Underdamped Pair を使用して最良の結果を得ています。この例でも同じオプションを選択します。

タスクを実行します。タスクを実行すると 2 つのプロットが作成されます。最初のプロットには推定結果が表示され、2 番目のプロットには検証結果が表示されます。

推定データへの適合はライブ エディター タスクでのプロセス モデルの推定より若干悪くなっています。現在の例の推定では、モデルの推定に使用しているデータが半分だけです。検証データへの適合は、より一般的にモデルの良好さを表します。この検証データへの適合が、推定データへの適合より良い結果になっています。

パラメーター

すべて展開する

データの選択

このタスクでは、等間隔の時間でサンプリングされた数値測定値が受け入れられます。入力信号と出力信号には複数のチャネルを含めることができます。データは、数値配列として (Numeric または Frequency の場合)、timetable として、またはデータ オブジェクト (iddata オブジェクトや idfrd オブジェクトなど) に入れてパッケージ化できます。複数実験データの場合、数値データおよび timetable データは cell 配列としてパッケージ化できます。timetable の cell 配列の場合、すべての timetable に同じ変数名が含まれている必要があります。データ オブジェクトは、複数実験データを内部的に処理します。

選択したデータ型により、追加パラメーターを指定する必要があるかどうかが決まります。

  • 数値 — 選択した時間単位で [サンプル時間] および [開始時間] を指定します。

  • timetable — timetable にはサンプル時間および開始時間に関する情報が既に含まれているため、追加パラメーターは指定しません。

  • 周波数 — MATLAB ワークスペースで周波数ベクトルの変数名を選択して [周波数] を指定します。周波数ベクトルの単位を指定します。[サンプル時間] (秒単位) を指定します。

  • データ オブジェクト — データ オブジェクトには時間または周波数サンプリングに関する情報が既に含まれているため、追加パラメーターは指定しません。

MATLAB ワークスペースの選択肢から入出力変数名を選択します。これらのパラメーターは [データ型] が [数値] または [周波数] の場合に使用します。

検証データの指定はオプションですが、推奨されます。

MATLAB ワークスペースの選択肢から timetable 変数名を選択します。このパラメーターは [データ型] が [timetable] の場合に使用します。タスクで、入力と出力用の timetable 変数名が表示されます。推定と検証用の timetable には同じ変数名が含まれている必要があります。

MATLAB ワークスペースの選択肢からデータ オブジェクト変数名を選択します。このパラメーターは [データ型] が [データ オブジェクト] の場合に使用します。

モデル構造の指定

このタスクでは、4 つの基本構造の 1 つを指定できます。これらの構造は、単純な 1 次プロセスから、複素共役 (不足減衰) の極をもつ動的な 2 次または 3 次プロセスまでさまざまです。

  • 1 つの極

  • 2 つの実極

  • 不足減衰ペア

  • 不足減衰ペア + 実極

1 つのサンプルの伝達遅延 (入力から出力への遅延) を含めます。伝達遅延はむだ時間とも呼ばれます。

分子にプロセス ゼロを含めます。

積分器を含めます。追加の 1/ s 項で表されます。積分器を含めると、自己制御プロセスが作成されます。

推定の初期化の指定

推定の初期値、およびその値を固定するのか推定するのかを指定します。指定する値は、モデル構造および [遅延] と [ゼロ] の仕様によって異なります。タスクでは [モデル構造の指定] の下に、指定したシステムを表す方程式が表示されます。この方程式には、推定できるすべてのパラメーターおよび初期化または固定できるすべてのパラメーターが含まれています。可能なパラメーターは次のとおりです。

  • Kp — 静的ゲイン

  • Tp1 — 最初の実極の時定数

  • Tp2 — 2 番目の実極の時定数

  • Tω — 固有振動数の逆数に等しい、複素数の極の時定数

  • ζ — 複素数の極の減衰係数

  • Td — 伝達遅延

  • Tz — プロセス ゼロの時定数

すべての時間ベースのパラメーターは、[サンプル時間] で選択した時間単位になります。

オプション パラメーターの指定

適合フォーカスでは、推定時に損失関数で最小化する誤差を指定します。

  • 予測 — 測定出力と予測出力間の 1 ステップ先の予測誤差を最小化します。この推定法では、推定入出力用に良好な予測子モデルを生成することに焦点を合わせます。[予測] フォーカスでは通常、最良の推定結果が得られます。これは、入力と出力の両方の測定値を使用するので、外乱が考慮されるためです。

  • シミュレーション — 測定出力とシミュレーション出力間の誤差を最小化します。この推定法では、推定入出力に良好に適合する、シミュレートされたモデルの応答を生成することに焦点を合わせます。[シミュレーション] フォーカスは通常、(特に元の推定に使用されていないデータ セットを使用した) 検証に最適です。

モデルを初期化する特定の手法を選択する場合は、このオプションを設定します。既定の設定 [自動] では、推定データに基づいて手法が選択されます。選択肢は以下のとおりです。

  • ゼロ — 初期状態が 0 に設定されます。

  • 推定 — 初期状態が、独立した推定パラメーターとして扱われます。

  • バックキャスト — 初期状態は、最小二乗近似を使用して推定されます。

入力インターサンプリングは入力データのプロパティです。このタスクでは、プロセス モデルの推定時にこのプロパティを使用します。データ型が [時間] または [周波数] の場合に [入力インターサンプリング] を指定します。iddata オブジェクトを使用している場合、オブジェクトにはインターサンプリング情報が既に含まれています。このプロパティの選択肢は次のとおりです。

  • ゼロ次ホールド — サンプル間で区分的に一定な入力信号

  • 三角形近似 — サンプル間の区分的に線形な入力信号 (1 次ホールドとも呼ばれる)

  • 帯域制限 — ナイキスト周波数を超えると入力信号のパワーがゼロになる

  • 自動 — 反復ごとに、推定コストの削減につながる最初の方向の降下が見つかるまで手法を順に試します。

  • ガウス・ニュートン法 — 部分空間のガウス・ニュートン法による最小二乗法の探索。

  • レーベンバーグ・マルカート法 — レーベンバーグ・マルカート法による最小二乗法の探索。

  • 適応ガウス・ニュートン法 — 部分空間の適応ガウス・ニュートン法による探索。

  • 勾配探索 — 最急降下法による最小二乗法の探索。

誤差最小化時の最大反復回数を設定します。反復は、[最大反復回数] に達するか、[許容誤差] などの別の停止基準が満たされると停止します。

期待改善量が [許容誤差] より小さい場合、反復は停止します。

モデルの推定時にタスクで最小化する損失関数に重みプレフィルターを適用する場合にこのオプションを設定します。オプションを選択した場合は、ワークスペースでフィルター情報を含む関連する変数を選択する必要もあります。使用可能なオプションは、データの領域によって異なります。

重みプレフィルターデータの領域フィルター情報
フィルターなし時間と周波数 
通過帯域時間と周波数通過帯域。1 行 2 列の行ベクトルまたは n 行 2 列の行列として指定します。ここで、n は通過帯域の数です。
LTI フィルター時間と周波数SISO LTI モデル
周波数重みベクトル周波数周波数の重み。周波数ベクトルと同じ長さの列ベクトルとして指定します。

たとえば、SISO 周波数領域データを使用して推定を実行し、MATLAB ワークスペースに、プレフィルター用の周波数の重みが含まれている列ベクトル W があるものとします。タスクで、[重みプレフィルター]、[周波数重みベクトル] を選択し、変数 [W] を選択します。

結果の可視化

モデル出力と元の測定データの比較をプロットし、適合率 (%) も示します。別個の検証データがある場合は、2 番目のプロットで、検証入力データへのモデル応答が、検証データ セットからの測定出力と比較されます。

バージョン履歴

R2019b で導入

すべて展開する

参考

| | | | | | | (Control System Toolbox)