このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

c2d

連続時間から離散時間へモデルを変換

構文

sysd = c2d(sysc,Ts)

sysd = c2d(sysc,Ts,method)

sysd = c2d(sysc,Ts,opts)

[sysd,G] = c2d(___)

説明

sysd = c2d(sysc,Ts) は、入力でのゼロ次ホールドとサンプル時間 Ts を使用して、連続時間動的システム モデル sysc を離散化します。

sysd = c2d(sysc,Ts,method) は、離散化手法を指定します。

sysd = c2d(sysc,Ts,opts) は、離散化に対する追加オプションを指定します。

[sysd,G] = c2d(___) (sysc は、状態空間モデル) は、状態空間モデルの連続初期条件 x₀ と u₀ を離散時間初期状態ベクトル x[0]. にマッピングする行列 G を返します。

例

伝達関数の離散化

次の連続時間の伝達関数を離散化します。

$$H\left(s\right)=e^{-0.3s}\frac{s-1}{s^2+4s+5}.$$

このシステムには 0.3 秒の入力遅延があります。サンプル時間 Ts = 0.1 s での三角形 (1 次ホールド) 近似を使用してシステムを離散化します。

H = tf([1 -1],[1 4 5],'InputDelay', 0.3); 
Hd = c2d(H,0.1,'foh');

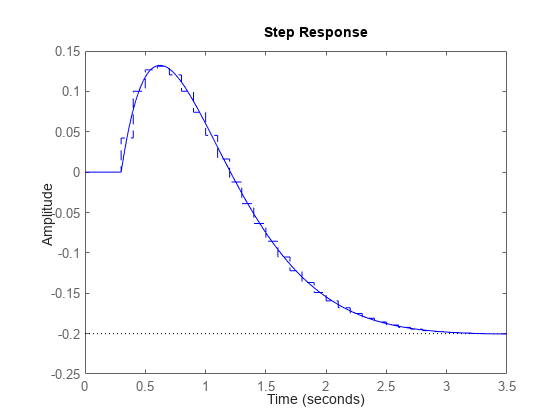
連続時間システムと離散化システムのステップ応答を比較します。

step(H,'-',Hd,'--')

係数に吸収された非整数遅延をもつモデルの離散化

入力のゼロ次ホールドと 10 Hz のサンプリング レートを使用して、次の遅延伝達関数を離散化します。

$$H\left(s\right)=e^{-0.25s}\frac{10}{s^2+3s+10}.$$

h = tf(10,[1 3 10],'IODelay',0.25); 
hd = c2d(h,0.1)

hd =
 
           0.01187 z^2 + 0.06408 z + 0.009721
  z^(-3) * ----------------------------------
                 z^2 - 1.655 z + 0.7408
 
Sample time: 0.1 seconds
Discrete-time transfer function.

この例では、離散化されたモデル hd に 3 サンプリング周期の遅延があります。離散化アルゴリズムは、残る半周期の遅延を hd の係数に吸収します。

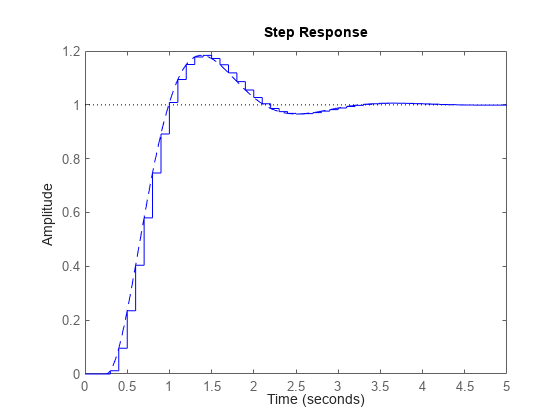
連続時間モデルと離散化モデルのステップ応答を比較します。

step(h,'--',hd,'-')

近似された非整数遅延をもつモデルの離散化

R2024a 以降

2 つの状態と 1 つの入力遅延をもつ連続時間状態空間モデルを作成します。

sys = ss(tf([1,2],[1,4,2]));
sys.InputDelay = 2.7

sys =
 
  A = 
       x1  x2
   x1  -4  -2
   x2   1   0
 
  B = 
       u1
   x1   2
   x2   0
 
  C = 
        x1   x2
   y1  0.5    1
 
  D = 
       u1
   y1   0
 
  Input delays (seconds): 2.7 
 
Continuous-time state-space model.

Tustin 離散化手法と Thiran フィルターを使用してモデルを離散化し、非整数遅延をモデル化します。サンプル時間 Ts は 1 秒です。

opt = c2dOptions('Method','tustin','ThiranOrder',3);
sysd1 = c2d(sys,1,opt)

sysd1 =
 
  A = 
            x1       x2
   x1  -0.4286  -0.5714
   x2   0.2857   0.7143
 
  B = 
           u1
   x1  0.5714
   x2  0.2857
 
  C = 
           x1      x2
   y1  0.2857  0.7143
 
  D = 
           u1
   y1  0.2857
 
  (values computed with all internal delays set to zero)

  Internal delays (sampling periods): 1  1  1 
 
Sample time: 1 seconds
Discrete-time state-space model.

既定では、離散化されたモデルにおいて、関数は追加の遅延を内部遅延としてモデル化します。離散化されたモデルで追加の遅延を状態としてモデル化するには、c2dOptions の DelayModeling オプションを 'state' に設定します。

opt2 = c2dOptions('Method','tustin','ThiranOrder',3,'DelayModeling','state');
sysd2 = c2d(sys,1,opt2)

sysd2 =
 
  A = 
              x1         x2         x3         x4         x5
   x1    -0.4286    -0.5714   -0.00265    0.06954      2.286
   x2     0.2857     0.7143  -0.001325    0.03477      1.143
   x3          0          0    -0.2432     0.1449    -0.1153
   x4          0          0       0.25          0          0
   x5          0          0          0      0.125          0
 
  B = 
             u1
   x1  0.002058
   x2  0.001029
   x3         8
   x4         0
   x5         0
 
  C = 
              x1         x2         x3         x4         x5
   y1     0.2857     0.7143  -0.001325    0.03477      1.143
 
  D = 
             u1
   y1  0.001029
 
Sample time: 1 seconds
Discrete-time state-space model.

これにより、離散化されたモデルは、3 次 Thiran フィルターに対応する 3 つの追加状態 x3、x4、x5 を含むようになります。むだ時間をサンプル時間で除算すると 2.7 となるので、3 次 Thiran フィルター ('ThiranOrder' = 3) はむだ時間全体を近似できます。

同定されたモデルの離散化

連続時間伝達関数を推定し、離散化します。

load iddata1
sys1c = tfest(z1,2);
sys1d = c2d(sys1c,0.1,'zoh');

2 次離散時間伝達関数を推定します。

sys2d = tfest(z1,2,'Ts',0.1);

離散化された連続時間の伝達関数モデル sys1d の応答と、直接推定した離散時間モデル sys2d を比較します。

compare(z1,sys1d,sys2d)

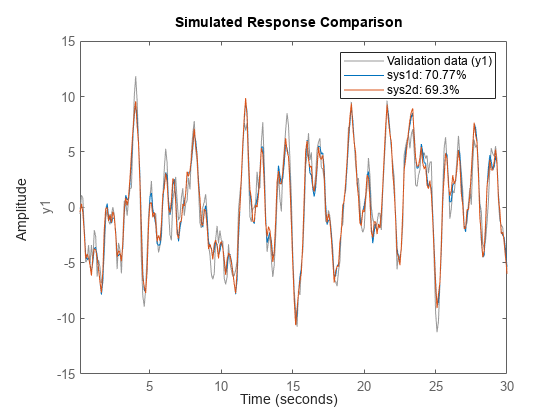
この 2 つのシステムはほぼ同じです。

予測子モデルの作成

同定された状態空間モデルを離散化して、応答の 1 ステップ先の予測子を構築します。

推定データを使用して、連続時間で同定された状態空間モデルを作成します。

load iddata2
sysc = ssest(z2,4);

sysc の 1 ステップ先の予測応答を予測します。

predict(sysc,z2)

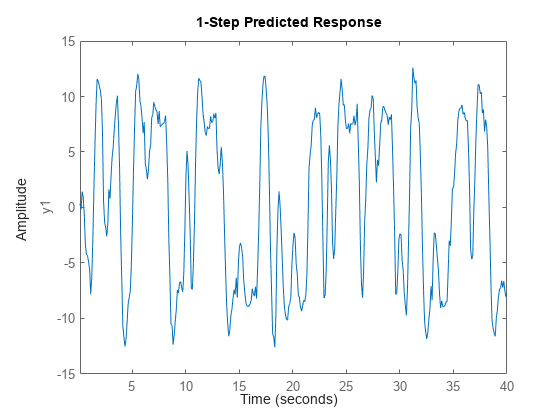
モデルを離散化します。

sysd = c2d(sysc,0.1,'zoh');

離散化モデル sysd から予測子モデルを作成します。

[A,B,C,D,K] = idssdata(sysd);
Predictor = ss(A-K*C,[K B-K*D],C,[0 D],0.1);

Predictor は測定した出力信号と入力信号 ([z1.y z1.u]) を使用して、sysc の 1 ステップ先を予測した応答を計算する 2 入力モデルです。

予測子モデルをシミュレートし、predict コマンドと同じ応答を得ます。

lsim(Predictor,[z2.y,z2.u])

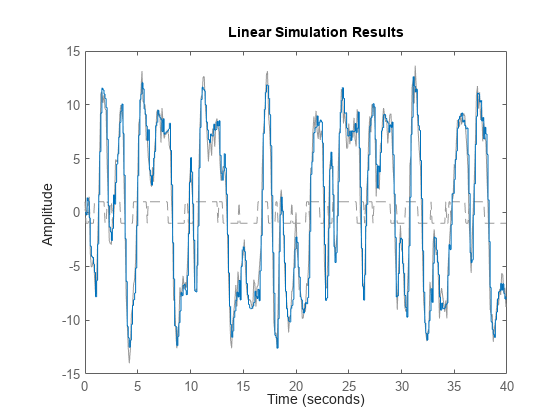
予測子モデルのシミュレーションの応答は、predict(sysc,z2) と同じになります。

入力引数

sysc — 連続時間動的システム

動的システム モデル

idtf、idss、idpolyなどの動的システム モデルとして指定される連続時間モデル。sysc は、周波数応答データ モデルにすることができません。'matched' 離散化手法が SISO システムのみをサポートする点を除き、sysc は、SISO または MIMO にすることができます。

sysc は、入出力遅延または内部遅延をもつことができますが、'matched'、'impulse' および 'least-squares' メソッドは内部遅延をもつ状態空間モデルをサポートしていません。

次の同定された線形システムは直接離散化できません。

• FunctionType が 'c' である idgrey モデル。最初に idss モデルに変換します。

• idproc モデル。最初に idtf または idpoly モデルに変換します。

Ts — サンプル時間

正のスカラー

サンプル時間。結果の離散時間システムのサンプリング周期を表す正のスカラーとして指定します。Ts は、sysc.TimeUnit プロパティである TimeUnit で表されます。

method — 離散化手法

'zoh' (既定値) | 'foh' | 'impulse' | 'tustin' | 'matched' | 'least-squares' | 'damped'

離散化手法。次の値のいずれかとして指定します。

• 'zoh' - ゼロ次ホールド (既定) 。サンプル時間 Ts の間、制御入力は区分的に一定であると仮定します。

• 'foh' - 三角形近似 (修正された 1 次ホールド。サンプル時間 Ts の間、制御入力は区分的に線形であると仮定します。

• 'impulse' — インパルス不変法による離散化

• 'tustin' — 双一次 (Tustin) メソッド。周波数プリワーピング (以前に 'prewarp' メソッドと呼ばれていたもの) によるこのメソッドを指定するには、c2dOptions の PrewarpFrequency オプションを使用します。

• 'matched' — 極-零点マッチング法

• 'least-squares' — 最小二乗法

• 'damped' — TRBDF2 式に基づく減衰 Tustin 近似 (sparss モデルのみ)。

各変換法のアルゴリズムの詳細については、連続/離散の変換方法を参照してください。

opts — 離散化オプション

c2dOptions オブジェクト

離散化オプション。c2dOptions オブジェクトとして指定します。たとえば、プリワープ周波数、Thiran フィルターの次数、または離散化手法をオプションとして指定します。

出力引数

sysd — 離散時間モデル

動的システム モデル

離散時間モデル。入力システム sysc と同じタイプの動的システム モデルとして返されます。

sysc が同定された (IDLTI) モデルの場合、sysd は次のようになります。

• sysc の測定成分とノイズ成分の両方を含みます。連続時間同定モデル sysc のイノベーション分散 λ はその NoiseVariance プロパティに格納され、ノイズ スペクトルのスペクトル密度の強度と解釈されます。このため、sysd のノイズ分散は λ/Ts になります。

• sysc の推定されたパラメーターの共分散は含みません。モデルの離散化中に共分散を変換する場合は、translatecov を使用します。

G — 状態空間モデルの連続初期条件の離散時間初期状態ベクトルへのマッピング

行列

状態空間モデル sysc の連続時間初期条件 x₀ および u₀ の離散時間初期状態ベクトル x[0] へのマッピング。行列として返されます。初期条件の初期状態ベクトルへのマッピングは次のとおりです。

$$x\left[0\right]=G\cdot \left[\begin{array}{c}{x}_0\\ u_0\end{array}\right]$$

むだ時間をもつ状態空間モデルの場合、むだ時間の離散化によって生じた追加の状態を考慮して、c2d は行列 G をゼロでパディングします。離散化システムにおけるむだ時間のモデル化については、連続/離散の変換方法を参照してください。

バージョン履歴

R2006a より前に導入

R2024a: 変換時に余分な状態の追加なし

c2d コマンドで、余分な遅延をモデル化するときに余分な状態が追加されなくなりました。既定では、c2d で内部遅延が使用されるようになり、同じ数の状態を含む離散化されたモデルが返されます。これにより、予測動作の精度が向上し、連続時間から離散時間への初期状態のマッピングが簡略化されます。

R2024a より前の従来の動作に戻すには、c2dOptions を使用してオプション セットを作成し、DelayModeling を "state" に設定します。

R2024a: mechss モデルのサポート

双一次 Tustin 近似法を使用して mechss モデルを離散化できるようになりました。mechss モデルの場合、'tustin' メソッドは Tustin 離散化の 2 次形式を計算します。これは、mechss モデルと同等の 1 次 sparss に Tustin を適用することと等価です。

R2024a: オフセットをもつモデルのサポートとその他の改善点

グリッド付きの線形パラメーター変動モデルなどのオフセットをもつモデルを c2d を使用して離散化できるようになりました。

さらに、c2dOptions で 2 つの新しいオプションが提供されます。

• DelayModeling — 余分な遅延を内部遅延 (既定) と追加状態のいずれとしてモデル化するかを指定します。

• Consistency — 状態空間配列における状態と遅延の一貫性を強制します。このオプションは、グリッド付きの LTV モデルまたは LPV モデルを離散化する場合に便利です。

参考

c2dOptions | d2c | d2d | thiran (Control System Toolbox) | translatecov

トピック

• 動的システム モデル
• Transforming Between Discrete-Time and Continuous-Time Representations
• 連続/離散の変換方法