このページは機械翻訳を使用して翻訳されました。元の英語を参照するには、ここをクリックします。

大域的最適化とは

大域的最適解と局所的最適解

最適化とは、関数を最小化する点を見つけるプロセスです。具体的には、

• 関数の 局所的 最小値とは、関数の値が近くの点の値以下であるが、遠い点よりも大きくなる可能性がある点です。

• 大域的最小値とは、関数の値が他のすべての実行可能点の値より小さいか等しい点です。

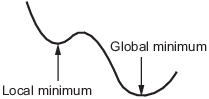
一般的に、Optimization Toolbox™ ソルバーは局所的最適値を見つけます。(この局所的最適値は、大域的最適値になることがあります。)彼らは出発点の引き込み領域内で最適値を見つけます。詳細については、引き込み領域を参照してください。

対照的に、Global Optimization Toolbox ソルバーは、複数の引き込み領域を探索するように設計されています。さまざまな方法で探索します。

• GlobalSearch と MultiStart は、いくつかの開始点を生成します。次に、ローカル ソルバーを使用して、開始点の引き込み領域内で最適値を見つけます。

• ga は、一連の開始点 (母集団と呼ばれる) を使用し、母集団からより良い点を繰り返し生成します。初期の母集団が複数の領域をカバーしている限り、ga は複数の領域を調査できます。

• particleswarm は、ga と同様に、一連の開始点を使用します。particleswarm は、母集団が多様であるため、一度に複数の領域を調べることができます。

• simulannealbnd はランダム探索を実行します。一般的に、simulannealbnd は、前の点よりも良い点であればそれを受け入れます。simulannealbnd は、別の領域に到達するために、時々悪い点を受け入れます。

• patternsearch は、隣接する点をいくつか調べてから、そのうちの 1 つを受け入れます。いくつかの隣接点が異なる領域に属している場合、patternsearch は本質的に一度に複数の領域を調べます。

• surrogateopt は、境界内で準ランダム サンプリングを開始し、目的関数の値が小さいものを探します。surrogateopt は、評価点から遠い点を優先する メリット関数 を使用し、大域解に到達しようとします。現在の点を改善できない場合、surrogateopt はリセットされ、境界内で再び広範囲にサンプリングが行われます。リセットは、surrogateopt が大域解を探索するもう 1 つの方法です。

引き込み領域

目的関数 f(x) が滑らかな場合、ベクトル –∇f(x) は f(x) が最も急激に減少する方向を示します。最急降下の式は以下のようになります。

$$\frac{d}{dt}x(t)=-\nabla f(x(t)),$$

t が大きくなるにつれて局所的最小値に向かうパス x(t) が生成されます。一般的に、互いに近い初期値 x(0) は、同じ最小点に向かう最も急な降下経路を示します。最急降下法の引き込み領域は、同じ局所的最小値に至る初期値の集合です。

次の図は、2 つの 1 次元の最小値を示しています。この図は、さまざまな線のスタイルでさまざまな引き込み領域を示し、最も急な降下の方向を矢印で示しています。この図と次の図の黒い点は、局所的最小値を示します。点 x(0) で始まる最急降下経路は、x(0) を含む引き込み領域の黒い点に向かいます。

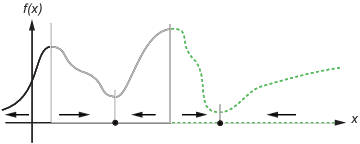
次の図は、最急降下経路が次元数が増えるにつれてどのように複雑になるかを示しています。

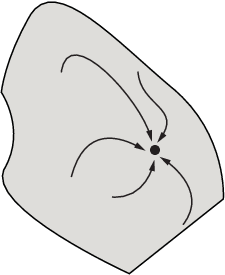
次の図は、さらに複雑な経路と引き込み領域を示しています。

制約は 1 つの引き込み領域をいくつかの断片に分割することがあります。たとえば、y の最小化を考えてみましょう。

• y ≥ |x|

• y ≥ 5 – 4(x–2)².

この図は、最終点を持つ 2 つの引き込み領域を示しています。

 図を生成するコード

myabs = @(x) abs(x);
mycurve = @(x) 5 - 4.*(x-2).^2;
myline = @(x) max(myabs(x),mycurve(x));
mybrdr = @(x) 1 + heaviside(x-2);
myarea = @(x,y) heaviside(y - myline(x)).*mybrdr(x);
% myarea = 0 where infeasible, 1 when x < 2, 2 when x > 2
marinv = @(x,y) 1./myarea(x,y); % removes the infeasible region

plot(0,0,'k.','MarkerSize',25,'LineWidth',2);
hold on
grid on
plot(11/4,11/4,'k.','MarkerSize',25,'LineWidth',2);
fplot(mycurve,'k',[.9 3],'LineWidth',2)
fplot(myline,[-2 5],'k','LineWidth',2)
fsurf(marinv,[-2 5 -1,6],'EdgeColor','none','FaceAlpha',0.5)
colormap jet

コマンド ラインで「plottools」と入力し、矢の描画ツールを使用して矢を追加します。

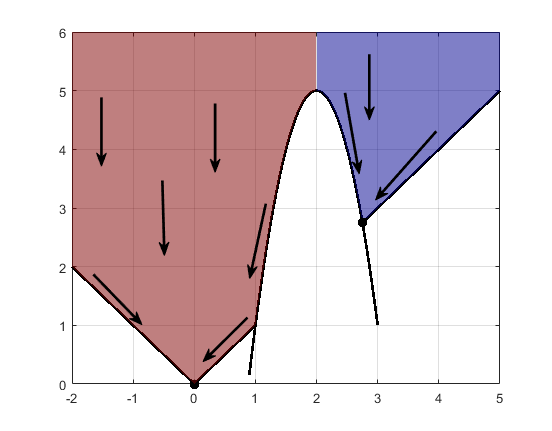
最急降下経路は制約境界までの直線です。制約境界から、最急降下経路は境界に沿って下に移動します。初期の x 値が 2 の上か下にあるかで異なりますが、最終点は (0,0) または (11/4,11/4) のどちらかです。

参考

トピック

• 引き込み領域を視覚化する
• 6 つのソルバーの比較