このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

`ga`を用いた制約付き最小化、問題ベース

この例では、問題ベースのアプローチで ga を使用して、非線形不等式制約と境界に従って目的関数を最小化する方法を示します。この問題のソルバーベースのバージョンについては、遺伝的アルゴリズムを用いた制約付き最小化を参照してください。

制約付き最小化問題

この問題では、最小化する適応度関数は、2 次元変数 X と Y の単純な関数です。

camxy = @(X,Y)(4 - 2.1.*X.^2 + X.^4./3).*X.^2 + X.*Y + (-4 + 4.*Y.^2).*Y.^2;

この関数についてはDixonとSzego [1]で説明されています。

さらに、この問題には非線形の制約と境界があります。

   x*y + x - y + 1.5 <= 0  (nonlinear constraint)
   10 - x*y <= 0           (nonlinear constraint)
   0 <= x <= 1             (bound)
   0 <= y <= 13            (bound)

非線形制約領域を適応度関数の表面プロット上にプロットします。制約により、解は両方の赤い曲線の上にある小さな領域に制限されます。

x1 = linspace(0,1);
y1 = (-x1 - 1.5)./(x1 - 1);
y2 = 10./x1;
[X,Y] = meshgrid(x1,linspace(0,13));
Z = camxy(X,Y);
surf(X,Y,Z,"LineStyle","none")
hold on
z1 = camxy(x1,y1);
z2 = camxy(x1,y2);
plot3(x1,y1,z1,'r-',x1,y2,z2,'r-')
xlim([0 1])
ylim([0 13])
zlim([0,max(Z,[],"all")])
hold off

Figure contains an axes object. The axes object contains 3 objects of type surface, line.

最適化変数、問題、制約を作成する

この問題を設定するには、最適化変数 x と y を作成します。変数を作成するときに境界を設定します。

x = optimvar("x","LowerBound",0,"UpperBound",1);
y = optimvar("y","LowerBound",0,"UpperBound",13);

最適化式として目標を作成します。

cam = camxy(x,y);

この目的関数を使用して最適化問題を作成します。

prob = optimproblem("Objective",cam);

2 つの非線形不等式制約を作成し、問題に含めます。

prob.Constraints.cons1 = x*y + x - y + 1.5 <= 0;
prob.Constraints.cons2 = 10 - x*y <= 0;

問題を確認します。

show(prob)

  OptimizationProblem : 

	Solve for:
       x, y

	minimize :
       (((((4 - (2.1 .* x.^2)) + (x.^4 ./ 3)) .* x.^2) + (x .* y)) + (((-4) + (4 .* y.^2)) .* y.^2))


	subject to cons1:
       ((((x .* y) + x) - y) + 1.5) <= 0

	subject to cons2:
       (10 - (x .* y)) <= 0

	variable bounds:
       0 <= x <= 1

       0 <= y <= 13

問題を解く

ga ソルバーを指定して問題を解きます。

[sol,fval] = solve(prob,"Solver","ga")

Solving problem using ga.
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

sol = struct with fields:
    x: 0.8122
    y: 12.3103

fval = 
9.1268e+04

視覚化を追加する

ソルバーの進行状況を観察するには、2 つのプロット関数を選択するオプションを指定します。プロット関数 gaplotbestf は、各反復における最適な目的関数の値をプロットし、プロット関数 gaplotmaxconstr は、各反復における最大制約違反をプロットします。これら 2 つのプロット関数をセル配列に設定します。また、Display オプションを 'iter' に設定して、コマンドウィンドウにソルバーの進行状況に関する情報を表示します。

options = optimoptions(@ga,...
    'PlotFcn',{@gaplotbestf,@gaplotmaxconstr},...
    'Display','iter');

options 引数を含めてソルバーを実行します。

[sol,fval] = solve(prob,"Solver","ga","Options",options)

Solving problem using ga.

Single objective optimization:
2 Variables
2 Nonlinear inequality constraints

Options:
CreationFcn:       @gacreationuniform
CrossoverFcn:      @crossoverscattered
SelectionFcn:      @selectionstochunif
MutationFcn:       @mutationadaptfeasible

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2520       91357.8            0      0
    2           4982       91324.1     4.55e-05      0
    3           7914       97166.6            0      0
    4          16145       91268.4    0.0009997      0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

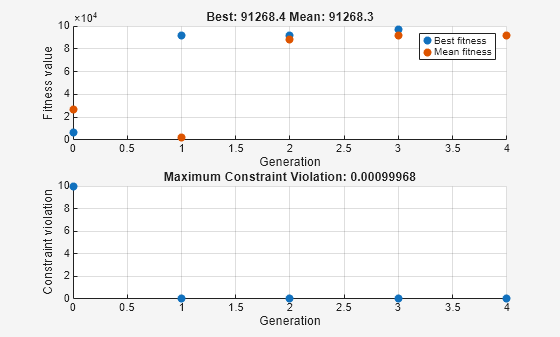
Figure Genetic Algorithm contains 2 axes objects. Axes object 1 with title Best: 91268.4 Mean: 91268.3, xlabel Generation, ylabel Fitness value contains 2 objects of type scatter. These objects represent Best fitness, Mean fitness. Axes object 2 with title Maximum Constraint Violation: 0.000999679, xlabel Generation, ylabel Constraint violation contains an object of type scatter.

sol = struct with fields:
    x: 0.8123
    y: 12.3103

fval = 
9.1268e+04

非線形制約により、ga は各反復で多くのサブ問題を解決します。プロットと反復表示の両方に示されているように、解決プロセスには反復がほとんどありません。ただし、反復表示の Func-count 列には、反復ごとに多数の関数評価が表示されます。

サポートされていない機能

目的関数または非線形制約関数がサポートされていない場合 (最適化変数および式でサポートされる演算を参照)、fcn2optimexpr を使用して、それらを問題ベースのアプローチに適した形式に変換します。たとえば、制約 $x y \geq 10$ の代わりに制約 $I_{1} (x) + I_{1} (y) \geq 10$ があり、 $I_{1} (x)$ が修正ベッセル関数 besseli(1,x) であるとします。(ベッセル関数はサポートされていない関数です。)この制約は fcn2optimexpr を使用して作成します。まず、 $I_{1} (x) + I_{1} (y)$ の最適化式を作成します。

bfun = fcn2optimexpr(@(t,u)besseli(1,t) + besseli(1,u),x,y);

次に、制約 cons2 を制約 bfun >= 10 に置き換えます。

prob.Constraints.cons2 = bfun >= 10;

問題を解きます。制約領域が異なるため、解も異なります。

[sol2,fval2] = solve(prob,"Solver","ga","Options",options)

Solving problem using ga.

Single objective optimization:
2 Variables
2 Nonlinear inequality constraints

Options:
CreationFcn:       @gacreationuniform
CrossoverFcn:      @crossoverscattered
SelectionFcn:      @selectionstochunif
MutationFcn:       @mutationadaptfeasible

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2512       974.044            0      0
    2           4974       960.998            0      0
    3           7436        963.12            0      0
    4          12001        960.83    0.0009335      0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

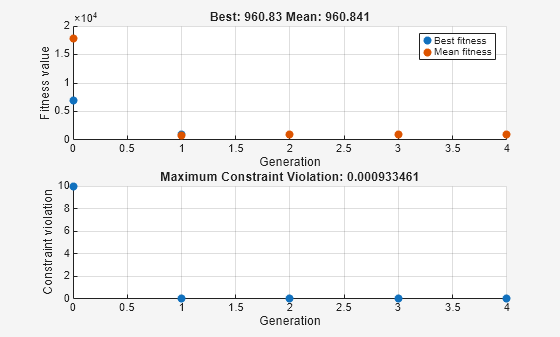
Figure Genetic Algorithm contains 2 axes objects. Axes object 1 with title Best: 960.83 Mean: 960.841, xlabel Generation, ylabel Fitness value contains 2 objects of type scatter. These objects represent Best fitness, Mean fitness. Axes object 2 with title Maximum Constraint Violation: 0.000933461, xlabel Generation, ylabel Constraint violation contains an object of type scatter.

sol2 = struct with fields:
    x: 0.4999
    y: 3.9979

fval2 = 
960.8300

参考文献

[1] Dixon, L. C. W., and G .P. Szego (eds.).Towards Global Optimisation 2.North-Holland:Elsevier Science Ltd., Amsterdam, 1978.

参考

ga | solve | fcn2optimexpr

gaを用いた制約付き最小化、問題ベース