Track Point Targets in Dense Clutter Using GM-PHD Tracker in Simulink
Radars generally receive echoes from all surfaces in the signal path. These unwanted back-scattered signals or echoes generated from physical objects are called clutter. In a densely cluttered environment, missed detections and false alarms make tracking objects a challenging task for conventional trackers such as Global Nearest-Neighbor (GNN) tracker. In such an environment a PHD tracker provides better estimation of objects as it can handle multiple detections per object per sensor without clustering them first. This example shows you how to track points targets in dense clutter using a Gaussian mixture probability hypothesis density (GM-PHD) tracker with a constant velocity model in Simulink. The example closely follows the Track Point Targets in Dense Clutter Using GM-PHD Tracker MATLAB® example.
Overview of the model
load_system('TrackPointTargetsInDenseClutterSimulinkExample'); set_param('TrackPointTargetsInDenseClutterSimulinkExample','SimulationCommand','update'); open_system('TrackPointTargetsInDenseClutterSimulinkExample');

The model consists of the four sections, each implementing a part of the workflow:
Scenario and Sensor Simulation
Tracking Algorithm
Performance Analysis
Visualization
Scenario and Sensor Simulation
In this example the scenario is created using trackingScenario. The scenario consists of five point targets moving at a constant velocity. You use the fusionRadarSensor to simulate radar detections in the scenario. The targets move within the field of view of the sensor. You use the FalseAlarmRate property of the sensor to control the density of the clutter. The value of the FalseAlarmRate property represents the probability of generating a false alarm in one resolution cell of the sensor. Based on a false alarm rate of 1e-3 and the resolution of the sensor defined in this example, there are approximately 53 false alarms generated per step. The scenario for this example is defined in helper file helperCreateClutterTrackingScenario. You use the Tracking Scenario Reader block to read the scenario object from the workspace. You configure the block to output detections along with platform poses and simulation time. The block output platform poses and detections as Simulink.Bus (Simulink) objects.
![]()
Tracking Algorithm
In this example you use the Probability Hypothesis Density (PHD) Tracker block with the gmphd filter to track targets. The first step towards configuring a PHD tracker is to define the configuration of the sensor. You define the sensor configuration as a structure with fields same as trackingSensorConfiguration. You set the SensorIndex of the configuration to 1 to match the index of the simulated sensor. As the sensor is a point object sensor that outputs at most one detection per object per scan, you set the MaxNumDetsPerObject field of the configuration as 1. You assume that all tracks are detectable, therefore, the SensorTransformFcn is defined as @(x,params)x and SensorLimits are defined as [-inf inf] for all states. You define the ClutterDensity field in the configuration, which refers to false alarm rate per-unit volume from the sensor. You set the FilterInitializationFcn to initcvgmphd, which creates a constant-velocity GM-PHD filter. You specify the birth rate of new targets from block mask to define the expected number of targets appearing in the field of view per unit time. Code for creating the sensor configuration is defined in the helper function helperCreateSensorConfig. You call this function in the PreLoadFcn callback. See Model Callbacks (Simulink) for more information about callback functions.
![]()
Performance Analysis

To evaluate the performance of the tracker, you use the Generalized Optimal Subpattern Assignment Metric block. The GOSPA metric aims to evaluate the performance of a tracker using a single combined score for errors in assignment and distance. The GOSPA metric can be calculated by the following equation:
![$GOSPA = [\sum_{i=0}^{m}(min(d_{b},c))^{p} + \frac{c^{p}}{\alpha} (n-m)]^{1/p}$](../../examples/fusion/win64/TrackPointTargetsInDenseClutterInSimulinkExample_eq08558369401179169166.png)
Where  is the number of ground truths and
is the number of ground truths and 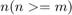 is the number of estimated tracks.
is the number of estimated tracks.  is the cutoff distance threshold, and
is the cutoff distance threshold, and 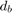 is the base distance between track and truth calculated by a distance function specified in the
is the base distance between track and truth calculated by a distance function specified in the Distance property. 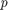 is order of the metric and
is order of the metric and  is the alpha parameter of the metric, defined from block mask.
is the alpha parameter of the metric, defined from block mask.
The lower GOSPA cost represents better tracking performance. A value of zero represents a perfect tracking. You enable Missed target error and False track error components of GOSPA metric as block outputs and visualize them. Before passing the truth information to the GOSPA metric block you remove the sensor platform from the truth information. To do this, you use the Helper Filter Sensor Platform helper block, implemented using MATLAB Function (Simulink) block.
Visualization
In this example the GOSPA metric is visualized using the scope block and the scenario is visualized using Scenario Visualization block. The Scenario Visualization block is implemented using MATLAB System (Simulink) block. Code for this block is defined in the helper class helperClutterTrackingDisplayBlock. The block uses RunTimeObject parameter of the blocks to display their outputs. See Access Block Data During Simulation (Simulink) for further information on how to access block outputs during simulation.
Notice that GOSPA metric decreases after a few steps. The initial value of GOSPA metric is higher due to the establishment delay for each track. The GOSPA metric results show that the GM-PHD tracker performed well in the densely cluttered scenario with zero false alarms and zero missed tracks.
close_system('TrackPointTargetsInDenseClutterSimulinkExample');
Summary
In this example you learned how to use a PHD tracker to track point objects in dense clutter in Simulink. You also learned how to evaluate performance of a tracking algorithm using GOSPA metric and its associated components. The simulation results show that the GM-PHD tracker does not miss targets or create false alarms. The lower overall GOSPA score also indicates desirable tracking performance.