このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

quaternion

quaternion 配列の作成

説明

四元数とは、3 次元の回転および方向に使用される、4 つの部分からなる多元数です。

四元数は、$$a+b\text{i}+c\text{j}+d\text{k}$$ の形式で表現されます。ここで、a、b、c、d の各部分は実数であり、i、j、k は等式 i² = j² = k² = ijk = −1 を満たす基底元です。

H で示される四元数の集合は、実数上の 4 次元ベクトル空間 R⁴ 内で定義されます。H の要素にはそれぞれ、基本要素 i、j、および k の線形結合に基づいた一意な表現があります。

3 次元での回転はすべて、回転の軸と、その軸を中心とした角度によって表現できます。四元数が回転行列より優れている点は、回転の軸と角度が解釈しやすいことです。たとえば、R³ 内の点について考えます。この点を回転するには、回転の軸と回転の角度を定義します。

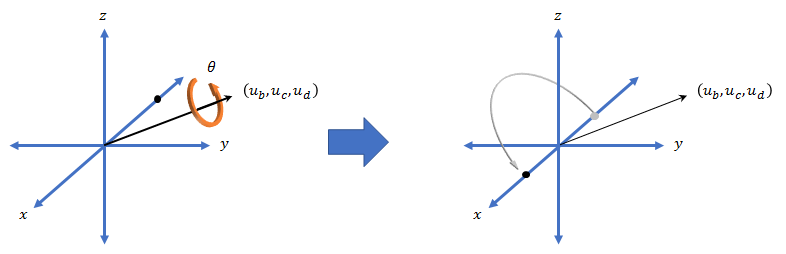
回転を四元数で表現すると、$$q=\cos \left(\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)+\sin \left(\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\left(u_b\text{i}+u_c\text{j}+u_d\text{k}\right)$$ として表すことができます。ここで θ は回転角度であり、[u_b、u_c、および u_d] は回転軸です。

作成

構文

quat = quaternion()

quat = quaternion(A,B,C,D)

quat = quaternion(matrix)

quat = quaternion(RV,"rotvec")

quat = quaternion(RV,"rotvecd")

quat = quaternion(RM,"rotmat",PF)

quat = quaternion(E,"euler",RS,PF)

quat = quaternion(E,"eulerd",RS,PF)

説明

quat = quaternion() は、空の四元数を作成します。

quat = quaternion(A,B,C,D) は quaternion 配列を作成し、四元数の 4 つの部分は配列 A、B、C、および D から取得されます。すべての入力が、同じサイズ、同じデータ型でなければなりません。

quat = quaternion(matrix) は、N 行 4 列の行列から N 行 1 列の quaternion 配列を作成し、各列が四元数の一部分となります。

quat = quaternion(RV,"rotvec") は、回転ベクトル RV の N 行 3 列の行列から N 行 1 列の quaternion 配列を作成します。RV の各行がそれぞれ 1 つの回転ベクトル (ラジアン単位) を表します。

quat = quaternion(RV,"rotvecd") は、回転ベクトル RV の N 行 3 列の行列から N 行 1 列の quaternion 配列を作成します。RV の各行がそれぞれ 1 つの回転ベクトル (度単位) を表します。

quat = quaternion(RM,"rotmat",PF) は、回転行列 RM の 3×3×N の配列から N 行 1 列の quaternion 配列を作成します。PF は、オイラー角が点の回転を表す場合は "point" となり、座標系の回転を表す場合は "frame" となります。

quat = quaternion(E,"euler",RS,PF) は、N 行 3 列の行列 E から N 行 1 列の quaternion 配列を作成します。E の各行は、それぞれ 1 セットのオイラー角 (ラジアン単位) を表します。E 内の角度は、シーケンス RS の座標軸を中心とした回転です。

quat = quaternion(E,"eulerd",RS,PF) は、N 行 3 列の行列 E から N 行 1 列の quaternion 配列を作成します。E の各行は、それぞれ 1 セットのオイラー角 (度単位) を表します。E 内の角度は、シーケンス RS の座標軸を中心とした回転です。

入力引数

A,B,C,D — 四元数の各部分

同じサイズのコンマ区切り配列

四元数の各部分。同じサイズの 4 つのコンマ区切りのスカラー、行列、または多次元配列として指定します。

例: quat = quaternion(1,2,3,4) は、1 + 2i + 3j + 4k の形式の四元数を作成します。

例: quat = quaternion([1,5],[2,6],[3,7],[4,8]) は、quat(1,1) = 1 + 2i + 3j + 4k および quat(1,2) = 5 + 6i + 7j + 8k である 1 行 2 列の quaternion 配列を作成します。

データ型: single | double

matrix — 四元数の各部分の行列

N 行 4 列の行列

四元数の各部分の行列。N 行 4 列の行列として指定します。行はそれぞれ別々の四元数を表します。列はそれぞれ別々の四元数の部分を表します。

例: quat = quaternion(rand(10,4)) は、10 行 1 列の quaternion 配列を作成します。

データ型: single | double

RV — 回転ベクトルの行列

N 行 3 列の行列

回転ベクトルの行列。N 行 3 列の行列として指定します。RV の各行は、回転ベクトルの [X Y Z] 要素を表します。回転ベクトルは、回転の角度 (ラジアン単位または度単位) でスケーリングされた回転の軸を表す単位ベクトルです。

この構文を使用するには、1 つ目の引数を回転ベクトルの行列として、2 つ目の引数を "rotvec" または "rotvecd" として指定します。

例: quat = quaternion(rand(10,3),"rotvec") は、10 行 1 列の quaternion 配列を作成します。

データ型: single | double

RM — 回転行列

3 行 3 列の行列 | 3×3×N の配列

回転行列の配列。3 行 3 列の行列または 3×3×N の配列として指定します。配列の各ページはそれぞれ別々の回転行列を表します。

例: quat = quaternion(rand(3),"rotmat","point")

例: quat = quaternion(rand(3),"rotmat","frame")

データ型: single | double

PF — 回転行列のタイプ

"point" | "frame"

回転行列のタイプ。"point" または "frame" によって指定します。

例: quat = quaternion(rand(3),"rotmat","point")

例: quat = quaternion(rand(3),"rotmat","frame")

データ型: char | string

E — オイラー角の行列

N 行 3 列の行列

オイラー角の行列。N 行 3 列の行列として指定します。"euler" 構文を使用する場合は、E をラジアン単位で指定します。"eulerd" 構文を使用する場合は、E を度単位で指定します。

例: quat = quaternion(E,"euler","YZY","point")

例: quat = quaternion(E,"euler","XYZ","frame")

データ型: single | double

RS — 回転シーケンス

文字ベクトル | スカラー string

回転シーケンス。3 要素の文字ベクトルとして指定します。

• "YZY"

• "YXY"

• "ZYZ"

• "ZXZ"

• "XYX"

• "XZX"

• "XYZ"

• "YZX"

• "ZXY"

• "XZY"

• "ZYX"

• "YXZ"

ある点の座標系が、座標系の回転を使用して回転されたときに、新しい座標を特定すると仮定します。この点は、元の座標系では以下のように定義されています。

point = [sqrt(2)/2,sqrt(2)/2,0];

この表現では、最初の列が x 軸を表し、2 番目の列が y 軸を表し、3 番目の列が z 軸を表しています。

オイラー角表現 [45,45,0] を使用して、点を回転します。点を回転するには、次の 2 つの異なる回転シーケンスを使用します。

• 四元数回転子を作成し、"ZYX" シーケンスを指定する場合、座標系はまず z 軸を中心に 45 度回転され、次に新しい y 軸を中心に 45 度回転されます。

  quatRotator = quaternion([45,45,0],"eulerd","ZYX","frame");
  newPointCoordinate = rotateframe(quatRotator,point)

  newPointCoordinate =
  
      0.7071   -0.0000    0.7071

  

• 四元数回転子を作成し、"YZX" シーケンスを指定する場合、座標系はまず y 軸を中心に 45 度回転され、次に新しい z 軸を中心に 45 度回転されます。

  quatRotator = quaternion([45,45,0],"eulerd","YZX","frame");
  newPointCoordinate = rotateframe(quatRotator,point)

  newPointCoordinate =
  
      0.8536    0.1464    0.5000

  

データ型: char | string

transformation — 同次変換

se3 オブジェクト | se3 オブジェクトの N 要素配列

変換。se3 オブジェクトとして、あるいは se3 オブジェクトの N 要素配列として指定します。N は変換の合計数です。

quaternion オブジェクトは変換の並進成分を無視し、変換のうち回転の 3 行 3 列の部分行列を quaternion に変換します。

rotation — 正規直交回転

so3 オブジェクト | so3 オブジェクトの N 要素配列

正規直交回転。so3 オブジェクトとして、あるいは so3 オブジェクトの N 要素配列として指定します。N は回転の合計数です。

オブジェクト関数

作成と変換

compact	quaternion 配列を N 行 4 列の行列に変換
eulerd	四元数をオイラー角 (度) に変換
euler	四元数をオイラー角 (ラジアン) に変換
rotmat	四元数の回転行列への変換
rotvec	四元数の回転ベクトルへの変換 (ラジアン単位)
rotvecd	四元数の回転ベクトルへの変換 (度単位)
ones	実数部が 1 に設定され、虚数部が 0 に設定された quaternion 配列を作成
parts	四元数の各部分の抽出
randrot	一様分布のランダムな回転
zeros	すべての部分が 0 に設定された quaternion 配列を作成

回転

rotateframe	四元数の座標系の回転
rotatepoint	四元数の点の回転

正規化

norm	四元数のノルム
normalize	四元数正規化

四元数の計算

angvel	quaternion 配列による角速度
dist	角距離 (ラジアン)
exp	quaternion 配列の指数
interp1	四元数の内挿 (テーブル ルックアップ)
log	quaternion 配列の自然対数
meanrot	四元数の平均回転
slerp	球面線形内挿

算術演算

conj	四元数の複素共役
ctranspose, '	quaternion 配列の複素共役転置
ldivide, .\	要素単位の四元数の左除算
minus, -	四元数の減算
mldivide, \	スカラーの四元数の左除算
mrdivide, /	スカラーの四元数の右除算
mtimes, *	四元数の乗算
power	要素単位の四元数のべき乗
prod	quaternion 配列の積
rdivide, ./	要素単位の四元数の右除算
times	要素単位の四元数の乗算
transpose, .'	quaternion 配列の転置
uminus, -	四元数の単項マイナス

例

空の四元数の作成

quat = quaternion()

quat = 

  0×0 empty quaternion array

既定では、四元数の基となるクラスは double です。

classUnderlying(quat)

ans = 
'double'

四元数の個々の部分を指定することによる四元数の作成

quaternion 配列を作成するには、4 つの部分を、同じサイズのコンマ区切りのスカラー、行列、または多次元配列として指定します。

四元数の各部分をスカラーとして定義します。

A = 1.1;
B = 2.1;
C = 3.1;
D = 4.1;
quatScalar = quaternion(A,B,C,D)

quatScalar = quaternion
     1.1 + 2.1i + 3.1j + 4.1k

四元数の各部分を列ベクトルとして定義します。

A = [1.1;1.2];
B = [2.1;2.2];
C = [3.1;3.2];
D = [4.1;4.2];
quatVector = quaternion(A,B,C,D)

quatVector = 2×1 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k
     1.2 + 2.2i + 3.2j + 4.2k

四元数の各部分を行列として定義します。

A = [1.1,1.3; ...
     1.2,1.4];
B = [2.1,2.3; ...
     2.2,2.4];
C = [3.1,3.3; ...
     3.2,3.4];
D = [4.1,4.3; ...
     4.2,4.4];
quatMatrix = quaternion(A,B,C,D)

quatMatrix = 2×2 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k     1.3 + 2.3i + 3.3j + 4.3k
     1.2 + 2.2i + 3.2j + 4.2k     1.4 + 2.4i + 3.4j + 4.4k

四元数の各部分を 3 次元配列として定義します。

A = randn(2,2,2);
B = zeros(2,2,2);
C = zeros(2,2,2);
D = zeros(2,2,2);
quatMultiDimArray = quaternion(A,B,C,D)

quatMultiDimArray = 2×2×2 quaternion array
quatMultiDimArray(:,:,1) = 

     0.53767 +       0i +       0j +       0k     -2.2588 +       0i +       0j +       0k
      1.8339 +       0i +       0j +       0k     0.86217 +       0i +       0j +       0k


quatMultiDimArray(:,:,2) = 

     0.31877 +       0i +       0j +       0k    -0.43359 +       0i +       0j +       0k
     -1.3077 +       0i +       0j +       0k     0.34262 +       0i +       0j +       0k

四元数の各部分の行列を指定することによる四元数の作成

四元数のスカラーまたは列ベクトルを作成するには、四元数の各部分の N 行 4 列の行列を指定します。列はそれぞれ、四元数の部分 A、B、C、D に対応します。

ランダムな四元数の列ベクトルを作成します。

quatParts = rand(3,4)

quatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

quat = quaternion(quatParts)

quat = 3×1 quaternion array
     0.81472 + 0.91338i +  0.2785j + 0.96489k
     0.90579 + 0.63236i + 0.54688j + 0.15761k
     0.12699 + 0.09754i + 0.95751j + 0.97059k

四元数表現から quatParts 行列を取得するには、compact を使用します。

retrievedquatParts = compact(quat)

retrievedquatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

回転ベクトルを指定することによる四元数の作成

N 行 1 列の quaternion 配列を作成するには、回転ベクトルの N 行 3 列の行列をラジアンまたは度単位で指定します。回転ベクトルは、正規化された四元数と 1 対 1 の関係をもつ、コンパクトな空間的表現です。

ラジアン単位の回転ベクトル

回転ベクトルを使用してスカラー quaternion を作成し、結果の四元数が正規化されていることを検証します。

rotationVector = [0.3491,0.6283,0.3491];
quat = quaternion(rotationVector,"rotvec")

quat = quaternion
     0.92124 + 0.16994i + 0.30586j + 0.16994k

norm(quat)

ans = 
1.0000

四元数からラジアン単位の回転ベクトルに変換するには、関数 rotvec を使用します。四元数 quat から rotationVector を復元します。

rotvec(quat)

ans = 1×3

    0.3491    0.6283    0.3491

度単位の回転ベクトル

回転ベクトルを使用してスカラー quaternion を作成し、結果の四元数が正規化されていることを検証します。

rotationVector = [20,36,20];
quat = quaternion(rotationVector,"rotvecd")

quat = quaternion
     0.92125 + 0.16993i + 0.30587j + 0.16993k

norm(quat)

ans = 
1

四元数から度単位の回転ベクトルに変換するには、関数 rotvecd を使用します。四元数 quat から rotationVector を復元します。

rotvecd(quat)

ans = 1×3

   20.0000   36.0000   20.0000

回転行列を指定することによる四元数の作成

回転行列の 3×3×N の配列を指定することによって、N 行 1 列の quaternion 配列を作成できます。回転行列配列の各ページは、quaternion 配列の 1 つの要素に対応します。

3 行 3 列の回転行列を使用して、スカラー quaternion を作成します。回転行列を、座標系か点のどちらの回転として解釈するかを指定します。

rotationMatrix = [1 0         0; ...
                  0 sqrt(3)/2 0.5; ...
                  0 -0.5      sqrt(3)/2];
quat = quaternion(rotationMatrix,"rotmat","frame")

quat = quaternion
     0.96593 + 0.25882i +       0j +       0k

四元数から回転行列に変換するには、関数 rotmat を使用します。四元数 quat から rotationMatrix を復元します。

rotmat(quat,"frame")

ans = 3×3

    1.0000         0         0
         0    0.8660    0.5000
         0   -0.5000    0.8660

オイラー角を指定することによる四元数の作成

N 行 3 列のオイラー角の配列をラジアンまたは度単位で指定することにより、N 行 1 列の quaternion 配列を作成できます。

ラジアン単位のオイラー角

euler 構文でラジアン単位のオイラー角の 1 行 3 列のベクトルを使用して、スカラー quaternion を作成します。オイラー角の回転シーケンスと、角度が座標系か点のどちらの回転を表すかを指定します。

E = [pi/2,0,pi/4];
quat = quaternion(E,"euler","ZYX","frame")

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

四元数からオイラー角に変換するには、関数 euler を使用します。四元数 quat からオイラー角 E を復元します。

euler(quat,"ZYX","frame")

ans = 1×3

    1.5708         0    0.7854

度単位のオイラー角

eulerd 構文で度単位のオイラー角の 1 行 3 列のベクトルを使用して、スカラー quaternion を作成します。オイラー角の回転シーケンスと、角度が座標系か点のどちらの回転を表すかを指定します。

E = [90,0,45];
quat = quaternion(E,"eulerd","ZYX","frame")

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

四元数から度単位のオイラー角に変換するには、関数 eulerd を使用します。四元数 quat からオイラー角 E を復元します。

eulerd(quat,"ZYX","frame")

ans = 1×3

   90.0000         0   45.0000

四元数代数

四元数は、実数上の非可換結合代数を形成します。この例は、四元数代数の規則を説明しています。

加算と減算

四元数の加算と減算は部分ごとに発生し、可換です。

Q1 = quaternion(1,2,3,4)

Q1 = quaternion
     1 + 2i + 3j + 4k

Q2 = quaternion(9,8,7,6)

Q2 = quaternion
     9 + 8i + 7j + 6k

Q1plusQ2 = Q1 + Q2

Q1plusQ2 = quaternion
     10 + 10i + 10j + 10k

Q2plusQ1 = Q2 + Q1

Q2plusQ1 = quaternion
     10 + 10i + 10j + 10k

Q1minusQ2 = Q1 - Q2

Q1minusQ2 = quaternion
    -8 - 6i - 4j - 2k

Q2minusQ1 = Q2 - Q1

Q2minusQ1 = quaternion
     8 + 6i + 4j + 2k

実数と四元数の加算や減算も実行できます。四元数の最初の部分は "実数" 部と呼ばれ、2 番目、3 番目、4 番目の部分は "ベクトル" と呼ばれます。実数を使用した加算および減算は、四元数の実数部のみに影響します。

Q1plusRealNumber = Q1 + 5

Q1plusRealNumber = quaternion
     6 + 2i + 3j + 4k

Q1minusRealNumber = Q1 - 5

Q1minusRealNumber = quaternion
    -4 + 2i + 3j + 4k

乗算

四元数の乗算は、基本要素の積と分配法則によって決まります。前述したように、基本要素 i、j、k の乗算は可換ではないため、四元数の乗算は可換ではありません。

Q1timesQ2 = Q1 * Q2

Q1timesQ2 = quaternion
    -52 + 16i + 54j + 32k

Q2timesQ1 = Q2 * Q1

Q2timesQ1 = quaternion
    -52 + 36i + 14j + 52k

isequal(Q1timesQ2,Q2timesQ1)

ans = logical
   0

四元数は実数で乗算することもできます。四元数を実数で乗算する場合、四元数の各部分が個別に実数で乗算されます。

Q1times5 = Q1*5

Q1times5 = quaternion
      5 + 10i + 15j + 20k

四元数の実数による乗算は可換です。

isequal(Q1*5,5*Q1)

ans = logical
   1

共役

四元数の複素共役は、quaternion のベクトル部分の各要素の符号を反転して定義されます。

Q1

Q1 = quaternion
     1 + 2i + 3j + 4k

conj(Q1)

ans = quaternion
     1 - 2i - 3j - 4k

四元数とその共役の間の乗算は可換です。

isequal(Q1*conj(Q1),conj(Q1)*Q1)

ans = logical
   1

quaternion 配列の操作

四元数を整理して、ベクトル、行列、多次元配列にまとめることができます。組み込みの MATLAB® 関数が、四元数に対応するように強化されています。

連結

四元数は、連結中は個々のオブジェクトとして処理され、配列の操作に関しては MATLAB の規則に従います。

Q1 = quaternion(1,2,3,4);
Q2 = quaternion(9,8,7,6);

qVector = [Q1,Q2]

qVector = 1×2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k

Q3 = quaternion(-1,-2,-3,-4);
Q4 = quaternion(-9,-8,-7,-6);

qMatrix = [qVector;Q3,Q4]

qMatrix = 2×2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMultiDimensionalArray(:,:,1) = qMatrix;
qMultiDimensionalArray(:,:,2) = qMatrix

qMultiDimensionalArray = 2×2×2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

インデックス

quaternion 配列で要素にアクセスしたり要素を割り当てたりするには、インデックスを使用します。

qLoc2 = qMultiDimensionalArray(2)

qLoc2 = quaternion
    -1 - 2i - 3j - 4k

インデックス 2 の quaternion を quaternion one に置き換えます。

qMultiDimensionalArray(2) = ones("quaternion")

qMultiDimensionalArray = 2×2×2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

形状変更

quaternion 配列の形状を変更するには、関数 reshape を使用します。

qMatReshaped = reshape(qMatrix,4,1)

qMatReshaped = 4×1 quaternion array
     1 + 2i + 3j + 4k
    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k
    -9 - 8i - 7j - 6k

転置

quaternion のベクトルおよび行列を転置するには、関数 transpose を使用します。

qMatTransposed = transpose(qMatrix)

qMatTransposed = 2×2 quaternion array
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

並べ替え

quaternion のベクトル、行列および多次元配列を並べ替えるには、関数 permute を使用します。

qMultiDimensionalArray

qMultiDimensionalArray = 2×2×2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMatPermute = permute(qMultiDimensionalArray,[3,1,2])

qMatPermute = 2×2×2 quaternion array
qMatPermute(:,:,1) = 

     1 + 2i + 3j + 4k     1 + 0i + 0j + 0k
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k


qMatPermute(:,:,2) = 

     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2018b で導入

R2025a: interp1 オブジェクト関数による四元数の内挿

SQUAD や SLERP などの内挿法を使用して四元数を内挿するには、interp1 オブジェクト関数を使用します。

R2025a: slerp オブジェクト関数による自然な内挿のサポート

slerp 関数で "natural" パス オプションを使用した球面に沿った内挿がサポートされるようになり、始点と終点の四元数の向きに沿った、より滑らかな遷移が可能になりました。

参考

se3 | so3 | randrot

トピック

• Rotations, Orientation, and Quaternions
• Lowpass Filter Orientation Using Quaternion SLERP