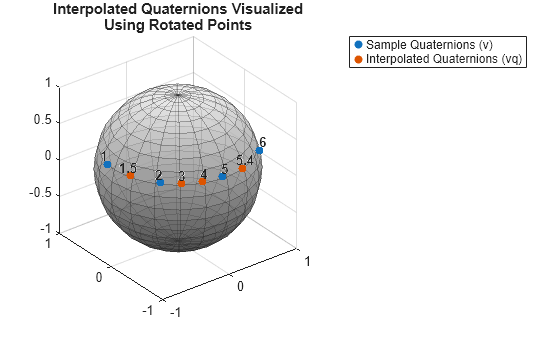
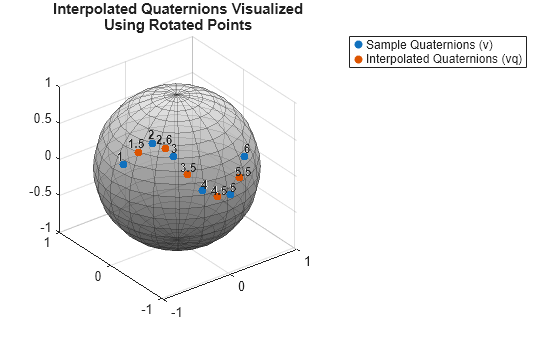
interp1
構文
説明
例
入力引数
出力引数
アルゴリズム
参照
[1] Shoemake, Ken. "Animating Rotation with Quaternion Curves." ACM SIGGRAPH Computer Graphics 19, no. 3 (July 1985): 245–54. https://doi.org/10.1145/325165.325242.
[2] Dam, Erik B., Martin Koch, and Martin Lillholm. Quaternions, Interpolation and Animation. Technical Report DIKU-TR-98/5. Department of Computer Science, University of Copenhagen, July 17, 1998. https://web.mit.edu/2.998/www/QuaternionReport1.pdf.
拡張機能
バージョン履歴
R2025a で導入