精度の最大化

精度は勾配により制限されます。精度を最大化するには、勾配をできるだけ小さくする一方で、妥当な大きさの範囲を確保しなければなりません。バイアスは、勾配に伴って調整されます。

最大と最小の実際値が max(V) と min(V) でそれぞれ与えられるとします。これらの制限は、物理的原理またはエンジニアリングの考慮事項に基づいて既知となる場合があります。精度を最大化するには、丸めスキームと、オーバーフローを飽和させるかラップさせるかを決定しなければなりません。この例では簡潔化を図るために、最小実際値が最小エンコード値に対応しており、最大実際値が最大エンコード値に対応していることを前提としています。スケーリングで説明しているエンコードスキームを使用すると、これらの値は次のように与えられます。

$\begin{matrix} \max (V) = F 2^{E} (\max (Q)) + B \\ \min (V) = F 2^{E} (\min (Q)) + B . \end{matrix}$

勾配を求める式は次のとおりです。

$F 2^{E} = \frac{\max (V) - \min (V)}{\max (Q) - \min (Q)} = \frac{\max (V) - \min (V)}{2^{w s} - 1} .$

この式は、丸めやオーバーフローの問題には影響を受けず、ワードサイズ ws のみに依存します。

後続のゼロを使用したパディング

後続のゼロを使用したパディングでは、余分なビットを含む数の最下位ビット (LSB) が拡張されます。この方法では、精度が向上します。

たとえば、2 つの数値を互いに差し引くとします。まず、指数を整列しなければなりません。通常は、小さい方の数を右にシフトします。このシフトによって、有効桁数が右に "はみ出る" 場合があります。ただし、適切な数のビットを付加すると、結果の精度が最大化されます。値が近い 2 つの 8 ビットの固定小数点数を互いに差し引く場合を考えてみましょう。

$1.0000000 \times 2^{q} - 1.1111111 \times 2^{q - 1},$

ここで、q は整数です。この演算を実行するには、指数が等しくなければなりません。

$\begin{matrix} 1.0000000 \times 2^{q} \\ \frac{- 0.1111111 \times 2^{q}}{0.0000001 \times 2^{q}} . \end{matrix}$

上の数に 2 つのゼロを付加し、下の数に 1 つのゼロを付加すると、上の式は次のようになります。

$\begin{matrix} 1.000000000 \times 2^{q} \\ \frac{- 0.111111110 \times 2^{q}}{0.000000010 \times 2^{q}}, \end{matrix}$

これによってさらに正確な結果が生み出されます。

最高精度のための定数のスケーリング

次の固定小数点 Simulink^® ブロックは、値が定数ベクトルまたは定数行列であるパラメーターをスケーリングするためのモードを提供します。

このスケーリングモードは、2 進小数点のみのスケーリングに基づいています。このモードを使用すると、共通の 2 進小数点がベクトルまたは行列内の最大値に対する最高精度に基づいて求められるように、定数ベクトルまたは定数行列をスケーリングできます。

最高精度の定数スケーリングは、スケーリングが指定されていない固定小数点データ型に対してのみ使用できます。その他すべての固定小数点データ型は、指定されたスケーリングを使用します。ブロックのダイアログボックスで [データ型アシスタント] (データ型アシスタントを利用したデータ型の指定を参照) を使用すると、最高精度のスケーリングモードを有効にできます。

ブロックのダイアログボックスで、[データ型アシスタントを表示] ボタンをクリックします。
[データ型アシスタント] が表示されます。
[データ型アシスタント] の [モード] リストで、[固定小数点] を選択します。
[データ型アシスタント] に、固定小数点データ型に関連付けられている追加のオプションが表示されます。
[スケーリング] リストで、[最高精度] を選択します。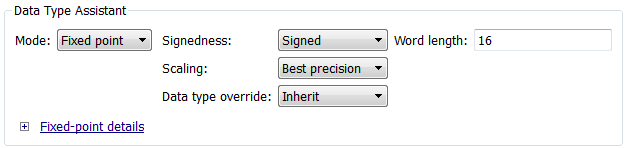

このスケーリングモードをどのように使用するかについて理解するために、次のように定義された double の 3 行 3 列の行列 M を考えてみましょう。

  3.3333e-003  3.3333e-004  3.3333e-005
  3.3333e-002  3.3333e-003  3.3333e-004
  3.3333e-001  3.3333e-002  3.3333e-003

ここで、M を Gain ブロックの [ゲイン] パラメーターの値として指定するとします。独自のスケーリングを指定した結果と定数スケーリングモードを使用した結果についてここで説明します。

指定したスケーリング
行列要素が 2^-7 の 2 進数小数点のみのスケーリングを使用して、10 ビット符号付きの汎用固定小数点データ型に変換されるとします (つまり、2 進小数点は右端のビットの 7 桁左に位置します)。このデータ形式では、M は次のようになります。
```
0            0            0
3.1250e-002  0            0
3.3594e-001  3.1250e-002  0
```
行列要素の多くはゼロであり、ゼロ以外のエントリに対しては、スケーリングされた値が元の値と異なることに注意してください。これは、各要素に対して固定サイズで制限された精度をもつバイナリワードに double が変換されるためです。変換データ型が大きく、正確なほど、スケーリングされた値は元の値に近くなります。
最高精度のための定数のスケーリング
M がその最大行列値に基づいてスケーリングされる場合は、次の結果が得られます。
```
2.9297e-003  0            0
3.3203e-002  2.9297e-003  0
3.3301e-001  3.3203e-002  2.9297e-003
```
最高精度によって、量子化誤差を最小にする小数部の長さが自動的に選択されます。精度が所定の語長に対して最大化されていても、量子化誤差が発生する場合があります。この例では、一部の要素がゼロに量子化されます。