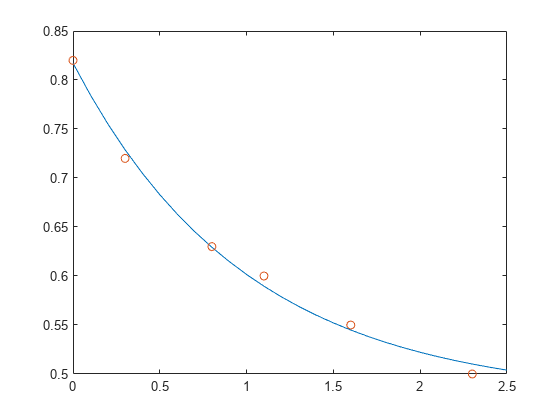
fixed.qrMatrixSolve

QR 分解を使用した x に対する連立線形方程式 Ax = B の求解

構文

x = fixed.qrMatrixSolve(A,B)

x = fixed.qrMatrixSolve(A,B, outputType)

x = fixed.qrMatrixSolve(A,B,outputType,regularizationParameter)

説明

x = fixed.qrMatrixSolve(A,B) は QR 分解を使用して連立線形方程式 Ax = B を解きます。

x = fixed.qrMatrixSolve(A,B, outputType) は、連立線形方程式 Ax = B の解を、outputType で指定された出力型をもつ変数として返します。

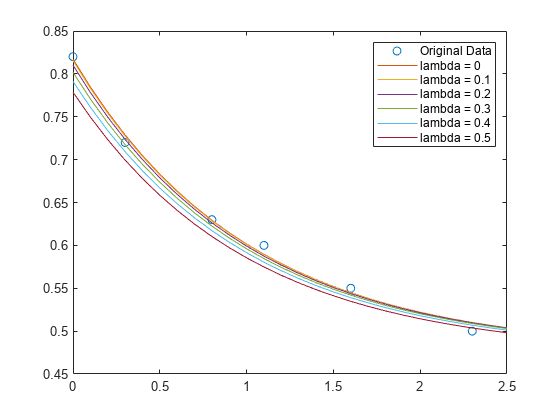
x = fixed.qrMatrixSolve(A,B,outputType,regularizationParameter) は、次の連立線形方程式の解を返します。

$$\left[\begin{array}{l}\lambda I_n\\ A\end{array}\right]x=\left[\begin{array}{l}{0}_{n,p}\\ B\end{array}\right]$$

ここで、A は m 行 n 列の行列、B は m 行 p 列の行列、λ は正則化パラメーターです。

例

QR 分解を使用した連立方程式の求解

この例では、QR 分解を使用して単純な連立線形方程式 $\mathit{Ax}=\mathit{b}$ を解く方法を示します。

この例では、A を、大きな条件数をもつ 5 行 3 列の行列として定義します。悪条件 (大きな条件数) の非正方行列を含む連立線形方程式を解くには、QR 分解を使用しなければなりません。

rng default;
A = gallery('randsvd', [5,3], 1000000);
b = [1; 1; 1; 1; 1];
x = fixed.qrMatrixSolve(A,b)

x = 3×1
104 ×

   -2.3777
    7.0686
   -2.2703

関数 fixed.qrMatrixSolve の結果を、関数 mldivide または \ の結果と比較します。

x = A\b

x = 3×1
104 ×

   -2.3777
    7.0686
   -2.2703

過決定システムでの正則化パラメーターの指定

この例では、過決定システムを解く際の正則化パラメーターの影響を示します。この例の量 y は、時間 t のいくつかの異なる値で測定され、次の観測値を生成します。

t = [0 .3 .8 1.1 1.6 2.3]';
y = [.82 .72 .63 .60 .55 .50]';

減衰指数関数を使用してデータをモデル化します。

$y(t)=c_1+c_2{e}^{-t}$.

上記の式は、ベクトル y が他の 2 つのベクトルの線形結合で近似されることを示しています。一方はすべて 1 の定数ベクトルであり、もう一方は成分 exp(-t) を含むベクトルです。未知の係数 $$c_1$$ および $$c_2$$ は、モデルのデータの偏差の二乗和を最小化する最小二乗近似を実行することで計算可能です。6 つの方程式と 2 つの未知数があり、6 行 2 列の行列で表されます。

E = [ones(size(t)) exp(-t)]

E = 6×2

    1.0000    1.0000
    1.0000    0.7408
    1.0000    0.4493
    1.0000    0.3329
    1.0000    0.2019
    1.0000    0.1003

関数 fixed.qrMatrixSolve を使用して最小二乗解を求めます。

c = fixed.qrMatrixSolve(E, y)

c = 2×1

    0.4760
    0.3413

つまり、データの最小二乗近似は次のようになります。

$$y(t)=0.4760+0.3413e^{-t}.$$

次のステートメントでは、t を等間隔にインクリメントしてモデルを評価し、結果を元のデータとともにプロットします。

T = (0:0.1:2.5)';
Y = [ones(size(T)) exp(-T)]*c;
plot(T,Y,'-',t,y,'o')

入力行列が悪条件である場合、正則化パラメーターを小さい正の値にすると、最小二乗問題の調整を向上させ、推定値の分散を小さくすることができます。このデータの最小二乗解に対する正則化パラメーターの影響を確認します。

figure;
lambda = [0:0.1:0.5];
plot(t,y,'o', 'DisplayName', 'Original Data');
for i = 1:length(lambda)
 c = fixed.qrMatrixSolve(E, y, numerictype('double'), lambda(i));
 Y = [ones(size(T)) exp(-T)]*c;
 hold on
 plot(T,Y,'-', 'DisplayName', ['lambda =', num2str(lambda(i))])
end
legend('Original Data', 'lambda = 0', 'lambda = 0.1', 'lambda = 0.2', 'lambda = 0.3', 'lambda = 0.4', 'lambda = 0.5')

入力引数

A — 係数行列

行列

連立線形方程式 Ax = B の係数行列。

データ型: single | double | fi
複素数のサポート: あり

B — 入力配列

ベクトル | 行列

連立線形方程式 Ax = B の B を表す入力ベクトルまたは行列。

データ型: single | double | fi
複素数のサポート: あり

outputType — 出力データ型

numerictype オブジェクト | 数値変数

出力データ型。numerictype オブジェクトまたは数値変数として指定します。outputType が numerictype オブジェクトとして指定されている場合、出力 x は指定されたデータ型をもちます。outputType が数値変数として指定されている場合、x はその数値変数と同じデータ型をもちます。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | fi | numerictype

regularizationParameter — 正則化パラメーター

0 (既定値) | 非負のスカラー

正則化パラメーター。非負のスカラーとして指定します。正則化パラメーターを小さい正の値にすると、問題の調整を向上させ、推定値の分散を小さくすることができます。バイアスがありますが、推定値の分散が小さいと、多くの場合、最小二乗推定値と比べて平均二乗誤差が小さくなります。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi

出力引数

x — 解決法

ベクトル | 行列

解。ベクトルまたは行列として返されます。A が m 行 n 列の行列で B が m 行 p 列の行列の場合、x は n 行 p 列の行列です。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

倍精度、単精度および固定小数点データ型のコードを生成します。

固定小数点の変換

Fixed-Point Designer™ を使用して固定小数点システムの設計とシミュレーションを行います。

A と B は符号付きで、2 進小数点スケーリングを使用しなければなりません。傾きとバイアス表現は固定小数点データ型ではサポートされていません。

バージョン履歴

R2020b で導入

参考

fixed.backwardSubstitute | fixed.forwardSubstitute | fixed.qlessQR | fixed.qlessQRUpdate | fixed.qrAB | fixed.qlessQRMatrixSolve

トピック

• Algorithms to Determine Fixed-Point Types for Complex Least-Squares Matrix Solve AX=B
• Determine Fixed-Point Types for Complex Least-Squares Matrix Solve AX=B
• Algorithms to Determine Fixed-Point Types for Real Least-Squares Matrix Solve AX=B
• Determine Fixed-Point Types for Real Least-Squares Matrix Solve AX=B