浅層ニューラルネットワークの汎化の改善と過適合の回避

ヒント

深層学習ネットワークのパラメーターを設定する方法については、パラメーターの設定と畳み込みニューラルネットワークの学習を参照してください。

ニューラルネットワークの学習中に起こる問題の 1 つは、過適合と呼ばれるものです。学習セットにおける誤差は非常に小さい値になりますが、新しいデータがネットワークに与えられると誤差は大きくなります。ネットワークは学習例を記憶しますが、新しい状況に対して汎化するようには学習は行われません。

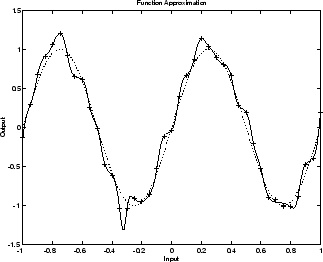
次の図は、ノイズを含む正弦関数を近似するように学習を行った 1-20-1 のニューラルネットワークの応答を示したものです。基となる正弦関数を点線で、ノイズを含む測定値を + 記号で表し、ニューラルネットワークの応答を実線で示しています。明らかに、このネットワークはデータに過適合していて、適切に汎化されていません。

Output versus input for a neural network trained to approximate a noisy sine function. The solid line goes through nearly all of the plus symbols representing the noisy data.

ネットワークの汎化を改善する手法の 1 つは、適当な近似を実現できるちょうど良い大きさのネットワークを使用することです。使用するネットワークが大きくなればなるほど、ネットワークが作成できる関数はより複雑になります。十分に小さいネットワークを使用する場合、データに過適合するだけの能力がありません。ネットワークのサイズを削減することによってどのように過適合を防ぐことができるかを調べるには、"Neural Network Design" の例 nnd11gn [HDB96] を実行してください。

残念ながら、特定のアプリケーションに対して適切なネットワークの大きさを前もって知ることは困難です。Deep Learning Toolbox™ ソフトウェアに実装されている汎化の改善方法として他に、正則化と早期停止の 2 つがあります。この後の各節では、これら 2 つの方法と、これらを実装するためのルーチンを説明します。

ネットワーク内のパラメーターの数が、学習セット内の点の総数よりはるかに少ない場合には、過適合の可能性はほとんどあるいはまったくありません。データの収集が容易で、学習データセットのサイズを増やすことができるのであれば、これから説明する過適合を防止する手法について考慮する必要はありません。この節の残りの部分が適用されるのは、入手できる限られたデータを最大限に活用する必要がある場合のみです。

ニューラルネットワークの再学習

一般的に、それぞれの逆伝播学習セッションは、初期の重みとバイアスのほか、データの学習セット、検証セット、テストセットへの分割は異なるものを使用して開始されます。このように条件が変わることにより、同じ問題に対しても得られる解が大きく異なる可能性があります。

適切に汎化されたネットワークを確実に求めるには、複数のネットワークに学習させることをお勧めします。

ここではデータセットを読み込んで 2 つの部分に分割します。90% はネットワークの設計用、10% はすべてのネットワークのテスト用です。

[x, t] = bodyfat_dataset;
Q = size(x, 2);
Q1 = floor(Q * 0.90);
Q2 = Q - Q1;
ind = randperm(Q);
ind1 = ind(1:Q1);
ind2 = ind(Q1 + (1:Q2));
x1 = x(:, ind1);
t1 = t(:, ind1);
x2 = x(:, ind2);
t2 = t(:, ind2);

次に、ネットワークアーキテクチャを選択し、データセットの最初の部分について学習を 10 回行います。その際に、データセットの 2 番目の部分について各ネットワークの平均二乗誤差も求めます。

net = feedforwardnet(10);
numNN = 10;
NN = cell(1, numNN);
perfs = zeros(1, numNN);
for i = 1:numNN
  fprintf('Training %d/%d\n', i, numNN);
  NN{i} = train(net, x1, t1);
  y2 = NN{i}(x2);
  perfs(i) = mse(net, t2, y2);
end

ネットワークごとに、初期の重みとバイアスのほか、最初のデータセットの学習セット、検証セット、テストセットへの分割は異なるものを使用して学習を開始します。テストセットはそれぞれのネットワークの汎化の程度を測る良い尺度ですが、すべてのネットワークに対するものではないことに注意してください。あるネットワーク用のテストセットのデータは、他のニューラルネットワークの学習または検証に使用される可能性が高いためです。そのため、元のデータセットを 2 つの部分に分割し、完全に独立したテストセットを確保しています。

性能が最も低いニューラルネットワークが、データセットの 2 番目の部分に対して最もよく汎化されたネットワークです。

複数のニューラルネットワーク

汎化を改善するためのもう 1 つの簡単な方法は、複数のニューラルネットワークの学習を行い、その出力を平均することです。特にノイズを含むデータまたは小規模なデータセットを使用する場合に簡単に利用できます。

例として、ここでは小さな問題に対して 10 個のニューラルネットワークの学習を行い、各ネットワークの平均二乗誤差を、全体平均の平均二乗誤差と比較します。

最初に、データセットを読み込み、設計セットとテストセットに分割します。

[x, t] = bodyfat_dataset;
Q = size(x, 2);
Q1 = floor(Q * 0.90);
Q2 = Q - Q1;
ind = randperm(Q);
ind1 = ind(1:Q1);
ind2 = ind(Q1 + (1:Q2));
x1 = x(:, ind1);
t1 = t(:, ind1);
x2 = x(:, ind2);
t2 = t(:, ind2);

それから、10 個のニューラルネットワークの学習を行います。

net = feedforwardnet(10);
numNN = 10;
nets = cell(1, numNN);
for i = 1:numNN
  fprintf('Training %d/%d\n', i, numNN)
  nets{i} = train(net, x1, t1);
end

次に、各ネットワークを 2 番目のデータセットについてテストし、個々の性能と、平均出力の性能を計算します。

perfs = zeros(1, numNN);
y2Total = 0;
for i = 1:numNN
  neti = nets{i};
  y2 = neti(x2);
  perfs(i) = mse(neti, t2, y2);
  y2Total = y2Total + y2;
end
perfs
y2AverageOutput = y2Total / numNN;
perfAveragedOutputs = mse(nets{1}, t2, y2AverageOutput)

平均出力の平均二乗誤差は、個々の性能の大半よりも通常は低くなりますが、すべてについて低くなるとは限りません。追加される新しいデータに対して良好に汎化される可能性が高くなります。

一部の非常に難しい問題に対しては、100 個のネットワークの学習を行い、任意の入力に対してその出力の平均を取ることができます。これは、ノイズを含む小規模なデータセットと以下で説明するベイズ正則化学習関数 trainbr を組み合わせて使用する場合に特に便利です。

早期停止

汎化の改善のための既定の方法は、"早期停止" と呼ばれます。この手法は、feedforwardnet などの逆伝播ネットワーク作成関数をはじめとする教師ありネットワーク作成関数のすべてで自動的に行われます。

この手法では、使用可能なデータを 3 つのサブセットに分割します。1 つ目のサブセットは学習セットです。これは勾配の計算と、ネットワークの重みとバイアスの更新に使用されます。2 つ目のサブセットは検証セットです。検証セットの誤差は学習プロセスの間、監視されます。検証誤差は通常、学習セットの誤差と同様に、学習の初期段階に減少します。ただし、ネットワークがデータに過適合し始めると、検証セットの誤差は一般に増加し始めます。検証誤差が、指定した反復回数 (net.trainParam.max_fail) にわたって増加すると、学習は停止し、検証誤差の最小値での重みとバイアスが返されます。

テストセットの誤差は学習中は使用されませんが、さまざまなモデルの比較に使用されます。学習プロセス中にテストセットの誤差をプロットするのも有益です。テストセットの誤差が検証セットの誤差と比べて有意に異なる反復回数で最小値に到達する場合、データセットの分割が不適切である可能性を示しています。

データを学習セット、検証セット、およびテストセットに分割するために 4 つの関数が用意されています。dividerand (既定)、divideblock、divideint、および divideind です。ネットワークの分割関数は、次のプロパティを使用してアクセスまたは変更できます。

net.divideFcn

これらの各関数には、動作をカスタマイズするパラメーターがあります。これらの値は、次のネットワークプロパティに保存され、変更できます。

net.divideParam

インデックスデータ分割 (divideind)

シンプルなテスト問題を作成します。データセット全体として、−1 から 1 までの範囲で 0.01 ステップの 201 個の入力点を持つ、ノイズを含む正弦波を生成します。

p = [-1:0.01:1];
t = sin(2*pi*p)+0.1*randn(size(p));

連続した標本が学習セット、検証セット、テストセットに連続的に割り当てられるように、インデックスでデータを分割します。

trainInd = 1:3:201
valInd = 2:3:201;
testInd = 3:3:201;
[trainP,valP,testP] = divideind(p,trainInd,valInd,testInd);
[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

ランダムデータ分割 (dividerand)

次のように、標本のうち 60% が学習セットに、20% が検証セットに、20% がテストセットに割り当てられるように、入力データをランダムに分割できます。

[trainP,valP,testP,trainInd,valInd,testInd] = dividerand(p);

この関数は入力データを分割するだけでなく、インデックスも返します。そのため、divideind を使用してターゲットデータを適宜分割できます。

[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

ブロックデータ分割 (divideblock)

次のように、標本のうち最初の 60% が学習セットに、次の 20% が検証セットに、最後の 20% がテストセットに割り当てられるように、入力データをランダムに分割することもできます。

[trainP,valP,testP,trainInd,valInd,testInd] = divideblock(p);

divideind を使用してターゲットデータを適宜分割します。

[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

インターリーブデータ分割 (divideint)

入力データを分割するもう 1 つの方法は、割合に従って標本を学習セット、検証セット、テストセット間で循環するように割り当てることです。標本のうち 60% が学習セットに、20% が検証セットに、20% がテストセットに割り当てられるように、インターリーブすることができます。

[trainP,valP,testP,trainInd,valInd,testInd] = divideint(p);

divideind を使用してターゲットデータを適宜分割します。

[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

正則化

汎化の改善のためのもう 1 つの方法は、正則化と呼ばれます。この際、性能関数が修正されます。性能関数は通常、学習セットに対するネットワーク誤差の平方和が選択されます。次の節では性能関数の修正方法を説明し、その次の節では、最も良い汎化が行われるように最適な性能関数を自動的に設定するルーチンを説明します。

修正された性能関数

フィードフォワードニューラルネットワークの学習に使用される典型的な性能関数は、ネットワーク誤差の平均平方和です。

$F = m s e = \frac{1}{N} \sum_{i = 1}^{N} {(e_{i})}^{2} = \frac{1}{N} \sum_{i = 1}^{N} {(t_{i} - α_{i})}^{2}$

ネットワークの重みとバイアスの平均平方和で構成される項 $m s e r e g = γ * m s w + (1 - γ) * m s e$ を追加して性能関数を修正すると、汎化を改善できます。ここで、 $γ$ は性能比です。

$m s w = \frac{1}{n} \sum_{j = 1}^{n} w_{j}^{2}$

この性能関数を使うと、ネットワークの重みとバイアスは小さくなり、ネットワークの応答は強制的に滑らかになるため過適合しにくくなります。

次のコードは、前述のネットワークを再初期化して、正則化された性能関数で BFGS アルゴリズムを使用して再学習を行います。ここで、性能比を 0.5 に設定します。これにより、重みは平均二乗誤差と平均二乗重みに等しくなります

[x,t] = simplefit_dataset;
net = feedforwardnet(10,'trainbfg');
net.divideFcn = '';
net.trainParam.epochs = 300;
net.trainParam.goal = 1e-5;
net.performParam.regularization = 0.5;
net = train(net,x,t);

正則化の問題は、性能比パラメーターの最適な値を決定することが困難であることです。このパラメーターを大きくしすぎると、過適合になる可能性があります。比が小さすぎると、ネットワークは学習データにうまく当てはまらなくなります。次の節では、正則化パラメーターを自動的に設定するルーチンについて説明します。

自動正則化 (trainbr)

最適な正則化パラメーターは、自動的に決定することをお勧めします。このプロセスへのアプローチの 1 つは、David MacKay [MacK92] のベイズフレームワークです。このフレームワークでは、ネットワークの重みとバイアスが、指定の分布を持つ確率変数であると仮定されます。正則化パラメーターは、これらの分布に関連付けられた未知の分散に関連しています。これらのパラメーターは、統計的手法を使用して推定できます。

ベイズ正則化の詳細は、このユーザーガイドで扱う範囲を超えています。レーベンバーグ・マルカート法学習と組み合わせたベイズ正則化の使用方法の詳細な説明は、[FoHa97] を参照してください。

ベイズ正則化は関数 trainbr に実装されています。次のコードは、浅層ニューラルネットワークの汎化の改善と過適合の回避の図に示したノイズを含む正弦波を近似するための関数を使用して、1-20-1 のネットワークに学習させる方法を示したものです (データ分割は net.divideFcn を設定することでキャンセルされ、trainbr の効果は早期停止から分離されます)。

x = -1:0.05:1;
t = sin(2*pi*x) + 0.1*randn(size(x));
net = feedforwardnet(20,'trainbr');
net = train(net,x,t);

このアルゴリズムの特徴の 1 つは、何個のネットワークパラメーター (重みとバイアス) がネットワークで実質的に使用されているかを示す尺度を提供することです。この場合、最終的な学習済みネットワークは、1-20-1 のネットワークの合計 61 個の重みとバイアスのうち、約 12 個のパラメーター (出力では #Par で表示) を使用しています。この有効なパラメーターの数は、ネットワークのパラメーターの数が多くてもほぼ同じのままになります (確実に収束するように十分な反復回数にわたってネットワークの学習が行われたと仮定しています)。

trainbr アルゴリズムは、一般的にネットワーク入力とターゲットがほぼ [−1,1] の範囲に含まれるようスケーリングされている場合に、最も効果的です。ここでのテスト問題はこれに該当します。入力とターゲットがこの範囲に収まらない場合は、ニューラルネットワーク入出力処理関数の選択で説明している関数 mapminmax または mapstd を使用してスケーリングできます。feedforwardnet で作成したネットワークには、既定で入出力処理関数として mapminmax が含まれます。

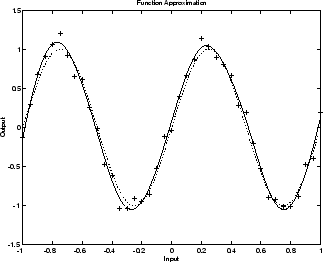
次の図は、学習済みネットワークの応答を示しています。1-20-1 のネットワークがデータに過適合している前述の図とは対照的に、ここでは、ネットワークの応答が基となる正弦関数 (点線) と非常に近く、そのためネットワークは新たな入力に対して適切に汎化されます。これよりも大きいネットワークを試しても、ネットワークの応答がデータに過適合することはありません。これにより、最適なネットワークのサイズを決定するために必要な推測を避けることができます。

trainbr を使用する場合、有効なパラメーターの数が収束するまでアルゴリズムを実行させることが重要になります。学習は、"Maximum MU reached" というメッセージを出力して停止する場合があります。これは一般的なもので、アルゴリズムが実際に収束したことを適切に示します。また、複数回反復しても残差平方和 (SSE) や重み平方和 (SSW) が相対的に一定の値になる場合は、アルゴリズムが収束したと言えます。この状態になれば、学習ウィンドウの停止ボタンをクリックしてもかまいません。

Output versus input for a neural network trained to approximate a noisy sine function. The solid line closely matches the dotted line representing the underlying sine function.

早期停止と正則化のまとめと考察

早期停止と正則化は、適切に適用すると、ネットワークの汎化を確保できます。

早期停止では、収束が速すぎるアルゴリズムを使用しないよう注意しなければなりません。高速なアルゴリズム (trainlm など) を使用している場合は、収束が比較的遅くなるように学習パラメーターを設定してください。たとえば mu を 1 などの比較的大きな値に設定したり、mu_dec と mu_inc をそれぞれ 0.8 と 1.5 などの 1 に近い値に設定したりします。学習関数 trainscg と trainbr は、通常は早期停止で良好に機能します。

早期停止では、検証セットの選択も重要になります。検証セットは、学習セットのすべての点を代表するものでなければなりません。

ベイズ正則化を使用する場合には、収束に達するまでネットワークに学習させることが重要です。残差平方和、重み平方和、有効なパラメーターの数は、ネットワークが収束したときに一定の値になります。

早期停止と正則化の両方の手法において、いくつかの異なる初期条件からネットワークの学習を開始してみるのも良いでしょう。いずれかの手法が、特定の状況では失敗する可能性もあります。いくつかの初期条件でテストを行うことによって、ネットワーク性能がロバストであることを検証できます。

データセットが小規模で、関数近似ネットワークが学習中である場合、早期停止よりも、ベイズ正則化の方が汎化性能が良くなります。これは、ベイズ正則化では、検証データセットを学習データセットとは別のものにする必要がなく、すべてのデータを使用するためです。

アルゴリズムの性能について把握できるように、以下の表に示すいくつかのベンチマークデータセットについて、早期停止とベイズ正則化の両方のテストを行いました。

データセットのタイトル	点の数	ネットワーク	説明
BALL	67	2-10-1	ボール位置の測定値のデュアルセンサーキャリブレーション
SINE (5% N)	41	1-15-1	標準偏差 5% のガウスノイズを加えた 1 サイクルの正弦波
SINE (2% N)	41	1-15-1	標準偏差 2% のガウスノイズを加えた 1 サイクルの正弦波
ENGINE (ALL)	1199	2-30-2	エンジンセンサー (すべてのデータセット)
ENGINE (1/4)	300	2-30-2	エンジンセンサー (1/4 のデータセット)
CHOLEST (ALL)	264	5-15-3	コレステロール測定値 (すべてのデータセット)
CHOLEST (1/2)	132	5-15-3	コレステロール測定値 (1/2 のデータセット)

これらのデータセットのサイズはさまざまで、入力とターゲットの数が異なっています。これらのうち 2 つのデータセットでは、すべてのデータを使用してネットワークの学習を 1 回行い、その後でデータの一部のみを使用して、ネットワークの再学習を行いました。これにより、データセットを小さくしたときに、ベイズ正則化の有効性がどのようにより顕著になるのかが示されます。SINE データセットを除くすべてのデータセットは、物理システムから取得されています。これら 2 つは、1 サイクルの正弦波にさまざまなレベルのノイズを加えて、人工的に作成したものです。これらの 2 つのデータセットを使用したときのアルゴリズムの性能は、ノイズの影響を示しています。

次の表に、7 つのテストセットに対する早期停止 (ES) とベイズ正則化 (BR) の性能をまとめています (早期停止には trainscg アルゴリズムを使用しました。他のアルゴリズムも同様の性能が得られます)。

テストセットの平均二乗誤差

手法	BALL	ENGINE (ALL)	ENGINE (1/4)	CHOLEST (ALL)	CHOLEST (1/2)	SINE (5% N)	SINE (2% N)
ES	1.2e-1	1.3e-2	1.9e-2	1.2e-1	1.4e-1	1.7e-1	1.3e-1
BR	1.3e-3	2.6e-3	4.7e-3	1.2e-1	9.3e-2	3.0e-2	6.3e-3
ES/BR	92	5	4	1	1.5	5.7	21

ベイズ正則化は、ほとんどの場合に早期停止より性能が良いことがわかります。データセットが小規模なときや、データセットにわずかなノイズが含まれる場合には、性能の向上が顕著です。たとえば、BALL データセットはセンサーから取得されており、ごくわずかなノイズが含まれています。

ベイズ正則化による汎化性能は、多くの場合、早期停止より良くなりますが、必ずそうなるわけではありません。また、このツールボックスで実装されている形式のベイズ正則化では、パターン認識問題において、関数近似問題ほど良い性能は得られません。これは、ネットワーク出力が飽和している場合、レーベンバーグ・マルカート法アルゴリズムで使用されるヘッシアンの近似が、パターン認識問題の場合と比べてそれほど正確ではないためです。このほかにも、ベイズ正則化の手法は、一般的に早期停止よりも収束までに時間がかかるというデメリットもあります。

学習後の分析 (回帰)

学習済みネットワーク性能は、ある程度は学習セット、検証セット、テストセットに対する誤差で測定できますが、ネットワークの応答を詳しく調べると役に立つことがよくあります。選択肢の 1 つは、ネットワークの応答と対応するターゲット間で回帰分析を行うことです。ルーチン regression はこの分析を行うために設計されています。

次のコマンドは、学習済みネットワークに対して回帰分析を行う方法を説明するものです。

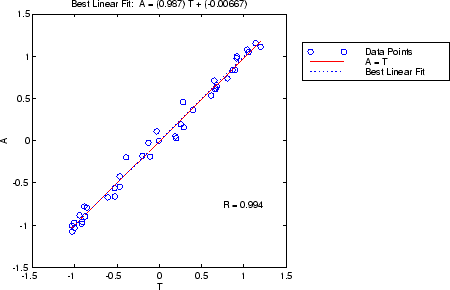
x = [-1:.05:1];
t = sin(2*pi*x)+0.1*randn(size(x));
net = feedforwardnet(10);
net = train(net,x,t);
y = net(x);
[r,m,b] = regression(t,y)

r =
    0.9935
m =
    0.9874
b =
   -0.0067

ネットワーク出力とそれに対応するターゲットを regression に渡します。3 つのパラメーターが返ります。最初の 2 つの m と b は、ターゲットをネットワーク出力に関連付ける最適線形回帰の勾配と y 切片に対応します。完全に近似している (出力がターゲットと完全に等しい) 場合は、勾配は 1 で、y 切片は 0 です。この例では、数値が非常に近いことがわかります。regression によって返される 3 つ目の変数は、出力とターゲットの相関係数 (R 値) です。これは、出力の変動がターゲットによってどの程度説明されるかを示す尺度となります。この数値が 1 に等しければ、ターゲットと出力には完全な相関があります。この例では、数値は 1 に非常に近く、よく近似していることを示しています。

次の図は、regression で得られるグラフィックス出力を示したものです。ネットワーク出力は、ターゲットに対して丸印でプロットされます。最適な線形近似は、破線で示されています。完全な近似 (出力とターゲットが等しい) は、実線で示されています。この例では、近似が非常に良いため、最適線形近似の線と完全な近似の線を区別することが困難です。

Outputs versus targets with lines showing the best linear fit and the perfect fit.