シグモイドモデルの当てはめ

シグモイドモデルは、用量反応曲線や個体群ダイナミクスのモデル化によく使用される S 字型の曲線です。これらのモデルは、多くの人工ニューラルネットワークで活性化関数としても使用されています。Curve Fitting Toolbox™ は、次の方程式をもつロジスティック、4 パラメーターロジスティック、ゴンペルツのシグモイドモデルをサポートしています。

シグモイドモデル	方程式
ロジスティック	$f (x) = \frac{a}{1 + e^{- b (x - c)}}$
4 パラメーターロジスティック	$f (x) = d + \frac{a - d}{1 + {(\frac{x}{c})}^{b}}$
ゴンペルツ	$f (x) = d + (a - d) e^{- e^{- b (x - c)}}$

これらの方程式で、a と d は水平方向の漸近線のパラメーター、b は増加率のパラメーターです。4 パラメーターロジスティックモデルでは、入力データ x に含まれる要素はすべて正であるかすべて負でなければならず、c は水平方向の漸近線間の中間点です。ゴンペルツモデルの c は曲線の変曲点です。ロジスティックモデルの c は中間点であり、変曲点でもあります。

曲線フィッターアプリを使用したシグモイドモデルの当てはめ

ライブスクリプトを開く

linspace、exp、およびrandn関数と標準ロジスティック関数 $p (x) = \frac{1}{1 + e^{- x}}$ を使用して、ノイズを追加したデータを生成します。"p" は、0 から 1 までの範囲で、入力 "x" が与えられたときに事象が発生する確率を表します。

rng(0,"twister") %  For reproducibility
x = linspace(-5,5,100)';
p = 1./(1+exp(-x)) + 0.02*randn(100,1);
p(p>1) = 1;
p(p<0) = 0;

コマンドラインから曲線フィッターアプリを開きます。

curveFitter

または、[アプリ] タブで、アプリギャラリーの [数学、統計および最適化] グループにある [曲線フィッター] をクリックします。

アプリで、近似のデータ変数を選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] の値として x、[Y データ] の値として p を選択します。

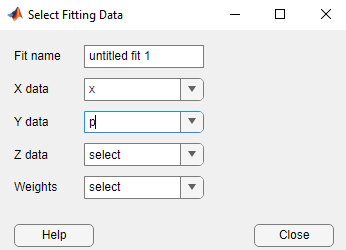
変数を選択すると、アプリによってデータ点がプロットされます。既定では、アプリは線形多項式をデータに当てはめます。シグモイドモデルを当てはめるには、[曲線フィッター] タブの [近似タイプ] ギャラリーで Sigmoidal をクリックします。

既定では、アプリはロジスティックモデルをプロットします。

プロットは、ロジスティック近似が大部分のデータに追従していることを示しています。x が負の値のときは確率が小さく、その後は増加して、1 の近くで横ばいになります。[近似テーブル] に、ロジスティックモデルの適合度の統計量が表示されます。たとえば、誤差二乗和 (SSE) は約 0.048、決定係数の値は約 1 です。また、[結果] ペインに、モデル方程式、および 95% 信頼限界の近似係数が表示されます。

別のモデル方程式を使用するには、[近似オプション] ペインの [モデル] メニューから別のモデル名を選択します。たとえば、ゴンペルツモデルを選択できます。

プロットは、ゴンペルツ曲線の下側の漸近線がゼロより大きいことを示しています。[近似テーブル] は、この近似はロジスティック近似に比べて SSE の値が大きく、決定係数の値がわずかに小さいことを示しています。この結果は、データがロジスティック関数ではなくゴンペルツ関数から生成されていることによるものです。

コマンドラインでのシグモイドモデルの当てはめ

ライブスクリプトを開く

linspace、tanh、およびrandn関数を使用して、ノイズを追加したデータを生成します。

rng(0,"twister") %  For reproducibility
pts = linspace(-5,5,100)';
x = linspace(1,11,100)';
y = tanh(pts)+0.1*randn(100,1);

ベクトル x には独立変数のデータが格納され、ベクトル y には従属変数のデータが格納されます。

scatter関数を使用して、x と y のデータの散布図を作成します。

scatter(x,y)

Figure contains an axes object. The axes object contains an object of type scatter.

散布図は、y には正の値と負の値が含まれ、x に含まれる値はすべて正であり、データが S 字型になることを示しています。

4 パラメーターロジスティックモデルを x と y に当てはめます。

f = fit(x,y,'logistic4')

f = 
     General model Logistic4:
     f(x) = d + (a-d)/(1 + (x/c)^b)
     Coefficients (with 95% confidence bounds):
       a =     -0.9507  (-0.989, -0.9125)
       b =       12.93  (11.14, 14.72)
       c =       6.013  (5.94, 6.086)
       d =       1.003  (0.9608, 1.046)

f は、データに 4 パラメーターロジスティックモデルを当てはめた結果を含むcfitオブジェクトです。

f を x および y と一緒にプロットします。

plot(f,x,y)

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fitted curve.

プロットは、近似曲線 f が大部分のデータに追従していることを示しています。

参照

[1] Tjørve, Kathleen M. C., and Even Tjørve. “The Use of Gompertz Models in Growth Analyses, and New Gompertz-Model Approach: An Addition to the Unified-Richards Family.” PLOS ONE, edited by Roeland M.H. Merks, vol. 12, no. 6, June 2017, p. e0178691. DOI.org (Crossref), https://doi.org/10.1371/journal.pone.0178691.

参考