Curve Fitting Toolbox による内挿
"内挿" は既知のデータ点間に位置する値を推定するプロセスです。
内挿は、すべての i について、与えられたデータ サイト xi において与えられたデータ値 yi に一致する関数 f (ここで、f(xi) = yi) の作成を必要とします。
ほとんどの内挿法は、内挿 f を次の式の一意の関数として作成します。
ここで、関数 fj の形式は内挿法によって異なります。
スプライン内挿の場合、fj は n 個の連続 B スプライン Bj(x) = B(x|tj,...,tj+k), j = 1:n (ノット シーケンス t1 ≤ t2 ≤ ... ≤ tn + k の場合に次数 k) になります。
内挿法について
Curve Fitting Toolbox™ は、以下の表に説明する内挿法をサポートします。
手法 | 説明 |
|---|---|
最近傍 | 最近傍内挿。この手法では、内挿される点の値を最も近いデータ点の値に設定します。 |
線形 | 線形内挿。この手法では、曲線のデータの各 2 点間または曲面の各 3 点間を異なる線形多項式で近似します。 |
自然近傍 | 自然近傍内挿。この手法では、内挿される点の値を最も近いデータ点の加重平均に設定します。内挿曲面はサンプル点以外の場所では C1 連続です。 |
形状維持 (PCHIP) | 区分的 3 次エルミート内挿 (PCHIP)。この手法では、データの単調性と形状が維持されます (曲線についてのみ)。 |
3 次スプライン | 3 次スプライン内挿。この手法では、曲線のデータの各 2 点間または曲面の各 3 点間に異なる 3 次多項式を使って当てはめます。 |
重調和 (v4) | MATLAB® 4 |
薄板スプライン | 薄板スプライン内挿。この手法は、適切に外挿することもできる滑らかな曲面を当てはめます (曲面についてのみ)。 |
内挿曲面近似では、線形法、最近傍法、自然近傍法には MATLAB 関数 scatteredInterpolant が使用され、3 次スプライン法と重調和法には MATLAB 関数 griddata が使用されます。薄板スプライン法では関数 tpaps を使用します。
使用する内挿法は、近似データの特性、曲線に求める滑らかさ、速度の考慮、近似後の解析の要件などの要素により異なります。線形法および最近傍法はモデルを効率的に当てはめられますが、結果として得られる曲線はあまり滑らかではありません。自然近傍法、3 次スプライン法、形状維持法、重調和法は、モデルの近似に要する時間が長くなりますが、結果として得られる曲線は非常に滑らかです。
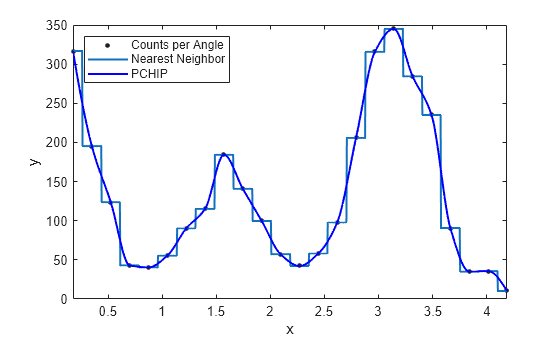
例として、以下のプロットに、carbon12alpha.mat サンプル データセットの核反応データに対する最近傍内挿近似と形状維持 (PCHIP) 内挿近似を示します。最近傍内挿は、形状維持内挿ほど滑らかではありません。

メモ:
内挿では適合度の統計量、予測限界、重みは定義されません。また、内挿はデータ点を通過するため、近似の残差は (コンピューター精度の範囲内で) 常に 0 です。
重調和内挿近似は、放射基底関数内挿で構成されます。Curve Fitting Toolbox がサポートする他の内挿はすべて "区分的多項式" であり、これはデータ点間で定義される複数の多項式で構成されます。3 次スプラインおよび PCHIP 内挿の場合、4 つの係数は各区分を記述します。Curve Fitting Toolbox は 3 次多項式を使用してその 4 つの係数を計算します。詳細については、以下を参照してください。
3 次スプライン内挿については、
spline形状維持 (PCHIP) 内挿について、および PCHIP と 3 次スプライン内挿の比較については、
pchip曲面内挿については、
scatteredInterpolant、griddata、tpapsデータ点数より次数が 1 小さい単一の多項式内挿を使ってデータに当てはめることができます。しかし、そのような近似のデータ点間での振る舞いは予測できません。低次セグメントをもつ区分的多項式は近似データ領域から大きくずれないので、より広範なデータ セットの分析に役立ちます。
内挿近似の選択
内挿近似の対話的な選択
MATLAB コマンド ラインで curveFitter と入力して曲線フィッター アプリを開きます。または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。
[曲線フィッター] タブの [近似タイプ] セクションで [内挿] 近似を選択します。アプリによって、すべてのデータ点を通過する内挿曲線または内挿曲面が当てはめられます。
[近似オプション] ペインで、[内挿法] の値を指定できます。

曲線データの場合、[内挿法] は Linear、Nearest neighbor、Cubic spline、または Shape-preserving (PCHIP) に設定できます。曲面データの場合、[内挿法] は Linear、Nearest neighbor、Natural neighbor、Cubic spline、Biharmonic (v4)、または Thin-plate spline に設定できます。
曲面の場合、内挿近似では、Linear、Nearest neighbor、Natural neighbor の手法には関数 scatteredInterpolant、Cubic Spline と Biharmonic (v4) の手法には関数 griddata、Thin-plate spline の手法には関数 tpaps が使用されます。滑らかな曲面の内挿と適切な外挿特性の両方が必要なときは、Thin-plate spline メソッドを試してください。
ヒント
データ変数間のスケールが大きく異なる場合は、[データのセンタリングとスケーリング] チェック ボックスをオフにして近似の違いを確認してください。入力の正規化は、区分的な Linear と Cubic Spline の内挿法、および Nearest neighbor と Natural neighbor の曲面内挿法の結果に影響する場合があります。
関数 fit を使用した線形内挿モデルによる近似
census サンプル データ セットを読み込みます。
load census変数 pop と cdate には、人口サイズと国勢調査の実施年に関するデータがそれぞれ含まれています。
関数fitを使用して、内挿モデルの名前に説明されている内挿モデルのいずれかを当てはめることができます。ここでは、'linearinterp' オプションを使用して線形内挿モデルを当てはめ、結果をプロットします。
f = fit(cdate,pop,'linearinterp');
plot(f,cdate,pop);
線形内挿モデルの比較
carbon12alpha サンプル データ セットを読み込みます。'nearestinterp' オプションと 'pchip' オプションを使用して、最近傍と PCHIP 両方の内挿近似を作成します。
load carbon12alpha f1 = fit(angle,counts,'nearestinterp'); f2 = fit(angle,counts,'pchip');
近似曲線 f1 と f2 を同じ Figure にプロットして比較します。
p1 = plot(f1,angle,counts); xlim([min(angle),max(angle)]) hold on p2 = plot(f2,'b'); hold off legend([p1;p2],'Counts per Angle','Nearest Neighbor','PCHIP',... 'Location','northwest')