受動性インデックス

この例は、線形時不変システムの受動性のさまざまな測定値の計算方法を示します。

受動システム

線形システム G(s) は、すべての I/O 軌跡 $$(u(t),y(t))$$ が次を満たす場合に受動的です。

$${\int }_0^T{y}^T(t)u(t)dt>0,\forall T>0$$

ここで、$$y^T(t)$$ は $$y(t)$$ の転置を表します。

システムが "どれだけ受動的であるか" を測定するために、受動性インデックスを使用します。

• 入力受動性インデックスは次を満たす最大の $$\nu$$ として定義される

$${\int }_0^T{y}^T(t)u(t)dt>\nu {\int }_0^T{u}^T(t)u(t)dt$$

$$\nu >0$$ のとき、システム G は "入力で厳密に受動的" (ISP) です。$$\nu$$ は "入力フィードフォワード受動性" (IFP) インデックスとも呼ばれ、システムを受動的にするために必要な最小のフィードフォワード アクションに相当します。

• 出力受動性インデックスは次を満たす最大の $$\rho$$ として定義される

$${\int }_0^T{y}^T(t)u(t)dt>\rho {\int }_0^T{y}^T(t)y(t)dt$$

$$\rho >0$$ のとき、システム G は "出力で厳密に受動的" (OSP) です。$$\rho$$ は "出力フィードバック受動性" (OFP) インデックスとも呼ばれ、システムを受動的にするために必要な最小のフィードバック アクションに相当します。

• I/O 受動性インデックスは次を満たす最大の $$\tau$$ として定義される

$${\int }_0^T{y}^T(t)u(t)dt>\tau {\int }_0^T(u^T(t)u(t)+y^T(t)y(t))dt$$

$$\tau >0$$ のとき、システムは "非常に厳密に受動的" (VSP) です。

回路の例

次の例を考えます。電流 $$I$$ を入力、電圧 $$V$$ を出力とします。キルヒホッフの電圧則および電流則に基づき、$$G(s)$$ について次の伝達関数を得ます。

$$G(s)=\frac{V(s)}{I(s)}=\frac{(Ls+R)(Rs+\frac{1}{C})}{L{s}^2+2Rs+\frac{1}{C}}.$$

$$R=2$$、$$L=1$$、および $$C=0.1$$ とします。

R = 2; L = 1; C = 0.1; 
s = tf('s');
G = (L*s+R)*(R*s+1/C)/(L*s^2 + 2*R*s+1/C);

isPassive を使用して $$G(s)$$ が受動的であるかどうかを確認します。

PF = isPassive(G)

PF = logical
   1

PF = true であるため、$$G(s)$$ は受動的です。getPassiveIndex を使用して $$G(s)$$ の受動性インデックスを計算します。

% Input passivity index
nu = getPassiveIndex(G,'in')

nu = 
2

% Output passivity index
rho = getPassiveIndex(G,'out')

rho = 
0.2857

% I/O passivity index
tau = getPassiveIndex(G,'io')

tau = 
0.2642

$$\tau >0$$ であるため、システム $$G(s)$$ は非常に厳密に受動的です。

周波数領域の特性

線形システムは、次のように "正の実数" である場合にのみ受動的です。

$$G(j\omega )+G^H(j\omega )>0\forall \omega \in R.$$

左辺の最小の固有値は、入力受動性インデックス $$\nu$$ に関連しています。

$$\nu =\frac{1}{2}\underset{\omega }{\min }{\lambda }_{\min }(G(j\omega )+G^H(j\omega ))$$

ここで、$${\lambda }_{\min }$$ は最小の固有値を表します。同様に、$$G(s)$$ が最小位相のとき、出力受動性インデックスは次で与えられます。

$$\rho =\frac{1}{2}\underset{\omega }{\min }{\lambda }_{\min }(G^{-1}(j\omega )+G^{-H}(j\omega )).$$

回路の例でこれを検証します。回路の伝達関数のナイキスト線図をプロットします。

nyquist(G)

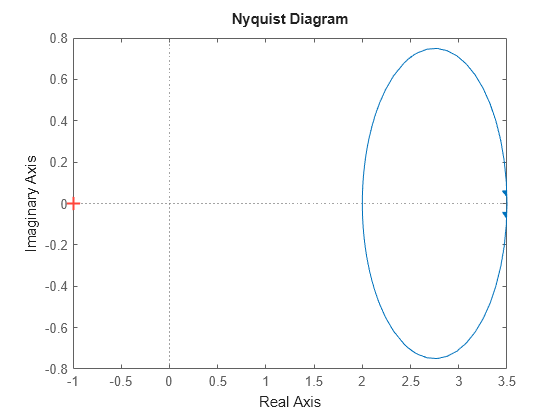
ナイキスト線図全体が右半平面にあるため、$$G(s)$$ は正の実数です。ナイキスト曲線で一番左の点は $$(x,y)=(2,0)$$ なので、入力受動性インデックスは $$\nu =2$$ であり、前に取得した値と同じです。同様に、$$G^{-1}(s)$$ のナイキスト曲線で一番左の点により、出力受動性インデックス値 $$\rho =0.286$$ が与えられます。

相対受動性インデックス

次の "正の実数" 条件

$$G(j\omega )+G^H(j\omega )>0\forall \omega \in R$$

が、次のスモール ゲイン条件と同等であることを示せます。

$$||(I-G(j\omega ))(I+G(j\omega ){)}^{-1}||<1\forall \omega \in R.$$

相対受動性インデックス (R インデックス) は、$$I+G$$ が最小位相のとき $$(I-G)(I+G{)}^{-1}$$ の周波数についてのピーク ゲインであり、それ以外の場合は $$+\infty$$ です。

$$R={\Vert (I-G)(I+G{)}^{-1}\Vert }_{\infty }.$$

時間領域の場合、R インデックスは次を満たす最小の $$r>0$$ です。

$${\int }_0^T||y-u|{|}^{2}dt<r^2{\int }_0^T||y+u|{|}^{2}dt$$.

システム $$G(s)$$ は $$R<1$$ の場合にのみ受動的になり、$$R$$ が小さいほどシステムはより受動的になります。getPassiveIndex を使用して回路の例の R インデックスを計算します。

R = getPassiveIndex(G)

R = 
0.5556

結果の $$R$$ 値は、回路が極めて受動的なシステムであることを示します。

参照

[1] Xia, M., P. Gahinet, N. Abroug, C. Buhr, and E. Laroche. “Sector Bounds in Stability Analysis and Control Design.” International Journal of Robust and Nonlinear Control 30, no. 18 (December 2020): 7857–82. https://doi.org/10.1002/rnc.5236.

参考

getPassiveIndex | isPassive

トピック

• 受動性および受動性インデックスについて
• 受動システムの並列相互接続
• 受動システムの直列相互接続
• 受動システムのフィードバック相互接続