受動システムの直列相互接続
この例では、受動システムの直列相互接続のプロパティについて説明します。
受動システムの直列相互接続
2 つのサブシステム と の直列の相互接続について考えます。相互接続されたシステム は入力 から出力 へのマッピングで指定されます。
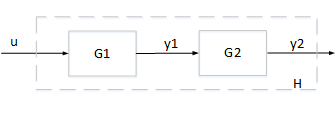
並列相互接続やフィードバック相互接続とは対照的に、サブシステム と の受動性は相互接続されたシステム の受動性を保証しません。以下に例を示します。
次で確認されるとおり、両方のシステムは受動的です。
G1 = tf([5 3 1],[1,2,1]); isPassive(G1)
ans = logical
1
G2 = tf([1,1,5,.1],[1,2,3,4]); isPassive(G2)
ans = logical
1
しかし、 と の直列相互接続は受動的ではありません。
H = G2*G1; isPassive(H)
ans = logical
0
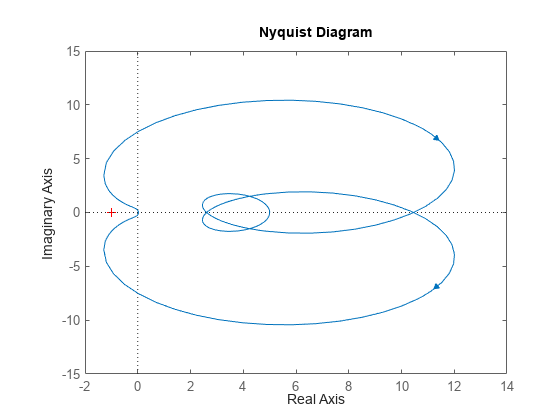
これは、 のナイキスト線図が正の実数ではないことを検証して確認されます。
nyquist(H)
直列相互接続の受動性インデックス
受動システムの直列相互接続は一般的に受動的ではありませんが、 と の受動性インデックスと、 の受動性インデックスとの間には関係性があります。 と で と の入力受動性インデックスを表し、 と で出力受動性インデックスを表します。これらすべてのインデックスが正の場合、直列相互接続 の入力受動性インデックス と出力受動性インデックス は次を満たします。
つまり、 の入力または出力における受動性の不足は、右辺の式を下回りません。詳細については、Arcak, M. および Sontag, E.D. による論文 "Diagonal stability of a class of cyclic systems and its connection with the secant criterion," Automatica, Vol 42, No. 9, 2006, pp. 1531-1537. を参照してください。上記の例でこれらの下限を確認します。
% Output passivity index for G1 rho1 = getPassiveIndex(G1,'output'); % Output passivity index for G2 rho2 = getPassiveIndex(G2,'output'); % Input passivity index for H=G2*G1 nu = getPassiveIndex(H,'input')
nu = -1.2886
% Lower bound
-0.125/(rho1*rho2)ans = -2.4194
同様に、 の出力受動性インデックスの下限を確認します。
% Input passivity index for G1 nu1 = getPassiveIndex(G1,'input'); % Input passivity index for G2 nu2 = getPassiveIndex(G2,'input'); % Output passivity index for H=G2*G1 rho = getPassiveIndex(H,'output')
rho = -0.6966
% Lower bound
-0.125/(nu1*nu2)ans = -6.0000