受動システムのフィードバック相互接続

この例では、受動システムのフィードバック相互接続のプロパティについて説明します。

受動システムのフィードバック相互接続

2 つのサブシステム $$G_1$$ と $$G_2$$ のフィードバックでの相互接続について考えます。相互接続されたシステム $$H$$ は入力 $$r$$ を出力 $$y_1$$ にマッピングします。

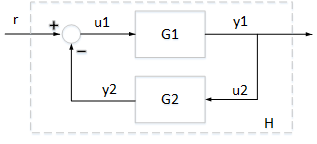
システム $$G_1$$ と $$G_2$$ がともに受動的である場合、相互接続されたシステム $$H$$ は受動的となることが保証されます。たとえば次の場合

$$G_1(s)=\frac{s^2+s+1}{s^2+s+4},G_2(s)=\frac{s+2}{s+5}.$$

次で確認されるとおり、両方のシステムは受動的です。

G1 = tf([1,1,1],[1,1,4]); 
isPassive(G1)

ans = logical
   1

G2 = tf([1,2],[1,5]);
isPassive(G2)

ans = logical
   1

したがって、相互接続されたシステムは受動的です。

H = feedback(G1,G2);
isPassive(H)

ans = logical
   1

これは、$$H$$ のナイキスト線図が正の実数であることを検証して確認されます。

nyquist(H)

フィードバック相互接続の受動性インデックス

$$G_1$$ と $$G_2$$ の受動性インデックスと、相互接続されたシステム $$H$$ の受動性インデックスとの間には関係性があります。$${\nu }_1$$ と $${\nu }_2$$ で $$G_1$$ と $$G_2$$ の入力受動性インデックスを表し、$${\rho }_1$$ と $${\rho }_2$$ で出力受動性インデックスを表します。すべてのインデックスが正の場合、フィードバック相互接続 $$H$$ の入力受動性インデックス $$\nu$$ と出力受動性インデックス $$\rho$$ は次を満たします。

$$\nu \ge \frac{{\nu }_1{\rho }_2}{{\nu }_1+{\rho }_2},\rho \ge {\rho }_1+{\nu }_2.$$

つまり、$$G_1$$ と $$G_2$$ の入出力受動性インデックスから、閉ループ システム $$H$$ の最小レベルの入出力受動性を一部推測できます。詳細については、Zhu, F.、Xia, M および Antsaklis, P.J. による論文 "Passivity analysis and passivation of feedback systems using passivity indices," American Control Conference , 2014, pp. 1833-1838. を参照してください。入力受動性インデックス $$\nu$$ の下限を確認します。

% Input passivity index for G1
nu1 = getPassiveIndex(G1,'input');
% Output passivity index for G2
rho2 = getPassiveIndex(G2,'output');
% Input passivity index for H
nu = getPassiveIndex(H,'input')

nu = 0.1293

% Lower bound
nu1*rho2/(nu1+rho2)

ans = 7.1402e-11

同様に、$$H$$ の出力受動性インデックスの下限を確認します。

% Output passivity index for G1
rho1 = getPassiveIndex(G1,'output');
% Input passivity index for G2
nu2 = getPassiveIndex(G2,'input');
% Output passivity index for H
rho = getPassiveIndex(H,'output')

rho = 0.4441

% Lower bound
rho1+nu2

ans = 0.4000

参考

getPassiveIndex | isPassive

関連するトピック

• 受動性および受動性インデックスについて
• 受動システムの並列相互接続
• 受動システムの直列相互接続
• 通信遅延での受動制御

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい