Main Content

通信遅延での受動制御

この例では次を使用します。

スクリプトを開く

この例では、受動制御システムで通信遅延を緩和する方法について説明します。

受動性ベースの制御

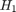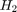受動性定理により、2 つの厳密に受動的なシステム $H_1$ および $H_2$ の負のフィードバック相互接続は常に安定します。

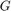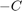物理プラントが受動である場合は、ロバスト性と安全性の理由から受動コントローラーを使用した方が有利です。ただし、ネットワーク化された制御システムでは、通信遅延によって受動性ベースの制御の利点が打ち消され、不安定になる可能性があります。この点を説明するために、「柔軟ビームの振動制御」の例で取り上げたプラントと 2 次受動コントローラーを使用します。基になる制御の問題の背景についてはこの例を参照してください。プラント モデル $G$ と受動コントローラー $C$ ($C$ は他の例の $-C$ に対応) を読み込みます。

load BeamControl G C

bode(G,C,{1e-2,1e4})
legend('G','C')

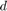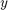制御構成と、$d$ から $y$ へのインパルス応答を以下に示します。

impulse(feedback(G,C))

通信遅延の不安定化の影響

ここでは、センサーとコントローラーの間およびコントローラーとアクチュエータの間に相当の通信遅延があることを前提にします。この状況は、Simulink で次のようにモデル化されます。

open_system('DelayedFeedback')

通信遅延は次のように設定されます。

T1 = 1;
T2 = 2;

このモデルをシミュレーションすると、通信遅延によってフィードバック ループが不安定になることがわかります。

散乱変換

遅延の影響を緩和するためには、ネットワーク上でプラントとコントローラー間で交換される信号の単純な線形変換を使用します。

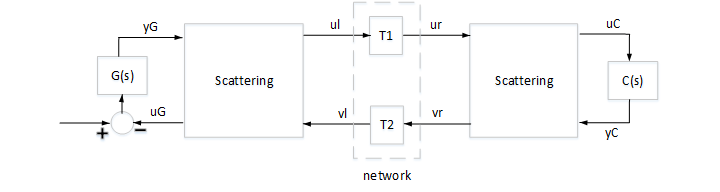
図 1: ネットワーク化された制御システム

これは、"散乱変換" と呼ばれ、次の式によって求められます。

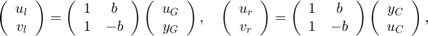
$$ \left(\begin{array}{c}u_l\\v_l\end{array}\right) =
 \left(\begin{array}{cc}1 & b \\ 1 & -b \end{array}\right)
 \left(\begin{array}{c}u_G\\y_G\end{array}\right) , \quad
 \left(\begin{array}{c}u_r\\v_r\end{array}\right) =
 \left(\begin{array}{cc}1 & b \\ 1 & -b \end{array}\right)
 \left(\begin{array}{c}y_C\\u_C\end{array}\right) , $$

これは、次の関数と等価です。

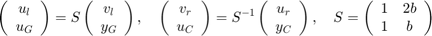
$$ \left(\begin{array}{c}u_l\\u_G\end{array}\right) = S
 \left(\begin{array}{c}v_l\\y_G\end{array}\right) , \quad
 \left(\begin{array}{c}v_r\\u_C\end{array}\right) = S^{-1}
 \left(\begin{array}{c}u_r\\y_C\end{array}\right) , \quad
 S = \left(\begin{array}{cc}1 & 2b \\ 1 & b \end{array}\right) $$

ここで、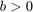$b>0$ です。遅延がない場合、2 つの散乱変換は相殺し合い、図 1 のブロック線図は、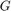$G$ および $C$ の負のフィードバック相互接続と等価になることに注意してください。

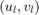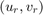ただし、遅延がある場合、$(u_l,v_l)$ は $(u_r,v_r)$ と同等ではなくなり、この散乱変換によって閉ループ システムのプロパティが変わります。実際、次であること、

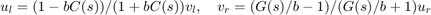
$$ u_l = (1-bC(s))/(1+bC(s)) v_l , \quad
 v_r = (G(s)/b-1)/(G(s)/b+1) u_r $$

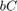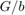および $bC$ と $G/b$ の厳密な受動性が確認されると、次のようになります。

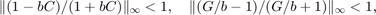
$$ \| (1-bC)/(1+bC) \|_\infty < 1 , \quad \| (G/b-1)/(G/b+1) \|_\infty <&#10;1 , $$

スモール ゲイン定理により、遅延がどれだけ大きくても図 1 のフィードバック相互接続は常に安定することが保証されます。これを確認するには、値 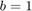$b=1$ に対して図 1 のブロック線図の Simulink モデルを作成します。

b = 1;

open_system('ScatteringTransformation')

以前実行したように閉ループ システムのインパルス応答をシミュレートします。応答は安定し、大きな遅延がありながらも遅延のない応答と同様になりました。

散乱変換の詳細については、T. Matiakis、S. Hirche および M. Buss 著の「Independent-of-Delay Stability of Nonlinear Networked Control Systems by Scattering Transformation」 (『Proceedings of the 2006 American Control Conference』 (2006 年) p 2801 ～ 2806) を参照してください。

参考

|

関連する例

詳細