柔軟ビームの振動制御
この例では、柔軟ビームの振動を低減するためにコントローラーを調整する方法を説明します。
柔軟ビームのモデル
図 1 は、柔軟ビームのアクティブな振動制御システムを示しています。

図 1: 柔軟ビームのアクティブ制御
この設定では、力  を提供するアクチュエータと速度センサーが併置されています。有限要素解析を使用して、制御入力
を提供するアクチュエータと速度センサーが併置されています。有限要素解析を使用して、制御入力  から速度
から速度  への伝達関数をモデル化できます。最初の 6 つのモードのみを維持して、次の形式のプラント モデルを取得します。
への伝達関数をモデル化できます。最初の 6 つのモードのみを維持して、次の形式のプラント モデルを取得します。
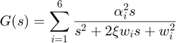
この場合、次のパラメーター値を使用します。
% Parameters
xi = 0.05;
alpha = [0.09877, -0.309, -0.891, 0.5878, 0.7071, -0.8091];
w = [1, 4, 9, 16, 25, 36];
 の結果のビーム モデルは次の式で表されます。
の結果のビーム モデルは次の式で表されます。
% Beam model G = tf(alpha(1)^2*[1,0],[1, 2*xi*w(1), w(1)^2]) + ... tf(alpha(2)^2*[1,0],[1, 2*xi*w(2), w(2)^2]) + ... tf(alpha(3)^2*[1,0],[1, 2*xi*w(3), w(3)^2]) + ... tf(alpha(4)^2*[1,0],[1, 2*xi*w(4), w(4)^2]) + ... tf(alpha(5)^2*[1,0],[1, 2*xi*w(5), w(5)^2]) + ... tf(alpha(6)^2*[1,0],[1, 2*xi*w(6), w(6)^2]); G.InputName = 'uG'; G.OutputName = 'y';
このセンサーとアクチュエータの構成では、ビームは次の受動システムになります。
isPassive(G)
ans = logical 1
これは、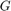 のナイキスト線図が正の実数であることを観測して確認されます。
のナイキスト線図が正の実数であることを観測して確認されます。
nyquist(G)

LQG コントローラー
LQG 制御は、アクティブ振動制御の自然な形式です。LQG 制御の設定を図 2 に示します。信号 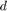 および
および  は、それぞれプロセス ノイズと測定ノイズです。
は、それぞれプロセス ノイズと測定ノイズです。

図 2: LQG 制御構造
まず lqg を使用して、次の目的に最適な LQG コントローラーを計算します。
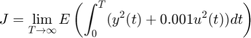
ここでは、次のノイズ分散を使用します。
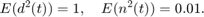
[a,b,c,d] = ssdata(G);
M = [c d;zeros(1,12) 1]; % [y;u] = M * [x;u]
QWV = blkdiag(b*b',1e-2);
QXU = M'*diag([1 1e-3])*M;
CLQG = lqg(ss(G),QXU,QWV);
LQG 最適コントローラー CLQG は 12 の状態と、ノッチとなる複数の零点をもつ複雑なコントローラーです。
size(CLQG)
State-space model with 1 outputs, 1 inputs, and 12 states.
bode(G,CLQG,{1e-2,1e3}), grid, legend('G','CLQG')

汎用の調整器 systune を使用してこのコントローラーの簡略化を試行します。systune では、最大次数のコントローラーに制限されることはなく、どの次数のコントローラーでも調整できます。この例では、2 次状態空間コントローラーを調整します。
C = ltiblock.ss('C',2,1,1);
図 2 のブロック線図の閉ループ モデルを構築します。
C.InputName = 'yn'; C.OutputName = 'u'; S1 = sumblk('yn = y + n'); S2 = sumblk('uG = u + d'); CL0 = connect(G,C,S1,S2,{'d','n'},{'y','u'},{'yn','u'});
上記の LQG 基準 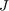 を単独の調整目標として使用します。LQG 調整目標では、性能の重みとノイズ共分散を直接指定できます。
を単独の調整目標として使用します。LQG 調整目標では、性能の重みとノイズ共分散を直接指定できます。
R1 = TuningGoal.LQG({'d','n'},{'y','u'},diag([1,1e-2]),diag([1 1e-3]));
次に、コントローラー C を調整して LQG 目的 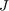 を最小化します。
を最小化します。
[CL1,J1] = systune(CL0,R1);
Final: Soft = 0.478, Hard = -Inf, Iterations = 40
オプティマイザーが 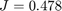 の 2 次コントローラーを検出しました。
の 2 次コントローラーを検出しました。CLQG の最適な 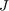 値と比較します。
値と比較します。
[~,Jopt] = evalGoal(R1,replaceBlock(CL0,'C',CLQG))
Jopt =
0.4673
性能低下は 5% 未満で、コントローラーの複雑度を 12 から 2 状態へ低減しました。さらに、2 つのコントローラーの 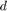 から
から  へのインパルス応答を比較します。2 つの応答はほぼ同じです。したがって、シンプルな 2 次コントローラーで最適に近い振動減衰を得ることができます。
へのインパルス応答を比較します。2 つの応答はほぼ同じです。したがって、シンプルな 2 次コントローラーで最適に近い振動減衰を得ることができます。
T0 = feedback(G,CLQG,+1); T1 = getIOTransfer(CL1,'d','y'); impulse(T0,T1,5) title('Response to impulse disturbance d') legend('LQG optimal','2nd-order LQG')

受動 LQG コントローラー
ビームの近似モデルを使用してこれら 2 つのコントローラーを設計しました。推測的に、これらのコントローラーが実際のビームで良好に動作するという保証はありません。ただし、ビームは受動物理システムであり、受動システムの負のフィードバック相互接続は常に安定することはわかっています。したがって、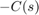 が受動的である場合、閉ループ システムが安定することは確信できます。
が受動的である場合、閉ループ システムが安定することは確信できます。
最適な LQG コントローラーは受動ではありません。実際、 は最小位相ですらないため、その相対受動インデックスは無限です。
は最小位相ですらないため、その相対受動インデックスは無限です。
getPassiveIndex(-CLQG)
ans = Inf
これはナイキスト線図によって確認されます。
nyquist(-CLQG)

systune を使用すると、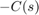 が受動的でなければならないという追加の要件によって 2 次コントローラーを再調整できます。これを行うには、
が受動的でなければならないという追加の要件によって 2 次コントローラーを再調整できます。これを行うには、yn から u への開ループ伝達関数 ( ) に対する受動性調整目標を作成します。"WeightedPassivity" 目標を使用してマイナス記号を考慮します。
) に対する受動性調整目標を作成します。"WeightedPassivity" 目標を使用してマイナス記号を考慮します。
R2 = TuningGoal.WeightedPassivity({'yn'},{'u'},-1,1);
R2.Openings = 'u';
今度は閉ループ モデル CL1 を再調整して、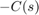 を受動にすることを条件に LQG 目的
を受動にすることを条件に LQG 目的 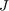 を最小化します。ここでは受動性目標
を最小化します。ここでは受動性目標 R2 が厳密な制約として指定されていることに注意してください。
[CL2,J2,g] = systune(CL1,R1,R2);
Final: Soft = 0.478, Hard = 1, Iterations = 37
調整器は前と同様に 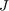 値を達成し、受動性を適用します (1 未満という厳密な制約)。
値を達成し、受動性を適用します (1 未満という厳密な制約)。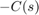 が受動的であることを確認します。
が受動的であることを確認します。
C2 = getBlockValue(CL2,'C');
passiveplot(-C2)

LQG 最適コントローラーの改善が最もよく確認できるのは、ナイキスト線図です。
nyquist(-CLQG,-C2) legend('LQG optimal','2nd-order passive LQG')

最後に、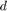 から
から  へのインパルス応答を比較します。
へのインパルス応答を比較します。
T2 = getIOTransfer(CL2,'d','y'); impulse(T0,T2,5) title('Response to impulse disturbance d') legend('LQG optimal','2nd-order passive LQG')

systune を使用して、ほぼ最適な LQG 性能の 2 次受動コントローラーを設計しました。
参考
systune | TuningGoal.WeightedPassivity | TuningGoal.LQG