跳ねるボールの LPV モデル

この例では、lpvss を使用して、マルチモードダイナミクスを示すシステムの線形パラメーター変動 (LPV) 表現を構成する方法を説明します。

このシステムのダイナミクスは関数 BouncingBallDF で定義されています。このモデルの詳細については、LTI 配列を使用したマルチモードダイナミクスのシミュレーションを参照してください。

非圧縮時のバネの長さ a1 と a2 および初期の質量の高さ h1 と h2 を定義します。

a1 = 12;    % uncompressed length of spring 1 (mm)
a2 = 20;    % uncompressed length of spring 2 (mm)
h1 = 100;   % initial height of mass m1 (mm)
h2 = a2;    % initial height of mass m2 (mm)

中程度の床剛性

最初に、2 番目の質量 k2 のバネ定数を 300 g/s^2 に設定して、柔らかい表面に対する応答をシミュレートします。状態は $x = [y_{1}, {\dot{y}}_{1}, y_{2}, {\dot{y}}_{2}]$ です。

入力は定数 $u$ = 1 (強制項は $F = mgu$ ) です。

k2 = 300;   % spring constant for second mass (g/s^2)
sys = lpvss("ygap",@(t,p) BouncingBallDF(t,p,k2)); % p = ygap = y1-y2

t = 0:0.05:40;
pFcn = @(t,x,u) x(1)-x(3);
xinit = [h1;0;h2;0];
[y,~,~,~,p] = step(sys,t,pFcn,RespConfig('InitialState',xinit));

figure(1), plot(t,y(:,1),t,y(:,2),t,abs(p-a1))
legend('y1','y2','|p-a1|')
title('k2 = 300')

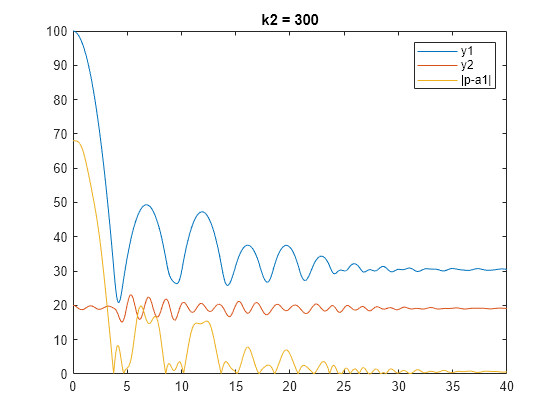
Figure contains an axes object. The axes object with title k2 = 300 contains 3 objects of type line. These objects represent y1, y2, |p-a1|.

曲線は質量の位置を示します。シミュレーションが開始されると、質量 1 は質量 2 に衝突するまで自由落下します。衝突すると質量 2 は押し付けられますが、ただちに跳ね返り、質量 1 を押し戻します。2 つの質量は、 $y_{gap} < a1$ である期間中は接触しています。質量が停止するときの質量の平衡値は、重力による静的な整定により決定されます。

高い床剛性

次に、k2 を 30,000 g/s^2 に設定して、硬い表面に対する応答をシミュレートします。

k2 = 3e4;   % spring constant for second mass (g/s^2)
sys = lpvss("ygap",@(t,p) BouncingBallDF(t,p,k2));

t = 0:0.05:80;
[y,~,~,~,p] = step(sys,t,pFcn,RespConfig('InitialState',xinit));

figure(2), plot(t,y(:,1),t,y(:,2),t,abs(p-a1))
legend('y1','y2','|p-a1|')
title('k2 = 3e4')

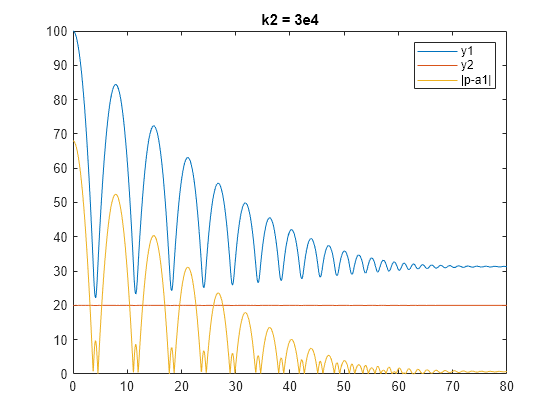
Figure contains an axes object. The axes object with title k2 = 3e4 contains 3 objects of type line. These objects represent y1, y2, |p-a1|.

高い床剛性では、衝突時に質量 2 が押し付けられません。代わりに、より高い位置まで質量 1 を押し戻します。また、質量 1 が整定するまでに跳ね返る回数が多くなります。

データ関数のコード

type BouncingBallDF.m

function [A,B,C,D,E,dx0,x0,u0,y0,Delays] = BouncingBallDF(~,p,k2)
% p = gap y1-y2
m1 = 7;     % first mass (g)
k1 = 100;   % spring constant for first mass (g/s^2)
c1 = 2;     % damping coefficient associated with first mass (g/s)

m2 = 20;    % second mass (g)
%k2 = 300;   % spring constant for second mass (g/s^2)
c2 = 5;     % damping coefficient associated with second mass (g/s)

g = 9.81;   % gravitational acceleration (m/s^2)

a1 = 12;    % uncompressed lengths of spring 1 (mm)
a2 = 20;    % uncompressed lengths of spring 2 (mm)

if p>a1
   % Uncoupled
   A11 = [0 1; 0 0];
   B11 = [0; -g];
   C11 = [1 0];
   D11 = 0;

   A12 = [0 1; -k2/m2, -c2/m2];
   B12 = [0; -g+(k2*a2/m2)];
   C12 = [1 0];
   D12 = 0;

   A = blkdiag(A11, A12);
   B = [B11; B12];
   C = blkdiag(C11, C12);
   D = [D11; D12];
else
   A = [ 0        1,         0,             0; ...
      -k1/m1,   -c1/m1,    k1/m1,         c1/m1;...
      0,        0,         0,             1; ...
      k1/m2,    c1/m2,     -(k1+k2)/m2,   -(c1+c2)/m2];

   B = [0; -g+k1*a1/m1; 0; -g+(k2/m2*a2)-(k1/m2*a1)];
   C = [1 0 0 0; 0 0 1 0];
   D = [0;0];
end
E = [];
dx0 = [];
x0 = [];
u0 = [];
y0 = [];
Delays = [];

参考

lpvss | sample

跳ねるボールの LPV モデル

中程度の床剛性

高い床剛性

データ関数のコード

参考

トピック