sumblk

名前ベースの相互接続のための加算結合

構文

S = sumblk(formula)

S = sumblk(formula,signalsize)

S = sumblk(formula,signames1,...,signamesN)

説明

S = sumblk(formula) は、formula で記述された加算結合を伝達関数 (tf) モデル S の形式で作成します。string の formula は、"e = r - y" のように、S のスカラーの入力信号と出力信号を関連させる方程式を指定します。関数は S の InputName プロパティと OutputName プロパティを formula に基づいて設定します。S と connect を併用して、動的システム モデルを相互に接続し、ブロック線図用の統合モデルを導出します。

S = sumblk(formula,signalsize) はベクトル値の加算結合を返します。入力信号と出力信号は signalsize 個の要素をもつベクトルです。sumblk は、formula の信号名のベクトル拡張によって InputName プロパティと OutputName プロパティを設定します。

S = sumblk(formula,signames1,...,signamesN) は、formula 内のプレースホルダーを信号名 signames で置き換えます。formula で % で始まる信号名を使用してプレースホルダーを示します。signames 引数の数は、formula 内のプレースホルダーの数と一致しなければなりません。formula 内のプレースホルダーが、1 つ目は signames1、2 つ目は signames2 のように順番に置き換えられます。

例

スカラー値の信号をもつ加算結合

以下の図に示す加算結合を作成します。すべての信号はスカラー値。

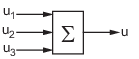
この加算結合には式 u = u1 + u2 + u3 があります。sumblk で次の式を使用して加算結合を作成します。

S = sumblk('u = u1 + u2 + u3');

S は、和 u = u1 + u2 + u3 の伝達関数 (tf) 表現です。つまり、S は 3 つの入力と 1 つの出力をもつ静的ゲインの tf であり、入力の和と等しくなります。伝達関数 S は式からその入力と出力の名前を取得します。

S.OutputName

ans = 1×1 cell array
    {'u'}

S.InputName

ans = 3×1 cell
    {'u1'}
    {'u2'}
    {'u3'}

したがって、S をconnectコマンドの名前ベースの構文で使用して、次のブロック線図のシステムのような統合モデルを作成できます。

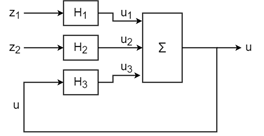
これを行うには、H1、H2、および H3 の LTI モデルを作成し、それらの入力と出力の名前をブロック線図に従って指定します。この例では、伝達関数を使用します。

H1 = tf(1,[1 2],"InputName","z1","OutputName","u1");
H2 = tf([1 -2],[1 1],"InputName","z2","OutputName","u2");
H3 = tf(2,[2 1],"InputName","u","OutputName","u3");

モデルと加算結合を接続して、入力 z1 および z2 と出力 u をもつ統合モデルを作成します。connect コマンドにより、コンポーネントの出力が名前の一致する入力に自動的に接続されます。

T = connect(H1,H2,H3,S,{"z1","z2"},{"u"});
T.InputName

ans = 2×1 cell
    {'z1'}
    {'z2'}

T.OutputName

ans = 1×1 cell array
    {'u'}

ベクトル値の信号をもつ加算結合

加算結合 v = u - d を作成します。ここで、u、d、v は長さ 2 のベクトル値信号です。この加算結合を次のブロック線図に示します。各矢印は 2 つの信号を表しています。

この加算結合は v(1) = u(1) - d(1) および v(2) = u(2) - d(2) を出力します。この結合を sumblk を使用して作成するには、式と信号長の両方を指定します。

S = sumblk('v = u - d',2);
size(S)

Transfer function with 2 outputs and 4 inputs.

結果は 4 つの入力と 2 つの出力をもつ伝達関数になります。d および u のそれぞれ 2 つの入力と v の 2 つの出力です。sumblk は信号名のベクトル拡張を自動的に実行し、それらを S.InputName および S.OutputName に割り当てます。

S.InputName

ans = 4×1 cell
    {'u(1)'}
    {'u(2)'}
    {'d(1)'}
    {'d(2)'}

S.OutputName

ans = 2×1 cell
    {'v(1)'}
    {'v(2)'}

他の MIMO 伝達関数を使用する場合と同じように、S を他の動的システム モデルに接続して統合モデルを作成できます。たとえば、次の 2 チャネルのフィードバック ループを表すモデルを作成するとします。このフィードバック ループで、ブロック線図の各線は 2 つの信号を表しています。

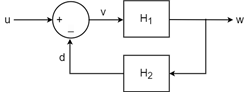
H1 と H2 の 2 入力 2 出力のモデルを作成し、それらの InputName プロパティと OutputName プロパティをブロック線図で示されているように設定します。この例では、ランダムな状態空間モデルを使用します。

H1 = rss(3,2,2);
H1.InputName = 'v';
H1.OutputName = 'w';

H2 = rss(3,2,2);
H2.InputName = 'w';
H2.OutputName = 'd';

sumblk が S の信号名を拡張するのと同じように、動的システム モデルの信号名が自動的に拡張されることに注意してください。たとえば、H1 の出力を確認します。

H1.OutputName 

ans = 2×1 cell
    {'w(1)'}
    {'w(2)'}

この拡張は connect コマンドでも実行されます。したがって、次のコマンドで統合システムを組み立てることができます。

T = connect(S,H1,H2,'u','w');
size(T)

State-space model with 2 outputs, 2 inputs, and 6 states.

ベクトル値の信号をもつ加算結合での個々の名前の指定

ベクトル値の信号をもつ加算結合の例で示しているように、ベクトル信号の加算結合を作成する場合、既定では指定した信号名に sumblk でインデックスが付加されます。このベクトル拡張の代わりに個別の信号名を指定する必要がある場合は、名前を指定する信号を加算結合の式でプレースホルダーを使用して表します。次に、signames 入力引数を使用して、加算結合の作成時にプレースホルダーと置き換える特定の名前を指定します。

たとえば、次の式をもつ加算結合を作成します。

$$\begin{array}{l}e\left(1\right)=setpoint\left(1\right)-alpha\\ e\left(2\right)=setpoint\left(2\right)-q\end{array}$$

この式の加算結合を次のブロック線図に示します。setpoint は 2 つの入力を表し、e は 2 つの出力を表しています。

この加算結合を作成するには、sumblk で e と setpoint を拡張し、signames 引数で指定する特定の信号名に対しては % で始まる信号名をプレースホルダーとして使用します。

formula = 'e = setpoint - %y';
signames = ["alpha","q"];
S = sumblk(formula,signames);

sumblk は、プレースホルダー %y を信号名 alpha および q に置き換え、他の信号名を拡張します。sumblk はベクトル信号のサイズを signames の信号数から取得することに注意してください。したがって、S の入力 setpoint と出力 e のそれぞれに 2 つの信号が含まれます。

S.InputName

ans = 4×1 cell
    {'setpoint(1)'}
    {'setpoint(2)'}
    {'alpha'      }
    {'q'          }

S.OutputName

ans = 2×1 cell
    {'e(1)'}
    {'e(2)'}

この構文は、InputName プロパティまたは OutputName プロパティが既に設定されている既存のモデルを接続するための加算結合を作成する場合に特に便利です。たとえば、次の 2 入力 2 出力の状態空間モデルについて考えてみます。

A = [-0.004 0.03; 0.03 -0.19];
B = [0.3 0.2; -0.06 0];
C = [0.99 0.5; 0 0];
D = 0;
G = ss(A,B,C,D);
G.InputName = {'angle','rate'};
G.OutputName = {'current','temp'};

G の出力を基準入力のペアから抽出する次のような加算結合を作成します。

$$\begin{array}{l}e\left(1\right)=ref\left(1\right)-current\\ e\left(2\right)=ref\left(2\right)-temp\end{array}$$

これを行うには、式でそれらの信号にプレースホルダーを使用します。次に、G.OutputName を signames の入力として使用します。

S = sumblk('e = ref - %outputs',G.OutputName);
S.InputName

ans = 4×1 cell
    {'ref(1)' }
    {'ref(2)' }
    {'current'}
    {'temp'   }

プレースホルダーを複数使用して、式の複数の要素を置き換えることができます。sumblk は指定された順序でプレースホルダーを置き換えます。たとえば、基準信号に ref(1) および ref(2) に代わる特定の名前を付けます。

refnames = ["refcur","reftemp"];
S = sumblk('e = %refs - %outputs',refnames,G.OutputName);
S.InputName

ans = 4×1 cell
    {'refcur' }
    {'reftemp'}
    {'current'}
    {'temp'   }

入力引数

formula — 加算結合の入力信号と出力信号を関連させる方程式

string | 文字ベクトル

加算結合伝達関数 S の入力信号と出力信号を関連させる方程式。string または文字ベクトルとして指定します。たとえば、次のブロック線図の加算結合について考えてみます。

この加算結合を 3 入力 1 出力の伝達関数として表すには、次のコマンドを使用します。

formula = "e = r + d - y";
S = sumblk(formula);

ベクトル値の信号の場合、必要に応じて 1 つ以上のプレースホルダーを formula で使用して、sumblk が S.InputName および S.OutputName に割り当てる名前を制御できます。formula にプレースホルダーを配置するには、% で始まる信号名を使用します。信号名を S に割り当てる際、sumblk コマンドは、各プレースホルダーを signames 引数で指定された名前に置き換えます。

このようなプレースホルダーは、名前の付いた信号をもつ既存のモデルを接続するための加算結合を作成するのに特に便利です。たとえば、C と G が動的システム モデルであり、InputName と OutputName プロパティがそれぞれ空ではない場合は、以下の式を使用して、加算結合を作成できます。

S = sumblk("%e = r - %y",C.InputName,G.OutputName)

sumblk は、%e と %y の代わりに、それぞれ C.InputName と G.OutputName を使用します。C.InputName と G.OutputName のベクトルの次元は一致しなければなりません。sumblk は信号 r に同じ次元を割り当てます。例については、ベクトル値の信号をもつ加算結合での個々の名前の指定を参照してください。

signalsize — 各信号の要素数

1 (既定値) | 正の整数

S の各入力信号と出力信号の要素数。正の整数として指定します。signalsize を 1 より大きく設定すると、ベクトル値の信号で動作する加算結合を指定することができます。たとえば、S = sumblk("e = r - y",2) では、入力 r および y と出力 e のそれぞれが 2 要素のベクトル信号である加算結合が作成されます。ベクトル値の信号をもつ加算結合を参照してください。

signames — プレースホルダーと置き換える信号名

string 配列 | 文字ベクトルの cell 配列

引数 formula 内のプレースホルダー (% で始まる信号名) と置き換える信号名。string 配列または文字ベクトルの cell 配列として指定します。formula 内のプレースホルダーごとに 1 つの signames 引数を指定します。

signames は、以下のように設定します。

• string 配列 (例: ["alpha","q"])。

• 信号名の cell 配列 (例: {'alpha','q'})。

• MATLAB^® ワークスペースのモデルの InputName または OutputName プロパティ。以下に例を示します。

  S = sumblk("%e = r - y",C.InputName)

  このコマンドは、MATLAB ワークスペースのモデル C の入力と同じ名前の出力をもつ加算結合を作成します。signames の使用方法を示す例については、ベクトル値の信号をもつ加算結合での個々の名前の指定を参照してください。

  プレースホルダーと signames 引数を使用する場合、sumblk で S の信号のベクトル長が設定されます。複数のプレースホルダーを使用する場合は、引数 signames のすべてで信号数が同じでなければなりません。

出力引数

S — 加算結合の伝達関数

tf モデル

加算結合の伝達関数。tf モデルとして返されます。

sumblk は S の InputName プロパティと OutputName プロパティを formula 内の信号名を使用して設定します。たとえば、「S = sumblk("e = r + d - y")」と入力すると、sumblk は S.InputName = {'r';'d';'y'} および S.OutputName = {'e'} をもつ S を作成します。S を他の動的システム モデルと相互接続して複合システムを作成するには、これらの入力と出力の名前を使用します。例については、スカラー値の信号をもつ加算結合を参照してください。

signalsize が 1 より大きい場合、S には formula の信号名ごとに signalsize 個の入力 (または出力) が含まれます。関数は、formula で指定された信号名に {'e(1)','e(2)',...} のようなベクトル拡張を適用して S.InputName および S.OutputName を設定します。例については、ベクトル値の信号をもつ加算結合を参照してください。

formula でプレースホルダーを使用する場合、sumblk は S の InputName プロパティと OutputName プロパティを signames で指定された名前を使用して設定します。例については、ベクトル値の信号をもつ加算結合での個々の名前の指定を参照してください。

バージョン履歴

R2008a で導入

参考

connect | series | parallel

トピック

• マルチループ制御システム
• 固定コンポーネントと調整可能なコンポーネントを含む MIMO 制御システム