tpcdec

ターボ積符号 (TPC) 復号化器

構文

decoded = tpcdec(llr,N,K)

decoded = tpcdec(llr,N,K,S)

decoded = tpcdec(llr,N,K,S,maxnumiter)

decoded = tpcdec(llr,N,K,S,maxnumiter,earlyterm)

[decoded,actualnumiter] = tpcdec(___)

説明

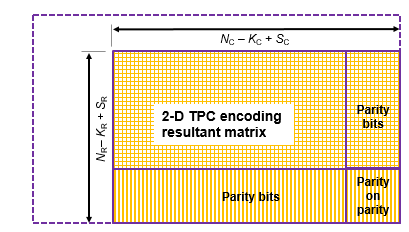
decoded = tpcdec(llr,N,K) は、コードワード長 N とメッセージ長 K により指定される 2 つの線形ブロック符号を使用して、入力対数尤度比 llr で 2 次元 TPC 復号化を実行します。2 次元 TPC 復号化の詳細については、ターボ積符号の復号化を参照してください。

decoded = tpcdec(llr,N,K,S) は、コードワード長 (N–K+S) とメッセージ長 S により指定される 2 次元 TPC 復号化器を使用して、短縮形の llr で 2 次元 TPC 復号化を実行します。

decoded = tpcdec(llr,N,K,S,maxnumiter) は、maxnumiter 回反復する 2 次元 TPC 復号化を実行します。フルレングスのメッセージで maxnumiter を使用するには、S を空 [ ] として指定します。

decoded = tpcdec(llr,N,K,S,maxnumiter,earlyterm) は 2 次元 TPC 復号化を実行し、maxnumiter 復号化反復の前にコンポーネント符号の計算されたシンドロームまたはパリティ チェックがゼロと評価された場合は、早期終了します。フルレングスのメッセージで maxnumiter および earlyterm を使用するには、S を空 [ ] として指定します。

[decoded,actualnumiter] = tpcdec(___) は、上記のいずれかの構文を使用して 2 次元 TPC 復号化を実行した後に、復号化の実際の反復回数も返します。

例

フルレングスの TPC 符号を使用した復号化

16-QAM 復調から近似対数尤度比出力信号を復号化します。

はじめに、拡張されたハミング符号と拡張 BCH 符号で 2 次元ターボ積符号化 (TPC) を使用して、ランダム ビット ベクトルを符号化します。

TPC 符号化で使用する (N,K) 符号ペアを指定します。

N = [32;16]; 
K = [21;11]; 

ランダム メッセージ ビットの列ベクトルを生成し、メッセージを TPC 符号化します。メッセージ ビットを、K の要素の積に等しい長さのベクトルとして指定します。

msg = randi([0 1],prod(K),1);
code = tpcenc(msg,N,K);

16-QAM 変調を適用します。信号に AWGN を追加します。信号を復調して、近似 LLR を出力します。

M = 16;
snr = 10;

txsig = qammod(code,M,'InputType','bit', ...
    'UnitAveragePower',true);

rxsig = awgn(txsig,snr,'measured');

llr = qamdemod(rxsig,M,'OutputType','approxllr', ...
    'UnitAveragePower',true,'NoiseVariance',10.^(-snr/10));

3 回の反復を使用する TPC 復号化を実行します。復調器の出力は負のバイポーラ マッピングされていて、TPC 復号化器は正のバイポーラ マッピングされた入力を予期しているため、復調した信号出力は復号化器入力時に反転されなければなりません。復号化した信号のビット誤り数をチェックします。

iterations = 3;
decoded = tpcdec(-llr,N,K,[],iterations);

numerr = biterr(msg,decoded)

numerr = 0

短縮形の TPC 符号を使用した復号化

短縮形の TPC 符号を復号化します。QPSK 変調を適用し、QPSK 復調から得られた近似対数尤度比信号を出力します。

はじめに、拡張されたハミング符号と拡張 BCH 符号で 2 次元ターボ積符号化 (TPC) を使用して、ランダム ビット ベクトルを符号化します。

TPC 符号化用の (N,K) 符号ペアと S を指定します。

N = [32;32];
K = [21;26];
S = [19;24];

ランダム メッセージ ビットの列ベクトルを生成し、メッセージを TPC 符号化します。短縮メッセージ ビットを、S の要素の積に等しい長さのベクトルとして指定します。

msg = randi([0 1],prod(S),1);
code = tpcenc(msg,N,K,S);

QPSK 変調を適用します。信号に AWGN を追加します。信号を復調して、近似 LLR を出力します。

M = 4;
snr = 3;

txsig = qammod(code,M,'InputType','bit', ...
    'UnitAveragePower',true);

rxsig = awgn(txsig,snr,'measured');

llr = qamdemod(rxsig,M,'OutputType','approxllr', ...
    'UnitAveragePower',true,'NoiseVariance',10.^(-snr/10));

2 回の反復を使用する TPC 復号化を実行します。復調器の出力は負のバイポーラ マッピングされていて、TPC 復号化器は正のバイポーラ マッピングされた入力を予期しているため、復調した信号出力は復号化器入力時に反転されなければなりません。復号化した信号のビット エラー レートをチェックします。

iterations = 2;
decoded = tpcdec(-llr,N,K,S,iterations);

[~,ber] = biterr(msg,decoded)

ber = 0

短縮と早期終了を使用した TPC 復号化

短縮形の TPC 符号を復号化し、復号化の早期終了を指定します。QPSK 変調を適用し、QPSK 復調から得られた近似対数尤度比信号を出力します。

はじめに、拡張されたハミング符号と拡張 BCH 符号で 2 次元ターボ積符号化 (TPC) を使用して、ランダム ビット ベクトルを符号化します。TPC 符号化用の (N,K) 符号ペアと S を指定し、最大 10 回の復号化反復を指定します。信号に対して QPSK 変調を実行します。

n = [64; 32];
k = [51; 26];
s = [49; 24];
maxnumiter = 10;
M = 4;

msg = randi([0 1],prod(s),1);  % Random bits
code = tpcenc(msg,n,k,s);

txsig = qammod(code,M,'InputType','bit', ...
    'UnitAveragePower',true);

送信信号にノイズを付加します。

snr = 5;
rxsig = awgn(txsig,snr,'measured');

近似 LLR デマッピングを使用して、受信信号を復調します。

llr = qamdemod(rxsig,M,'OutputType', ...
    'approxllr','UnitAveragePower',true, ...
    'NoiseVariance',10.^(-snr/10));

TPC 復号化の最大反復回数を指定し、実行された実際の反復回数を返します。TPC 復号化の早期終了は既定でオンになっています。誤り数と実行された反復回数を表示します。

[decoded,actualNumIter] = tpcdec(-llr,n,k,s,maxnumiter);
numErr = biterr(msg,decoded);
disp(['Terminated after ' num2str(actualNumIter) ' iterations.' ...
    ' Number of errors = ' num2str(numErr) '.']);

Terminated after 4 iterations. Number of errors = 0.

入力引数

llr — 対数尤度比

列ベクトル

対数尤度比。列ベクトルとして指定します。

• フルレングスの符号では、入力列ベクトルの長さは、N の要素の積です。

• 短縮符号では、入力列ベクトルの長さは、(N–K+S) の要素の積です。

データ型: double | single

N — コードワード長

2 要素の整数ベクトル

コードワード長。2 要素の整数ベクトル [N_R; N_C] として指定します。N_R は、積符号行列の行数を表します。N_C は、積符号行列の列数を表します。N_R および N_C の詳細については、ターボ積符号の復号化を参照してください。有効な (N(i),K(i)) 符号ペアの一覧については、詳細を参照してください。

データ型: double

K — メッセージ長

2 要素の整数ベクトル

メッセージ長。2 要素の整数ベクトル [K_R; K_C] として指定します。フルレングスのメッセージの場合、入力 LLR を含む入力列ベクトルは、K_R 行 K_C 列の行列に調整されます。K_R は、メッセージ行列の行数を表します。K_C は、メッセージ行列の列数を表します。K_R および K_C の詳細については、ターボ積符号の復号化を参照してください。有効な (N(i),K(i)) 符号ペアの一覧については、詳細を参照してください。

データ型: double

S — 短縮メッセージ長

2 要素の整数ベクトル

短縮メッセージ長。2 要素の整数ベクトル [S_R; S_C] として指定します。短縮メッセージの場合、入力 LLR を含む入力列ベクトルは、S_R 行 S_C 列の行列に調整されます。S_R は、行列の行数を表します。S_C は、行列の列数を表します。S_R および S_C の詳細については、ターボ積符号の復号化を参照してください。

このパラメーターを指定する場合は、(N(i) – K(i) + S(i), S(i)) 符号に短縮されたフルレングスの TPC 符号の N ベクトルと K ベクトルを指定します。

データ型: double

maxnumiter — 復号化反復の最大数

4 (既定値) | 正の整数

復号化の最大反復回数。正の整数を指定します。

データ型: double

earlyterm — 早期終了の有効化

true (既定値) | false

復号化の早期終了を有効にします。logical として指定します。earlyterm を true にすると、maxnumiter 復号化反復の前にコンポーネント符号の計算されたシンドロームまたはパリティ チェックがゼロと評価された場合は、復号化が早期終了します。

データ型: double

出力引数

decoded — TPC 復号化されたメッセージ

列ベクトル

TPC 復号化されたメッセージ。列ベクトルとして返されます。

• フルレングスの符号では、返される列ベクトルの長さは、K の要素の積です。

• 短縮符号では、返される列ベクトルの長さは、S の要素の積です。

データ型: logical

actualnumiter — 復号化の実際の反復回数

正の整数

実行された復号化の実際の反復回数。正の整数として返されます。

データ型: double

詳細

コンポーネント符号

次の表に、行 (N_R,K_R) パラメーターおよび列 (N_C,K_C) パラメーターの、サポートされているコンポーネント符号のペアを示します。

• N_R と K_R は、それぞれ積符号行列とメッセージ行列の行数を表します。

• N_C と K_C は、それぞれ積符号行列とメッセージ行列の列数を表します。

各符号タイプ内で、任意の 2 つのコンポーネント符号のペアで 2 次元 TPC 符号を作成できます。この表には、各符号ペアの誤り訂正能力も含まれています。

コード タイプ	コンポーネント符号ペア (NR,KR) および (NC,KC)	誤り訂正能力 (T)
ハミング符号	(255,247)	1
	(127,120)	1
	(63,57)	1
	(31,26)	1
	(15,11)	1
	(7,4)	1
拡張ハミング符号	(256,247)	1
	(128,120)	1
	(64,57)	1
	(32,26)	1
	(16,11)	1
	(8,4)	1
BCH 符号	(255,239)	2
	(127,113)	2
	(63,51)	2
	(31,21)	2
	(15,7)	2
拡張 BCH 符号	(256,239)	2
	(128,113)	2
	(64,51)	2
	(32,21)	2
	(16,7)	2
パリティ チェック コード	(256,255)	-
	(128,127)	-
	(64,63)	-
	(32,31)	-
	(16,15)	-
	(8,7)	-
	(4,3)	-

ターボ積符号の復号化

ターボ積符号 (TPC) は、前方誤り訂正 (FEC) コードとして使用される連結コードの形式です。組織線形ブロック符号などの 2 つ以上のコンポーネント ブロック コードは、TPC を構築するために使用されます。TPC 復号化器は、反復軟入力、軟出力復号化を実行する Chase 復号化と Pyndiah アルゴリズムを使用して積符号のほぼ最適な復号化を実現します。詳細については、[1]および[2]を参照してください。この復号化器は、2 つの線形ブロック符号を使用して、[2]で説明されている反復軟入力、軟出力 2 次元積符号の復号化を実装します。復号化器は、入力信号として、デジタル復調から得られた軟ビット対数尤度比 (LLR) を予期しています。

メモ

TPC 復号化器は、正のバイポーラ マッピングされた入力、具体的には 0 にマッピングされた –1 と 1 にマッピングされた +1 を予期しています。Communications Toolbox™ の復調器からの出力は、負のバイポーラ マッピング、具体的には 0 にマッピングされた +1 と +1 にマッピングされた –1 です。そのため、復調器からの LLR 出力は、TPC 復号化器によって予期されている正のバイポーラ マッピングされた入力を提供するために、反転されなければなりません。

TPC 復号化器は、フルレングスの符号または短縮符号を復号化します。

 フルレングスのメッセージの TPC 復号化

TPC 符号化されたフルレングスの入力メッセージは、指定された 2 次元 TPC 符号ペアを使用して復号化されます。行方向の復号化では (N_C, K_C) 符号ペアを使用し、列方向の復号化では (N_R, K_R) 符号ペアを使用します。入力ベクトル長は、N_R × N_C でなければなりません。2 次元 TPC 復号化を実行するために、メッセージとパリティ ビットで構成される入力 LLR の列ベクトルは、N_R 行 N_C 列の行列に調整されます。

TPC 復号化器は、反復軟入力、軟出力復号化を実行する Chase 復号化と Pyndiah アルゴリズムを使用して積符号のほぼ最適な復号化を実現します。Chase 復号化では、各列または各行で可能な一連のコードワードを作成します。Pyndiah アルゴリズムでは、次の復号化ステップで必要な軟情報を計算します。

反復軟入力、軟出力復号化

反復軟入力、軟出力復号化は、ブロック線図に示すように、反復ごとに 2 つの復号化ステップを実行します。

復号化の軟入力は、R(m) = R + α(m)W(m) です。

• 反復のループ カウンター i は、i = 1 から指定された反復数までインクリメントします。

• m = 2i – 1 は、復号化ステップのインデックスです。

• R は、受信 LLR 行列です。

• R(m) は、m 番目の復号化ステップの軟入力です。

• W(m) は、m 番目の復号化ステップの入力外部情報です。

• α(m) = [0,0.2,0.3,0.5,0.7,0.9,1,1, ...] で、α は復号化ステップのインデックスに基づいて適用される重み付けの係数です。高次の復号化ステップでは、α = 1 です。

• β(m) = [0.2,0.4,0.6,0.8,1,1, ...] で、β は復号化ステップのインデックスに基づいて適用される信頼性の係数です。高次の復号化ステップでは、β = 1 です。

• D は復号化されたメッセージ ビットを含みます。–1 を 0 に、+1 を 1 にマッピングしてからメッセージ ブロックを列ベクトルに形状変更することで、出力メッセージ ビットが D から求められます。

出力メッセージ ビットは、指定された反復回数が反復された後に求められるか、早期終了が有効になっている場合は符号の収束後に求められます。

TPC 復号化の早期終了

早期終了が有効になっている場合は、行方向および列方向の各復号化ステップで、軟入力の硬判定に対して符号の収束チェックが実行されます。早期終了は、行方向復号化または列方向復号化が収束した後にトリガーされる可能性があります。

すべての行またはすべての列で次の場合に、符号が収束します。

• シンドロームが、符号 (ハミング符号、拡張ハミング符号、BCH 符号、または拡張 BCH 符号) でゼロと評価される。

• パリティ チェックが、パリティ チェック コードでゼロと評価される。

報告される反復回数は、現在進行中の反復の値として評価されます。たとえば、3 回目の反復での行方向復号化の後に (2.5 回目の復号化ステップの後に) 符号の収束チェックが満たされた場合、返される反復回数は 3 になります。

 短縮メッセージの TPC 復号化

TPC 符号化された短縮形の入力メッセージは、指定された 2 次元 TPC 符号ペアを使用して復号化されます。行方向の復号化では (N_C – K_C + S_C, S_C) 符号ペアを使用し、列方向の復号化では (N_R – K_R + S_R, S_R) 符号ペアを使用します。入力ベクトル長は、(N_R – K_R + S_R) × (N_C– K_C + S_C) でなければなりません。短縮メッセージの 2 次元 TPC 復号化を実行するために、短縮メッセージとパリティ ビットで構成される入力 LLR の列ベクトルは、(N_R – K_R + S_R) 行 (N_C – K_C + S_C) 列の行列に調整されます。

TPC 復号化器は、受信した短縮メッセージ LLR をフル レングスのコードと同様に処理しますが、次が異なります。

• 短縮形の受信コードワード内のビット位置は、-1 に設定されます。

• Chase アルゴリズムは、最も信頼性の低いビットを選択している間、短縮形のビット位置を考慮しません。

参照

[1] Chase, D. "Class of Algorithms for Decoding Block Codes with Channel Measurement Information." IEEE Transactions on Information Theory, Volume 18, Number 1, January 1972, pp. 170–182.

[2] Pyndiah, R. M. "Near-Optimum Decoding of Product Codes: Block Turbo Codes." IEEE Transactions on Communications. Volume 46, Number 8, August 1998, pp. 1003–1010.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• TPC パラメーター N、K および S は定数値でなければなりません。これらの各パラメーターで使用される値が変化しない場合、式または変数で代入することができます。

バージョン履歴

R2018a で導入

参考

関数

• bchdec | tpcenc

オブジェクト

• comm.BCHDecoder

ブロック

• TPC Decoder