ウェーブレットパケット

ウェーブレットパケットの手法はウェーブレット分解の一般化であり、より豊かな信号解析を提供します。

ウェーブレットパケットの原子は、位置、(ウェーブレット分解と同様の) スケール、周波数の 3 つの自然に解釈されるパラメーターでインデックス付けされた波形です。

任意の直交ウェーブレット関数に対し、"ウェーブレットパケット基底" と呼ばれる基底のライブラリを生成します。これらの基底はそれぞれ、信号を符号化し、グローバルエネルギーを保存し、正確な特徴を再構成する特定の方法を提供します。ウェーブレットパケットを使用して、与えられた信号をさまざまに展開できます。その後、エントロピーベースの基準で、与えられた信号の最適な分解を選択します。

ウェーブレットパケット分解と最適な分解の選択の両方にシンプルで効率的なアルゴリズムが存在します。さらに、最適な信号符号化およびデータ圧縮での直接の応用で、適応フィルター処理アルゴリズムを生成できます。

ウェーブレットからウェーブレットパケットへ

直交ウェーブレット分解の処理において、一般的な手順では Approximation 係数を 2 つの部分に分割します。分割後、Approximation 係数から成るベクトルと Detail 係数から成るベクトルが、ともに粗いスケールで得られます。連続する 2 つの Approximation の間で失われた情報は、Detail 係数に取得されています。さらに、次の手順は新しい Approximation 係数ベクトルの分割で構成されます。一連の Detail が再解析されることはありません。

ウェーブレットパケットにおいても同様に、Approximation ベクトルの分割と同じ方法を使用して、各 Detail 係数ベクトルも 2 つの部分に分解されます。これにより、極めて豊かな解析が提供されます。次の図に示すような完全二分木が生成されます。

レベル 3 でのウェーブレットパケット分解ツリー

この分解の考え方は、スケール指向の分解から始めて、得られた信号を周波数サブバンドで解析することです。

実際のウェーブレットパケット: はじめに

この例では次を使用します。

ライブスクリプトを開く

この例では、ウェーブレット解析とウェーブレットパケット解析の違いを示します。

ウェーブレットパケットスペクトル

フーリエ変換を使用する広義定常信号のスペクトル解析は、十分に確立されています。非定常信号については、短時間フーリエ変換 (STFT) などの局所フーリエ手法が存在します。概要については、短時間フーリエ変換を参照してください。

ウェーブレットは時間および周波数で局在化するので、STFT に相当するウェーブレットベースのものを非定常信号の時間-周波数解析に使用することができます。たとえば、連続ウェーブレット変換 (CWT) に基づいたスカログラムを構築できます。しかし、CWT を使用する潜在的な欠点は、計算に時間がかかることです。

離散ウェーブレット変換 (DWT) は入力信号の時間-周波数分解ができますが、DWT での周波数分解能の度合いは、一般に実用的な時間-周波数解析には粗すぎると考えられています。

DWT ベースの手法と CWT ベースの手法の間の折衷案として、ウェーブレットパケットは、計算効率が高く、十分な周波数分解能がある代替手法を提供します。wpspectrumを使用して、ウェーブレットパケットを使用した信号の時間-周波数解析を実行できます。

ウェーブレットパケットを使用した局所スペクトル解析

以下の例では、ウェーブレットパケットを使用して局所スペクトル解析を実行する方法について説明します。stft (Signal Processing Toolbox)をベンチマークとして使用し、ウェーブレットパケットのスペクトルと比較します。

正弦波

周波数 128 Hz の正弦波を生成します。信号を 1 kHz でサンプリングします。

Fs = 1e3;
frq = 128;
t = 0:1/Fs:2;
sig = sin(2*pi*frq*t);

関数wpdecを使用して、信号のウェーブレットパケット分解をレベル 6 まで求めます。sym8 ウェーブレットを使用します。ウェーブレットパケットのパワースペクトルの大きさをプロットします。

figure
level = 6;
wpt = wpdec(sig,level,"sym8");
[spec,tm,frq] = wpspectrum(wpt,Fs,"plot");

Figure contains an axes object. The axes object with title Wavelet packet decomposition, xlabel Time (secs), ylabel Freq (Hz) contains 66 objects of type image, text.

同じ信号の STFT の大きさのプロットと比較します。

windowsize = 128;
window = hanning(windowsize);
noverlap = windowsize-1;
stft(sig,Fs,Window=window,OverlapLength=noverlap, ...
    FrequencyRange="onesided")
colorbar off
colormap("default")

Figure contains an axes object. The axes object with title Short-Time Fourier Transform, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

正弦波の和

周波数がそれぞれ 64 Hz と 128 Hz の 2 つの正弦波の和を生成します。信号を 1 kHz でサンプリングします。

Fs = 1e3;
frq1 = 64;
frq2 = 128;
t = 0:1/Fs:2;
sig = sin(2*pi*frq1*t) + ...
    sin(2*pi*frq2*t);

ウェーブレットパケットのパワースペクトルの大きさをプロットします。

clf
wpt = wpdec(sig,level,"sym8");
[Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");

Figure contains an axes object. The axes object with title Wavelet packet decomposition, xlabel Time (secs), ylabel Freq (Hz) contains 66 objects of type image, text.

STFT の大きさのプロットと比較します。

stft(sig,Fs,Window=window,OverlapLength=noverlap, ...
    FrequencyRange="onesided")
colorbar off
colormap("default")

Figure contains an axes object. The axes object with title Short-Time Fourier Transform, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

急激な周波数の変化

2 秒間に 16 Hz から 64 Hz まで周波数が急激に変化する信号を生成します。信号を 500 Hz でサンプリングします。

Fs = 500;
frq1 = 16;
frq2 = 64;
t = 0:1/Fs:4;
sig = sin(2*pi*frq1*t).*(t<2) + ...
    sin(2*pi*frq2*t).*(t>=2);

ウェーブレットパケットのパワースペクトルの大きさをプロットします。

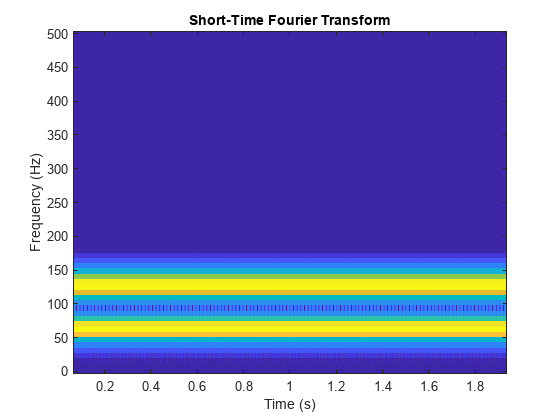
clf
wpt = wpdec(sig,level,"sym8");
[Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");

Figure contains an axes object. The axes object with title Wavelet packet decomposition, xlabel Time (secs), ylabel Freq (Hz) contains 66 objects of type image, text.

STFT の大きさのプロットと比較します。

stft(sig,Fs,Window=window,OverlapLength=noverlap, ...
    FrequencyRange="onesided")
colorbar off
colormap("default")

Figure contains an axes object. The axes object with title Short-Time Fourier Transform, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

線形チャープ

1 kHz でサンプリングされた線形チャープを生成します。

Fs = 1e3;
frq = 128;
t = 0:1/Fs:2;
sig = sin(2*pi*frq*t.^2);

ウェーブレットパケットのパワースペクトルの大きさをプロットします。

clf
wpt = wpdec(sig,level,"sym8");
[Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");

Figure contains an axes object. The axes object with title Wavelet packet decomposition, xlabel Time (secs), ylabel Freq (Hz) contains 66 objects of type image, text.

STFT の大きさのプロットと比較します。

stft(sig,Fs,Window=window,OverlapLength=noverlap, ...
    FrequencyRange="onesided")
colorbar off
colormap("default")

Figure contains an axes object. The axes object with title Short-Time Fourier Transform, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

2 次チャープ

2 次チャープを生成します。

sig = wnoise("quadchirp",10);
len = length(sig);
t = linspace(0,5,len);
Fs = 1/t(2);

ウェーブレットパケットのパワースペクトルの大きさをプロットします。

clf
wpt = wpdec(sig,level,"sym8");
[Spec,Time,Freq] = wpspectrum(wpt,Fs,"plot");

Figure contains an axes object. The axes object with title Wavelet packet decomposition, xlabel Time (secs), ylabel Freq (Hz) contains 66 objects of type image, text.

STFT の大きさのプロットと比較します。

stft(sig,Fs,Window=window,OverlapLength=noverlap, ...
    FrequencyRange="onesided")
colorbar off
colormap("default")

Figure contains an axes object. The axes object with title Short-Time Fourier Transform, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

ウェーブレットパケットの作成

ライブスクリプトを開く

ウェーブレットパケット生成の計算手法は、直交ウェーブレットを使用すると簡単です。まず、ウェーブレットに対応する長さ $2 N$ の 2 つのフィルター $h (n)$ と $g (n)$ から始めます。

帰納法により、関数列 ${W_{n} (x), n = 0, 1, 2, \dots}$ を次のように定義します。

$W_{2 n} (x) = \sqrt{2} \sum_{k = 0}^{2 N - 1} h (k) W_{n} (2 x - k)$

$W_{2 n + 1} (x) = \sqrt{2} \sum_{k = 0}^{2 N - 1} g (k) W_{n} (2 x - k),$

ここで、 $W_{0} (x) = ϕ (x)$ はスケーリング関数、 $W_{1} (x) = ψ (x)$ はウェーブレット関数です。

たとえば、Haar ウェーブレットの場合、次が成り立ちます。

$N = 1, h (0) = h (1) = \frac{1}{\sqrt{2}}$

と

$g (0) = - g (1) = \frac{1}{\sqrt{2}} .$

方程式は次のようになります。

$W_{2 n} (x) = W_{n} (2 x) + W_{n} (2 x - 1)$

と

$W_{2 n + 1} (x) = W_{n} (2 x) - W_{n} (2 x - 1) .$

$W_{0} (x) = ϕ (x)$ は Haar スケーリング関数、 $W_{1} (x) = ψ (x)$ は Haar ウェーブレットです。どちらの関数も閉区間 [-1,1] でサポートされます。次に、 $W_{2 n}$ は、異なるサポート [0,1/2] および [1/2,1] をもつ $W_{n}$ のハーフスケールバージョンを加算することで得られます。

関数 wpfun を使用して、Haar ウェーブレットに関連付けられた $W$ 関数を 1/2^5 グリッド上にプロットします。

[wfun,xgrid] = wpfun("db1",7,5);
t = tiledlayout(2,4);
for k=0:7
    nexttile
    plot(xgrid,wfun(k+1,:),LineWidth=2)
    title("W"+num2str(k))
    ylim([-2 2])
end
title(t,"Haar Wavelet Packets")

元のウェーブレットとして、より正則なウェーブレットから始めて、同様の作成方法を使用すると、このような W 関数系の、より滑らかなバージョンが得られます。すべて、区間 [0, 2N–1] にサポートを持ちます。

関数 wpfun を使用して、db2 ウェーブレットに関連付けられた $W$ 関数をプロットします。

[wfun,xgrid] = wpfun("db2",7,5);
t = tiledlayout(2,4);
for k=0:7
    nexttile
    plot(xgrid,wfun(k+1,:),LineWidth=2)
    title("W"+num2str(k))
    ylim([-3 3])
end
title(t,"db2 Wavelet Packets")

ウェーブレットパケットの原子

関数 ${W_{n} (x), n \in ℕ}$ から始めて、直交ウェーブレットを導くのと同じ方針に従い、3 つのインデックスの付いた解析関数のファミリ (波形) を検討します。

$W_{j, n, k} (x) = 2^{- j / 2} W_{n} (2^{- j} x - k)$

ここで、 $n \in ℕ$ および $(j, k) \in ℤ^{2}$ です。

ウェーブレットのフレームワークと同様に、k は時間の局所化パラメーターで、j はスケールパラメーターと解釈できます。では、n の解釈は何でしょうか。

ウェーブレットパケットの基本的な考え方は、j および k の固定値に対して、W_j,n,k はおおよそ 2^j· k の位置における信号の変動を、スケール 2^j で、最後のパラメーター n の許容される異なる値に対するさまざまな周波数で解析するというものです。

実際、Haar ウェーブレットパケットおよび db2 ウェーブレットパケットに示されたウェーブレットパケットを注意深く確認すると、自然な順序の W_n (n = 0, 1, ..., 7) は、振動数で定義される順序とは厳密には一致しません。正確に言うと、db1 ウェーブレットパケットのゼロクロッシング (アップクロッシングとダウンクロッシング) の回数を数えると、次のようになります。

自然順 n	0	1	2	3	4	5	6	7
db1 W_n のゼロクロッシングの回数	2	3	5	4	9	8	6	7

そのため、主な周波数がその順序により単調に増加するという性質を取り戻すため、自然順から再帰的に取得した "周波数順" を定義すると便利です。

自然順 n	0	1	2	3	4	5	6	7
周波数順 r(n)	0	1	3	2	6	7	5	4

前の図からわかるように、W_r₍_n₎(x) は、おおよそ n 回 "振動" します。

信号 (たとえば、線形チャープ) を解析するには、ウェーブレットパケット係数を自然順ではなく周波数順にしたがって、低い周波数 (一番下) から高い周波数 (一番上) へとプロットするのが適切です。

ウェーブレットパケットツリーに係数をプロットするには、関数 wpviewcf を使用します。

ウェーブレットパケットの構成

関数の集合 $W_{j, n} = {W_{j, n, k} (x), k \in ℤ}$ は、"(j,n) ウェーブレットパケット" です。正の値の整数 j および n に対して、ウェーブレットパケットはツリー状に構成されます。図ツリー状に構成されたウェーブレットパケット (スケール j は深さを定義し、周波数 n はツリー内の位置を定義)のツリーは、最大レベルが 3 に等しい分解となるよう作成されています。各スケール j に対して、パラメーター n の取りうる値は 0、1、...、2^j–1 です。

ツリー状に構成されたウェーブレットパケット (スケール j は深さを定義し、周波数 n はツリー内の位置を定義)

W_j,n (j はスケールパラメーター、n は周波数パラメーター) という表記は、通常のツリーの深さ-位置のラベル付けと一致しています。

ここで、 $W_{0, 0} = {ϕ (x - k), k \in ℤ}$ 、 $W_{1, 1} = {ψ (\frac{x}{2} - k), k \in ℤ}$ です。

ウェーブレットパケット基底のライブラリには、ウェーブレット基底と他の基底がいくつか含まれていることがわかります。そのような基底をいくつか見てみましょう。正確に説明するため、解析対象の信号が存在する (ファミリ W_0,0 が張る) 空間を V₀ とします。その場合、{W_d_,1; d ≥ 1} は V₀ の直交基底です。

厳密に正である各整数 D に対して、{W_D,0, {W_d,1; 1 ≤ d ≤ D}} は V₀ の直交基底です。

また、関数のファミリ {(W_j_+1,2_n), (W_j_+1,2_n₊₁)} は、W_j,n が張る空間の直交基底であることもわかります。これは 2 つの部分空間に分割されます。W_j_+1,2_n が第 1 の部分空間を張り、W_j_+1,2_n₊₁ が第 2 の部分空間を張ります。

この最後の性質によって、ウェーブレットパケットの構成ツリーにおける分割を正確に解釈できます。作成されるノードはすべて、図ウェーブレットパケットツリー: 分割と結合に示す形式だからです。

ウェーブレットパケットツリー: 分割と結合

したがって、ツリー全体のうち、結合されている各二分部分木の葉が、最初の空間の直交基底に相当します。

V₀ に属する有限エネルギーの信号に対して、任意のウェーブレットパケット基底が、正確な再構成を提供します。また、周波数スケールのサブバンドでの情報割り当てを使用して、信号を符号化する固有の方法を提供します。

最適な分解の選択

ライブスクリプトを開く

ウェーブレットパケットライブラリの構成に基づき、与えられた直交ウェーブレットから生じる分解の数を数えるのは自然なことです。

長さ $N = 2^{L}$ の信号は、 $α$ 通りの方法で拡張できます。ここで、 $α$ は、深さ L の完全二分木の二分木部分木の数です。結果として、 $α \geq 2^{N / 2}$ になります ([1]を参照)。

この数値は非常に大きい場合があり、また明示的な列挙は一般に取り扱いが困難であるため、効率的なアルゴリズムで計算できる便利な基準を使って最適な分解を見つけるというのは興味深いことです。最小限の基準については探求を続けています。

加法的性質を満たす関数は、二分木構造の効率的な検索と基本的な分割に適しています。古典的なエントロピーベースの基準はこれらの条件に適合し、与えられた信号の正確な表現について情報関連の性質を表します。エントロピーは、さまざまな分野に共通の概念であり、主に信号処理で使われます。ここでは 4 種類のエントロピー基準を紹介します ([2]を参照)。これ以外にも多くのものが利用でき、簡単に統合できます (wpdecを参照)。以下の式で、s は信号、(si) は正規直交基底での s の係数です。

エントロピー $E$ は、 $E (0) = 0$ と $E (s) = \sum_{i} E (s_{i})$ を満たす加法的コスト関数でなければなりません。

(非正規化) Shannon エントロピーは $E1 (s_{i}) = - s_{i}^{2} \log (s_{i}^{2})$ であるため $E1 (s) = - \sum_{i} s_{i}^{2} \log (s_{i}^{2})$ となる。ただし $0 \log (0) = 0$ 。
$1 \leq p$ の $l^{p}$ ノルムでの集中度は $E2 (s_{i}) = {| s_{i} |}^{p}$ であるため $E2 (s) = \sum_{i} {| s_{i} |}^{p} = {‖ s ‖}_{p}^{p}$ となる。
"エネルギー" の対数エントロピーは $E3 (s_{i}) = \log (s_{i}^{2})$ であるため $E3 (s) = \sum_{i} \log (s_{i}^{2})$ となる。ただし $\log (0) = 0$ 。
エントロピーのしきい値は、 $| s_{i} | > p$ の場合に $E4 (s_{i}) = 1$ であり、それ以外の場合は $0$ であるため、 $E4 (s) = # {i such that | s_{i} | > p}$ は信号がしきい値 $p$ より大きい時点の数となる。

さまざまなエントロピーの計算

エネルギーが 1 に等しい信号を生成します。

s = ones(1,16)*0.25;

s の Shannon エントロピーを計算します。

e1 = -sum((s.^2).*log(s.^2))

e1 = 2.7726

s の $l^{1.5}$ エントロピーを計算します。

e2 = norm(s,1.5)^1.5

e2 = 2.0000

s の "対数エネルギー" エントロピーを計算します。

e3 = sum(log(s.^2))

e3 = -44.3614

しきい値 0.24 を使用して、s のしきい値エントロピーを計算します。

e4 = sum(abs(s)>0.24)

e4 = 16

最小エントロピー分解

この簡単な例では、エントロピーを使用して、新しい分割が最小エントロピー分解を取得する上で関心の対象となるかどうかを判断する方法について説明します。

便宜上、最初に、厳密に非ゼロの値をもつ信号の Shannon エントロピーを計算する無名関数を定義します。

shannon = @(x)(-sum((x.^2).*log(x.^2)));

定数信号を作成します。

w00 = ones(1,16)*0.25;

信号の Shannon エントロピーを計算します。

e00 = shannon(w00)

e00 = 2.7726

関数 dwt を使用し、Haar ウェーブレットを使用して w00 を分割します。

[w10,w11] = dwt(w00,"db1");

レベル 1 での Approximation のエントロピーを計算します。

e10 = shannon(w10)

e10 = 2.0794

元の信号は定数であるため、レベル 1 の Detail は 0 です。したがって、エントロピーは 0 になります。加法的性質のため、分解のエントロピーは e10 + e11 = 2.0794 で与えられます。合計を初期エントロピー e00 = 2.7726 と比較します。e10 + e11 < e00 となるので、分割によってエントロピーが減少します。

Approximation w10 を分割します。

[w20,w21] = dwt(w10,"db1");

w20=0.5*ones(1,4) となり、w21 は 0 です。レベル 2 での Approximation のエントロピーを計算します。

e20 = shannon(w20)

e20 = 1.3863

e20 + 0 < e10 となりました。やはり、分割によってエントロピーは減少します。

分割をさらに 2 回繰り返します。

[w30,w31] = dwt(w20,"db1");
e30 = shannon(w30)

e30 = 0.6931

[w40,w41] = dwt(w30,"db1")

w40 = 1.0000

w41 = 0

e40 = shannon(w40)

e40 = -4.4409e-16

最後の分割処理において、1 つの情報のみが元の信号の再構成に必要であることがわかります。レベル 4 のウェーブレット基底は、Shannon エントロピーによると (e40 + e41 + e31 + e21 + e11 = 0 なのでエントロピーが最適な 0 となる) 最も良い基底です。

関数 wpdec を使用して、元の信号のウェーブレットパケット分解を計算します。

t = wpdec(w00,4,"haar","shannon");

ウェーブレットパケットツリー t は、4 つのレベルをもつ二分木です。元のエントロピー値でラベル付けされたノードをもつ二分木をプロットします。補助関数 helperPlotTreeWithLabels を使用します。補助関数のソースコードは、この例のファイルと同じディレクトリにあります。

helperPlotTreeWithLabels([e00,e10,e20,e30])

Figure contains an axes object. The axes object with xlabel height = 4 contains 6 objects of type line, text. One or more of the lines displays its values using only markers

ベストツリーを計算します。ベストツリーをプロットします。この場合、ベストツリーはウェーブレットツリーに相当します。

bt = besttree(t);
plot(bt)

Figure contains 2 axes objects and other objects of type uimenu. Axes object 1 with title Tree Decomposition contains 17 objects of type line, text. Axes object 2 with title data for node: 0 or (0,0). contains an object of type line.

興味深い部分木

ウェーブレットパケットを使用するには、ツリーに関連する操作とラベル付けが必要です。ユーザーインターフェイスの実装は、これを考慮して構築されています。技術的な詳細については、リファレンスページを参照してください。

レベル D で作成されたウェーブレットパケット分解ツリーに対応する深さ D の完全二分木は、WPT で示されます。

興味深い部分木として次のものがあります。

分解ツリー	葉の集合が基底となる部分木
ウェーブレットパケット分解ツリー	完全二分木: 深さ D の WPT
ウェーブレットパケット最適分解ツリー	WPT の二分部分木
ウェーブレットパケットベストレベルツリー	WPT の完全二分部分木
ウェーブレット分解ツリー	深さ D の WPT の左片側二分部分木
ウェーブレットベスト基底ツリー	WPT の左片側二分部分木

エントロピー基準 E に関して最適な分解の定義を以下のように導出しています。

分解	最適な分解	ベストレベル分解
ウェーブレットパケット分解	2^D 個のツリーから検索	D 個のツリーから検索
ウェーブレット分解	D 個のツリーから検索	D 個のツリーから検索

終端以外のノードについて、次の基本手順を使用して、与えられたエントロピー基準 E に関して最適な部分木を見つけます (ここで、Eopt は最適なエントロピー値を示します)。

エントロピーの条件	ツリーおよびエントロピーのラベル付けに関する操作
$E (n o d e) \leq \sum_{c child of node} E o p t (c)$	node≠root であれば、結合して、Eopt(node) = E(node) と設定
$E (n o d e) > \sum_{c child of node} E o p t (c)$	分割して、 $E o p t (n o d e) = \sum_{c child of node} E o p t (c)$ と設定

ただし、参照ツリーの固有の初期条件として、各終端ノード t に対して Eopt(t) = E(t) とします。

ノードからの信号 Approximation の再構成

ライブスクリプトを開く

関数wprcoefを使用して、ウェーブレットパケットツリーの任意のノードから信号の Approximation を再構成できます。これは、作業にウェーブレットパケットツリー全体を使用しているか、最適性の基準で決定した部分木を使用しているかにかかわらず、当てはまります。信号の Approximation を再構成せずにノードからウェーブレットパケット係数を抽出するには、関数wpcoefを使用します。

ノイズがある Doppler 信号を読み込みます。現在の拡張モードを保存します。

load noisdopp
origMode = dwtmode("status","nodisp");

sym4 ウェーブレットを使用して、レベル 5 までウェーブレットパケット分解を計算します。周期化モードを使用します。ツリーをプロットします。

dwtmode("per","nodisp")
T = wpdec(noisdopp,5,"sym4");

ツリーをプロットし、(4,1) の組 (ノード 16) をクリックして、次のプロットを取得します。

関数 wpcoef を使用して、ノード 16 からウェーブレットパケット係数を抽出します。係数の長さを求めます。

wpc = wpcoef(T,16);
length(wpc)

ans = 64

関数 wprcoef を使用して、ノード 16 から信号の Approximation を求めます。Approximation の長さは元の信号の長さと等しくなります。

rwpc = wprcoef(T,16);
isequal(length(rwpc),length(noisdopp))

ans = logical
   1

Approximation と元の信号を比較します。

plot(noisdopp,"k")
hold on
plot(rwpc,"b",LineWidth=2)
axis tight
legend("Original","Approximation")
hold off

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Approximation.

最適なウェーブレットパケットの二分木を確認します。ツリーをプロットします。

Topt = besttree(T);
plot(Topt)

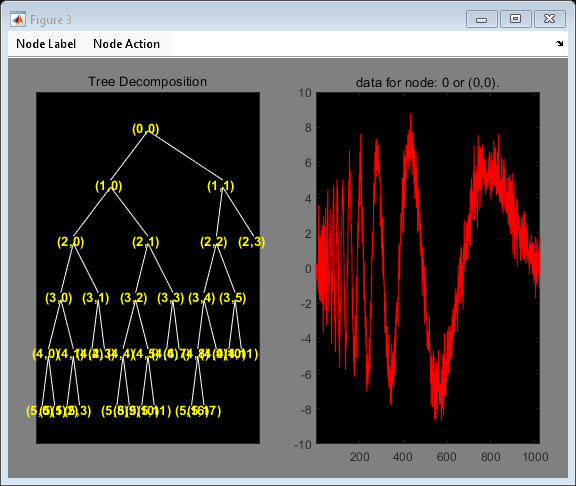
Figure contains 2 axes objects and other objects of type uimenu. Axes object 1 with title Tree Decomposition contains 69 objects of type line, text. Axes object 2 with title data for node: 0 or (0,0). contains an object of type line.

(3,0) の組 (ノード 17) をクリックした場合、次のプロットが表示されます。

(3,0) の組 (ノード 7) から信号の Approximation を再構成します。

rsig = wprcoef(Topt,7);
plot(noisdopp,"k")
hold on
plot(rsig,"b",LineWidth=2)
axis tight
legend("Original","Approximation")
hold off

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original, Approximation.

ウェーブレットパケットの二分木の中で抽出したい組がわかっている場合、関数depo2indを使用してその組に対応するノードを特定できます。(3,0) の組に対応するノードを判定します。

Node = depo2ind(2,[3 0])

Node = 7

拡張モードを元に戻します。

dwtmode(origMode,"nodisp")

2 次元ウェーブレットパケット分解構造

ウェーブレット分解の場合とまったく同様に、前述の 1 次元フレームワークはイメージ解析に拡張できます。わずかな変更を直接行うと、四分木に関する定義になります。深さ 2 の例を次の図に示します。

A quaternary tree of depth two. Each node has four sub nodes, except for the bottom level.

ウェーブレットパケットによる圧縮とノイズ除去

ウェーブレットパケットのフレームワークにおいて、圧縮とノイズ除去の考え方は、ウェーブレットのフレームワークで開発されたものと同じです。唯一新しい特徴は、より徹底的な解析によって柔軟性が向上することです。ウェーブレットパケットを使用した分解は 1 回で多数の基底を生成します。そこで、関数 besttree とエントロピー関数を使用して、設計目的に対して最適な表現を探すことができます。

参照

[1] Mallat, S. G., and Gabriel Peyré. A Wavelet Tour of Signal Processing: The Sparse Way. 3rd ed. Amsterdam: Elsevier/Academic Press, 2009.

[2] Coifman, R.R., and M.V. Wickerhauser. “Entropy-Based Algorithms for Best Basis Selection.” IEEE Transactions on Information Theory 38, no. 2 (March 1992): 713–18. https://doi.org/10.1109/18.119732.

ウェーブレット パケット

ウェーブレットからウェーブレット パケットへ

実際のウェーブレット パケット: はじめに

ウェーブレット パケットの作成

ウェーブレット パケットの原子

ウェーブレット パケットの構成

最適な分解の選択

興味深い部分木

ノードからの信号 Approximation の再構成

2 次元ウェーブレット パケット分解構造

ウェーブレット パケットによる圧縮とノイズ除去

参照

ウェーブレットパケット

ウェーブレットからウェーブレットパケットへ

実際のウェーブレットパケット: はじめに

ウェーブレットパケットの作成

ウェーブレットパケットの原子

ウェーブレットパケットの構成

2 次元ウェーブレットパケット分解構造

ウェーブレットパケットによる圧縮とノイズ除去