imodwt
Inverse maximal overlap discrete wavelet transform
Syntax
Description
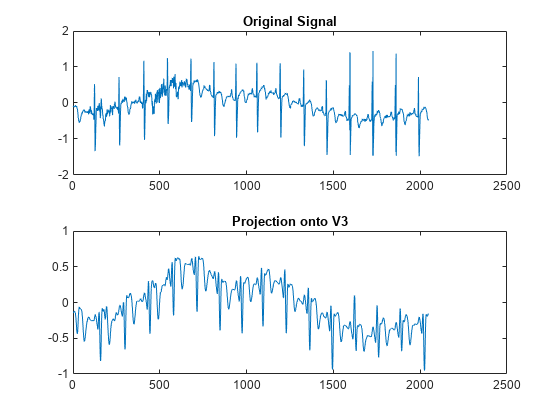
xrec = imodwt(w)w. By default, imodwt
assumes that you obtained w using the 'sym4'
wavelet with periodic boundary handling. If you do not modify the coefficients,
xrec is a perfect reconstruction of the signal.
xrec = imodwt(___,'reflection')'reflection', imodwt assumes
that the length of the original signal length is one half the number
of columns in the input coefficient matrix. By default, imodwt assumes
periodic signal extension at the boundary.
You must enter the entire character vector 'reflection'. If you
added a wavelet named 'reflection' using the wavelet manager, you
must rename that wavelet prior to using this option. 'reflection'
may be placed in any position in the input argument list after
x.
Examples
Input Arguments
Output Arguments
References
[1] Percival, Donald B., and Andrew T. Walden. Wavelet Methods for Time Series Analysis. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge ; New York: Cambridge University Press, 2000.
[2] Mesa, Hector. “Adapted Wavelets for Pattern Detection.” In Progress in Pattern Recognition, Image Analysis and Applications, edited by Alberto Sanfeliu and Manuel Lazo Cortés, 3773:933–44. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005. https://doi.org/10.1007/11578079_96.
Extended Capabilities
Version History
Introduced in R2015b