2-D FFT
Compute 2-D fast Fourier transform (FFT)
Libraries:
Computer Vision Toolbox /
Transforms
Description
The 2-D FFT block computes the discrete Fourier transform (DFT) of a two-dimensional input matrix using the fast Fourier transform (FFT) algorithm. The equation for the two-dimensional DFT F(m, n) of an M-by-N input matrix, f(x, y), is:
where and .
The block supports FFT implementation based on the FFTW library and an implementation based on a collection of Radix-2 algorithms. You can either manually select one of these implementations or let the block select one automatically.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
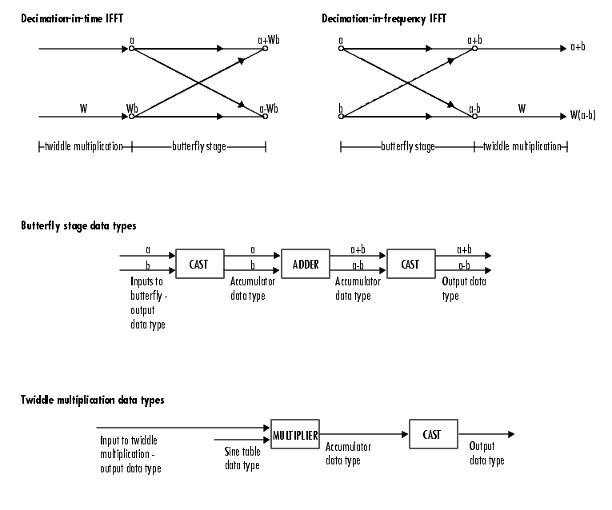
Algorithms
References
[1] “FFTW Home Page.” Accessed February 23, 2022. https://www.fftw.org/.
[2] Frigo, M., and S.G. Johnson. “FFTW: An Adaptive Software Architecture for the FFT.” In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP ’98 (Cat. No.98CH36181), 3:1381–84. Seattle, WA, USA: IEEE, 1998. https://doi.org/10.1109/ICASSP.1998.681704.
Extended Capabilities
Version History
Introduced before R2006a